特征向量与线性变换：揭秘矩阵背后的数学之美

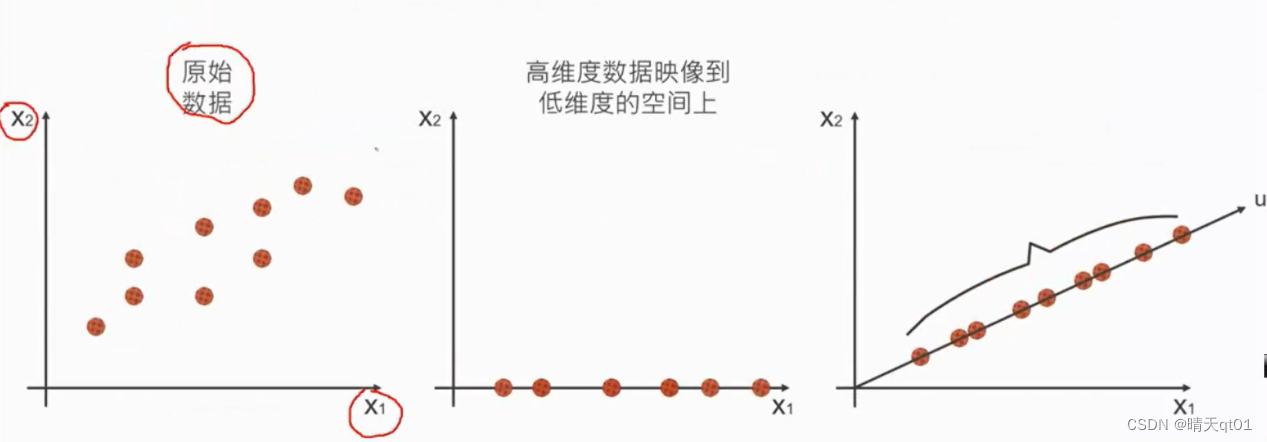
# 1. 特征向量与线性变换基础

特征向量是线性代数中一个重要的概念，它描述了线性变换如何影响向量。线性变换是将一个向量映射到另一个向量的函数，特征向量是线性变换下保持其方向不变的特殊向量。

特征值是与特征向量相关联的标量，它描述了线性变换如何改变特征向量的长度。特征值可以是实数或复数，正的特征值表示线性变换将特征向量拉伸，负的特征值表示线性变换将特征向量压缩。

# 2. 特征向量的理论与性质

### 2.1 特征向量的定义和几何意义

**定义：**

对于一个线性变换 T：V → V，如果存在一个非零向量 v ∈ V，使得 T(v) = λv，其中 λ 是一个标量，则称 v 为 T 的特征向量，λ 为 T 的特征值。

**几何意义：**

特征向量代表了线性变换在空间中的不变方向。当一个向量沿着特征向量方向变换时，其长度保持不变，仅方向发生改变。

### 2.2 特征值的计算方法和特征多项式

**特征值的计算方法：**

对于一个 n×n 矩阵 A，其特征值是多项式 det(A - λI) = 0 的根，其中 det 表示行列式，I 为单位矩阵。

**特征多项式：**

det(A - λI) = 0 被称为矩阵 A 的特征多项式。它的根就是矩阵 A 的特征值。

### 2.3 特征向量的正交性和线性无关性

**正交性：**

如果一个线性变换 T 有 n 个不同的特征值，则其对应的特征向量正交，即 v_i · v_j = 0，其中 i ≠ j。

**线性无关性：**

如果一个线性变换 T 有 n 个不同的特征值，则其对应的特征向量线性无关，即不存在非零标量 c_1, ..., c_n 使得 c_1v_1 + ... + c_nv_n = 0。

**代码示例：**

import numpy as np

# 定义一个矩阵 A
A = np.array([[2, 1], [-1, 2]])

# 计算特征值和特征向量
eig_vals, eig_vecs = np.linalg.eig(A)

# 打印特征值和特征向量
print("特征值：", eig_vals)
print("特征向量：", eig_vecs)

**代码逻辑分析：**

* `np.linalg.eig(A)` 函数计算矩阵 A 的特征值和特征向量。
* `eig_vals` 变量存储特征值，`eig_vecs` 变量存储特征向量。
* 特征值和特征向量分别对应于特征多项式 det(A - λI) = 0 的根和对应的向量。

**参数说明：**

* `A`：输入的 n×n 矩阵。
* `eig_vals`：输出的特征值列表。
* `eig_vecs`：输出的特征向量矩阵，每一列对应一个特征向量。

# 3.1 线性变换的矩阵表示

#### 线性变换的定义

线性变换，也称为线性映射，是将一个向量空间映射到另一个向量空间的函数，它满足以下两个性质：

1. **加法性：**对于向量空间 V 中的任意向量 x 和 y，以及标量 c，有 T(x + cy) = T(x) + cT(y)。
2. **齐次性：**对于向量空间 V 中的任意向量 x 和标量 c，有 T(cx) = cT(x)。

#### 矩阵表示

给定一个线性变换 T：V → W，其中 V 和 W 是有限维向量空间，我们可以使用矩阵来表示 T。选择 V 和 W 的基底，则 T 可以表示为一个 m × n 矩阵 A，其中 m 和 n 分别是 V 和 W 的维数。

矩阵 A 的元素 a_ij 表示当输入向量 v_j 时，输出向量 w_i 的第 j 个分量。也就是说，对于 V 中的任意向量 v，有 T(v) = Av。

#### 例子

考虑线性变换 T：R^2 → R^2，其作用是将向量旋转 90 度。选择基底 {(1, 0), (0, 1)}，则 T 的矩阵表示为：

A = | 0 -1 |
    | 1  0 |

因为当输入向量 (x, y) 时，输出向量为 (-y, x)。

### 3.2 矩阵的特征值分解定理

#### 特征值和特征向量

矩阵 A 的特征值 λ 是一个标量，使得存在非零向量 v，满足 Av = λv。向量 v 称为矩阵 A 对应于特征值 λ 的特征向量。

#### 特征值分解定理

特征值分解定理指出，对于任何 n × n 方阵 A，存在一个正交矩阵 P 和一个对角矩阵 D，使得 A = PDP^-1。其中：

* P 的列向量是 A 的 n 个特征向量。
* D 的对角线元素是 A 的 n 个特征值。

#### 几何意义

特征值分解的几何意义是将 A 的线性变换分解为一系列正交的拉伸或压缩变换。特征向量指定了这些变换的方向，而特征值指定了变换的幅度。

### 3.3 特征值分解的几何意义和应用

#### 几何意义

特征值分解的几何意义可以通过以下步骤理解：

1. 将矩阵 A 分解为 A = PDP^-1。
2. 矩阵 P 的列向量是 A 的特征向量，它们指定了 A 的线性变换的方向。
3. 矩阵 D 的对角线元素是 A 的特征值，它们指定了 A 的线性变换的幅度。
4. 对于 A 的任意输入向量 v，输出向量 Av 可以表示为：

Av = (PDP^-1)v = PD(P^-1v)

其中，P^-1v 是 v 在特征向量基底下的坐标。

#### 应用

特征值分解在许多应用中都有用，包括：

* **图像处理：**主成分分析（PCA）和图像压缩。
* **自然语言处理：**文本分类和文本聚类。
* **机器学习：**支持向量机（SVM）和降维技术（t-SNE）。
* **量子力学：**薛定谔方程的特征值问题和原子的能级和量子态。

# 4. 特征向量在应用中的实践

特征向量在图像处理、自然语言处理等领域有着广泛的应用。本章节将重点介绍特征向量在图像处理和自然语言处理中的具体实践。

### 4.1 特征向量在图像处理中的应用

#### 4.1.1 主成分分析（PCA）

主成分分析（PCA）是一种常用的降维技术，其原理是将原始数据投影到一个新的坐标系上，使得投影后的数据具有最大的方差。在图像处理中，PCA可以用于图像压缩和降噪。

**代码示例：**

import numpy as np
from sklearn.decomposition import PCA

# 加载图像数据
image = plt.imread('image.jpg')

# 将图像数据转换为一维数组
data = image.reshape(image.shape[0] * image.shape[1], 3)

# 进行PCA降维
pca = PCA(n_components=100)
data_pca = pca.fit_transform(data)

# 重构图像
image_reconstructed = data_pca.dot(pca.components_) + pca.mean_
image_reconstructed = image_reconstructed.reshape(image.shape[0], image.shape[1], 3)

# 显示原始图像和降维后的图像
plt.subplot(121)
plt.imshow(image)
plt.title('Original Image')

plt.subplot(122)
plt.imshow(image_reconstructed)
plt.title('Reconstructed Image')
plt.show()

**逻辑分析：**

* `reshape`函数将图像数据转换为一维数组，以便进行PCA降维。
* `PCA`类用于进行PCA降维，`n_components`参数指定降维后的主成分数。
* `fit_transform`方法将数据投影到主成分上，返回降维后的数据。
* `dot`方法用于将降维后的数据与主成分相乘，重构图像。
* `reshape`函数将重构后的数据转换为图像的原始形状。

#### 4.1.2 图像压缩

图像压缩是将图像数据进行编码，以便减少存储或传输所需的空间。特征向量可以用于图像压缩，原理是将图像投影到一个低维空间，然后只保存投影后的数据。

**代码示例：**

import numpy as np
from PIL import Image

# 加载图像数据
image = Image.open('image.jpg')

# 将图像数据转换为一维数组
data = np.array(image).reshape(image.size[0] * image.size[1], 3)

# 进行PCA降维
pca = PCA(n_components=100)
data_pca = pca.fit_transform(data)

# 保存降维后的数据
np.save('image_pca.npy', data_pca)

# 加载降维后的数据
data_pca = np.load('image_pca.npy')

# 重构图像
image_reconstructed = data_pca.dot(pca.components_) + pca.mean_
image_reconstructed = image_reconstructed.reshape(image.size[0], image.size[1], 3)

# 保存重构后的图像
Image.fromarray(image_reconstructed).save('image_compressed.jpg')

**逻辑分析：**

* `Image`类用于加载和保存图像。
* `reshape`函数将图像数据转换为一维数组。
* `PCA`类用于进行PCA降维，`n_components`参数指定降维后的主成分数。
* `fit_transform`方法将数据投影到主成分上，返回降维后的数据。
* `np.save`和`np.load`函数用于保存和加载降维后的数据。
* `dot`方法用于将降维后的数据与主成分相乘，重构图像。
* `reshape`函数将重构后的数据转换为图像的原始形状。
* `Image.fromarray`和`save`方法用于保存重构后的图像。

### 4.2 特征向量在自然语言处理中的应用

#### 4.2.1 文本分类

文本分类是将文本数据分配到预定义类别中的任务。特征向量可以用于文本分类，原理是将文本数据表示为一个向量，然后使用分类器对向量进行分类。

**代码示例：**

import numpy as np
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.linear_model import LogisticRegression

# 加载文本数据
data = ['This is a good movie.', 'This is a bad movie.', 'This is a neutral movie.']

# 将文本数据转换为特征向量
vectorizer = CountVectorizer()
X = vectorizer.fit_transform(data)

# 提取特征向量
features = vectorizer.get_feature_names_out()

# 构建分类器
classifier = LogisticRegression()

# 训练分类器
classifier.fit(X, [1, 0, 0])

# 预测文本类别
prediction = classifier.predict(['This is a good movie.'])
print(prediction)

**逻辑分析：**

* `CountVectorizer`类用于将文本数据转换为特征向量，`fit_transform`方法将文本数据转换为特征向量矩阵。
* `get_feature_names_out`方法提取特征向量中的特征名称。
* `LogisticRegression`类用于构建分类器，`fit`方法训练分类器。
* `predict`方法用于预测文本类别。

#### 4.2.2 文本聚类

文本聚类是将文本数据分组到相似组中的任务。特征向量可以用于文本聚类，原理是将文本数据表示为一个向量，然后使用聚类算法对向量进行聚类。

**代码示例：**

import numpy as np
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.cluster import KMeans

# 加载文本数据
data = ['This is a good movie.', 'This is a bad movie.', 'This is a neutral movie.']

# 将文本数据转换为特征向量
vectorizer = TfidfVectorizer()
X = vectorizer.fit_transform(data)

# 提取特征向量
features = vectorizer.get_feature_names_out()

# 构建聚类器
clusterer = KMeans(n_clusters=2)

# 聚类文本数据
clusterer.fit(X)

# 获取聚类标签
labels = clusterer.labels_
print(labels)

**逻辑分析：**

* `TfidfVectorizer`类用于将文本数据转换为特征向量，`fit_transform`方法将文本数据转换为特征向量矩阵。
* `get_feature_names_out`方法提取特征向量中的特征名称。
* `KMeans`类用于构建聚类器，`fit`方法聚类文本数据。
* `labels_`属性获取聚类标签。

# 5.1 特征向量在机器学习中的应用

### 5.1.1 支持向量机（SVM）

支持向量机（SVM）是一种强大的机器学习算法，用于分类和回归任务。它利用特征向量来将数据映射到高维空间，从而将非线性问题转换为线性问题。

#### SVM 的原理

SVM 的基本原理是找到一个超平面，该超平面将数据点正确地分为两类，同时最大化超平面与最近数据点的距离。这个超平面被称为**最大间隔超平面**。

#### 特征向量在 SVM 中的作用

在 SVM 中，特征向量用于将数据点映射到高维空间。这允许 SVM 处理非线性数据，因为在高维空间中，非线性关系可以表示为线性关系。

#### SVM 的代码示例

import numpy as np
from sklearn.svm import SVC

# 定义数据
X = np.array([[0, 0], [1, 1], [2, 2]])
y = np.array([0, 1, 0])

# 创建 SVM 分类器
clf = SVC()

# 训练 SVM
clf.fit(X, y)

# 预测新数据
new_data = np.array([[0.5, 0.5]])
prediction = clf.predict(new_data)

#### 代码逻辑分析

* `X` 和 `y` 分别表示数据点和对应的标签。
* `SVC()` 创建一个支持向量机分类器。
* `fit()` 方法训练 SVM，使用数据 `X` 和标签 `y`。
* `predict()` 方法使用训练好的 SVM 对新数据 `new_data` 进行预测。

### 5.1.2 降维技术（t-SNE）

t-SNE（t 分布随机邻域嵌入）是一种降维技术，用于将高维数据可视化到低维空间（通常为 2D 或 3D）。它利用特征向量来捕获数据中的局部和全局结构。

#### t-SNE 的原理

t-SNE 的原理是通过最小化高维空间和低维空间中数据点之间的差异来将数据映射到低维空间。它使用 t 分布来计算数据点之间的相似度，并使用随机邻域嵌入来保持数据点的局部结构。

#### 特征向量在 t-SNE 中的作用

在 t-SNE 中，特征向量用于将数据点映射到高维空间。这允许 t-SNE 处理复杂的数据，因为在高维空间中，数据点的相似性关系可以更好地表示。

#### t-SNE 的代码示例

import numpy as np
from sklearn.manifold import TSNE

# 定义数据
X = np.array([[0, 0], [1, 1], [2, 2], [3, 3], [4, 4]])

# 创建 t-SNE 模型
model = TSNE(n_components=2)

# 转换数据
transformed_data = model.fit_transform(X)

#### 代码逻辑分析

* `X` 表示高维数据。
* `TSNE()` 创建一个 t-SNE 模型，并将 `n_components` 设置为 2，表示将数据映射到 2D 空间。
* `fit_transform()` 方法将数据 `X` 转换为低维空间。

# 6. 奇异值分解（SVD）

奇异值分解（SVD）是特征值分解的一种推广，它适用于非方阵。SVD将一个矩阵分解为三个矩阵的乘积：

graph LR
subgraph SVD
    A[A] --> [U] --> U
    A[A] --> [S] --> S
    A[A] --> [V^T] --> V^T
end

其中：

- **A** 是待分解的矩阵。
- **U** 是一个正交矩阵，其列向量是 A 的左奇异向量。
- **S** 是一个对角矩阵，其对角线元素是 A 的奇异值。
- **V^T** 是一个正交矩阵，其行向量是 A 的右奇异向量。

奇异值分解的计算方法与特征值分解类似，可以使用奇异值分解算法或 SVD 函数库。

SVD 在许多应用中都有广泛的用途，包括：

- **图像处理：** 去噪、降维和图像压缩。
- **自然语言处理：** 文本分类、文本聚类和主题建模。
- **机器学习：** 降维、特征选择和推荐系统。
- **数据分析：** 数据可视化、异常检测和模式识别。