非线性回归模型应用案例：深入分析最佳实践

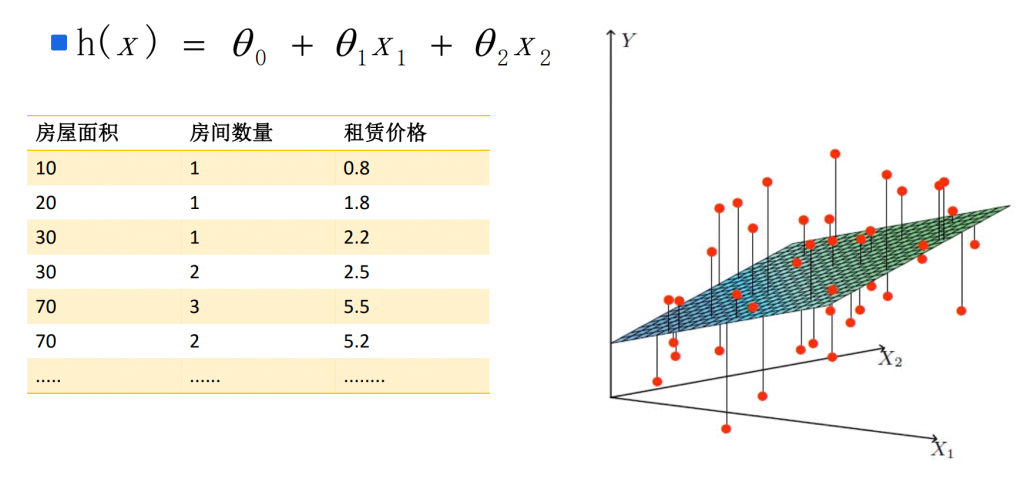
# 1. 非线性回归模型简介**

非线性回归模型是一种强大的统计建模技术，用于拟合具有非线性关系的数据。与线性回归模型不同，非线性回归模型允许因变量和自变量之间存在更复杂的函数关系。这使得非线性回归模型能够捕获现实世界中常见的复杂数据模式，例如指数增长、对数衰减和周期性行为。

非线性回归模型在广泛的领域中得到应用，包括金融预测、医疗诊断和工程设计。通过利用非线性关系，这些模型能够提供比线性模型更准确的预测和见解。

# 2. 非线性回归模型的理论基础

### 2.1 非线性回归模型的数学原理

#### 2.1.1 模型参数和假设

非线性回归模型的参数通常用向量 $\boldsymbol{\theta}$ 表示，其中每个元素 $\theta_i$ 对应模型中的一个参数。模型的假设通常包括：

- **线性相关性：** 响应变量 $y$ 和自变量 $\boldsymbol{x}$ 之间存在线性相关性，但这种相关性不是线性的。
- **误差项独立同分布：** 误差项 $\epsilon$ 服从独立同分布，即均值为 0，方差为 $\sigma^2$ 的正态分布。

#### 2.1.2 损失函数和优化算法

**损失函数**衡量模型预测值和真实值之间的差异，常见的损失函数有：

- **均方误差 (MSE)：** $L(\boldsymbol{\theta}) = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2$
- **绝对值误差 (MAE)：** $L(\boldsymbol{\theta}) = \frac{1}{n} \sum_{i=1}^n |y_i - \hat{y}_i|$

**优化算法**用于寻找使损失函数最小的参数 $\boldsymbol{\theta}$，常用的优化算法有：

- **梯度下降法：** 沿损失函数梯度的负方向迭代更新参数。
- **牛顿法：** 利用损失函数的海森矩阵进行迭代更新。

### 2.2 非线性回归模型的类型

#### 2.2.1 多项式回归

多项式回归模型将自变量 $x$ 提升到 $d$ 次幂，得到如下模型：

y = \beta_0 + \beta_1 x + \beta_2 x^2 + ... + \beta_d x^d + \epsilon

其中，$\beta_i$ 为模型参数。

#### 2.2.2 指数回归

指数回归模型采用指数函数对自变量进行变换，得到如下模型：

y = \alpha e^{\beta x} + \epsilon

其中，$\alpha$ 和 $\beta$ 为模型参数。

#### 2.2.3 对数回归

对数回归模型采用对数函数对自变量进行变换，得到如下模型：

y = \alpha + \beta \ln x + \epsilon

其中，$\alpha$ 和 $\beta$ 为模型参数。

# 3. 非线性回归模型