非线性回归模型评估指标解读与优化策略

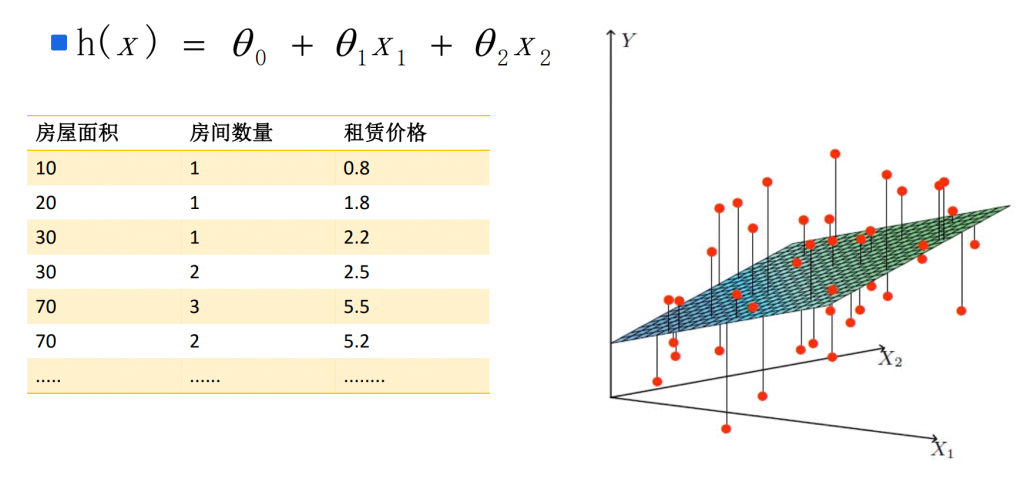
# 1. 非线性回归模型评估指标

非线性回归模型评估指标是衡量模型性能的关键指标，用于评估模型对非线性数据的拟合程度和预测准确性。常见的评估指标包括：

- **均方误差 (MSE)**：衡量预测值和真实值之间的平均平方误差。
- **均方根误差 (RMSE)**：MSE 的平方根，表示预测误差的标准差。
- **平均绝对误差 (MAE)**：衡量预测值和真实值之间的平均绝对误差。

# 2. 非线性回归模型评估指标优化策略

### 2.1 数据预处理优化

#### 2.1.1 数据归一化

**目的：**消除不同特征之间的量纲差异，提高模型训练效率和收敛速度。

**方法：**将原始数据映射到特定范围内，如 [0, 1] 或 [-1, 1]。

**代码块：**

import numpy as np

# 最小-最大归一化
data_normalized = (data - np.min(data)) / (np.max(data) - np.min(data))

# 标准化
data_normalized = (data - np.mean(data)) / np.std(data)

**逻辑分析：**

* 最小-最大归一化将数据映射到 [0, 1] 范围内，保留了原始数据的相对大小关系。
* 标准化将数据映射到均值为 0、标准差为 1 的范围内，消除了不同特征之间的差异性。

#### 2.1.2 特征工程

**目的：**提取和构造新的特征，提高模型的预测能力。

**方法：**

* **特征选择：**选择与目标变量相关性较高的特征。
* **特征转换：**通过数学运算或非线性映射将原始特征转换为新的特征。
* **特征组合：**将多个原始特征组合成新的特征。

**代码块：**

# 特征选择
from sklearn.feature_selection import SelectKBest, chi2

selector = SelectKBest(chi2, k=10)
selected_features = selector.fit_transform(X, y)

# 特征转换
from sklearn.preprocessing import PolynomialFeatures

transformer = PolynomialFeatures(degree=2)
transformed_features = transformer.fit_transform(X)

# 特征组合
from sklearn.preprocessing import OneHotEncoder

encoder = OneHotEncoder()
encoded_features = encoder.fit_transform(X)

**逻辑分析：**

* 特征选择消除了冗余和不相关的特征，提高了模型的泛化能力。
* 特征转换引入了非线性关系，增强了模型对复杂数据的拟合能力。
* 特征组合扩大了特征空间，增加了模型的表达能力。

### 2.2 模型选择优化

#### 2.2.1 模型选择准则

**目的：**选择最适合给定数据集和任务的模型。

**方法：**

* **交叉验证：**将数据集划分为训练集和测试集，多次训练和评估模型，计算平均性能。
* **信息准则：**AIC、BIC 等准则考虑模型复杂性和拟合程度，选择平衡二者的模型。
* **残差分析：**检查模型残差的分布和趋势，识别模型的不足之处。

**代码块：**

# 交叉验证
from sklearn.model_selection import cross_val_score

scores = cross_val_score(model, X, y, cv=5)

# 信息准则
from sklearn.metrics import r2_score

model_aic = AIC(r2_score(y, model.predict(X)))
model_bic = BIC(r2_score(y, model.predict(X)))

**逻辑分析：**

* 交叉验证提供了对模型泛化能力的无偏估计。
* 信息准则在模型复杂性和拟合程度之间进行权衡。
* 残差分析揭示了模型的偏差和方差，有助于进一步优化模型。

#### 2.2.2 超参数调优

**目的：**优化模型的超参数，提高模型的性能。

**方法：**

* **网格搜索：**在超参数空间中定义网格，遍历所有可能的超参数组合，选择最优组合。
* **随机搜索：**在超参数空间中随机采样，选择最优的超参数组合。
* **贝叶斯优化：**利用贝叶斯定理，在超参数空间中迭代搜索，逐步逼近最优组合。

**代码块：**

# 网格搜索
from sklearn.model_selection import GridSearchCV

param_grid = {'learning_rate': [0.01, 0.001, 0.0001], 'max_depth': [3, 5, 7]}
grid_search = GridSearchCV(model, param_grid, cv=5)
grid_search.fit(X, y)

# 随机搜索
from sklearn.model_selection import RandomizedSearchCV

param_distributions = {'learning_rate': [0.01, 0.001, 0.0001], 'max_depth': [3, 5, 7]}
random_search = RandomizedSearchCV(model, param_distributions, n_iter=10)
random_search.fit(X, y)

**逻辑分析：**

* 网格搜索提供了对超参数空间的全面搜索，但计算成本较高。
* 随机搜索在超参数空间中进行随机采样，计算成本较低，但可能错过最优组合。
* 贝叶斯优化利用历史搜索结果，逐步逼近最优组合，在计算成本和搜索效率之间取得平衡。

### 2.3 模型训练优化

#### 2.3.1 损失函数选择

**目的：**定义模型预测误差的度量标准，指导模型训练过程。

**方法：**

* **均方误差（MSE）：**衡量预测值与真实值之间的平方差。
* **平均绝对误差（MAE）：**衡量预测值与真实值之间的绝对差。
* **交叉熵损失：**用于分类任务，衡量预测概率分布与真实概率分布之间的差异。

**代码块：**

# 均方误差
from sklearn.metrics import mean_squared_error

mse = mean_squared_error(y, model.predict(X))

# 平均绝对误差
from sklearn.metrics import mean_absolute_error

mae = mean_absolute_error(y, model.predict(X))

# 交叉熵损失
from keras.losses import categorical_crossentropy

loss = categorical_crossentropy(y_true, model.predict(X))

**逻辑分析：**

* MSE 对异常值敏感，适合衡量连续变量的预测误差。
* MAE 对异常值不敏感，适合衡量离散变量的预测误差。
* 交叉熵损失用于分类任务，衡量模型对概率分布的预测能力。

#### 2.3.2 优化算法选择

**目的：**选择合适的优化算法，最小化损失函数，找到模型参数的最优值。

**方法：**

* **梯度下降：**沿损失函数梯度方向迭代更新模型参数。
* **动量法：**在梯度下降的基础上引入动量项，加速收敛速度。
* **RMSProp：**自适应学习率算法，根据梯度大小调整学习率。

**代码块：**

# 梯度下降
from keras.optimizers import SGD

optimizer = SGD(learning_rate=0.01)

# 动量法
from keras.optimizers import SGD

optimizer = SGD(learning_rate=0.01, momentum=0.9)

# RMSProp
from keras.optimizers import RMSprop

optimizer = RMSprop(learning_rate=0.001)

**逻辑分析：**

* 梯度下降是基本的优化算法，但可能收敛速度慢。
* 动量法通过动量项加速收敛，但可能导致振荡。
* RMSProp 自适应调整学习率，在收敛速度和稳定性之间取得平衡。

# 3.1 医学图像分析

在医学图像分析中，非线性回归模型评估指标被广泛用于评估图像分割、注册和分类任务的性能。

**图像分割：**
图像分割是将医学图像分割成具有不同解剖结构的区域。非线性回归模型评估指标，如 Dice 系数和交并比 (IoU)，用于量化分割结果与真实分割之间的相似性。这些指标考虑了分割区域的形状和大小，提供对分割准确性的全面评估。

**图像注册：**
图像注册是将两幅或多幅医学图像对齐的过程。非线性回归模型评估指标，如平均绝对误差 (MAE) 和均方根误差 (RMSE)，用于评估注册结果的准确性。这些指标衡量了对齐图像之间的像素差异，提供对图像对齐质量的定量评估。

**图像分类：**
图像分类是将医学图像分类到特定类别（例如，正常或异常）。非线性回归模型评估指标，如准确率、召回率和 F1 分数，用于评估分类模型的性能。这些指标考虑了模型正确预测和错误预测的样本数量，提供对分类准确性的全面评估。

### 3.2 金融预测

在金融预测中，非线性回归模型评估指标用于评估预测模型的性能，例如股票价格预测、汇率预测和经济增长预测。

**股票价格预测：**
股票价格预测模型使用非线性回归模型评估指标，如均方根误差 (RMSE) 和平均绝对误差 (MAE)，来评估预测价格与实际价格之间的差异。这些指标衡量了预测误差的幅度，提供对预测准确性的定量评估。

**汇率预测：**
汇率预测模型使用非线性回归模型评估指标，如对数似然函数和信息准则，来评估预测汇率与实际汇率之间的拟合程度。这些指标考虑了预测误差的分布和模型的复杂性，提供对预测性能的全面评估。

**经济增长预测：**
经济增长预测模型使用非线性回归模型评估指标，如平均绝对百分比误差 (MAPE) 和泰尔偏差，来评估预测经济增长率与实际增长率之间的差异。这些指标衡量了预测误差的相对大小，提供对预测准确性的定量评估。

### 3.3 时间序列预测

在时间序列预测中，非线性回归模型评估指标用于评估预测模型的性能，例如销售预测、需求预测和天气预测。

**销售预测：**
销售预测模型使用非线性回归模型评估指标，如平均绝对误差 (MAE) 和均方根误差 (RMSE)，来评估预测销售量与实际销售量之间的差异。这些指标衡量了预测误差的幅度，提供对预测准确性的定量评估。

**需求预测：**
需求预测模型使用非线性回归模型评估指标，如对数似然函数和信息准则，来评估预测需求与实际需求之间的拟合程度。这些指标考虑了预测误差的分布和模型的复杂性，提供对预测性能的全面评估。

**天气预测：**
天气预测模型使用非线性回归模型评估指标，如布里尔评分和根均方误差 (RMSE)，来评估预测天气条件与实际天气条件之间的差异。这些指标衡量了预测误差的概率和幅度，提供对预测准确性的定量评估。

# 4. 非线性回归模型评估指标的拓展与应用

### 4.1 多目标优化

在实际应用中，非线性回归模型的评估往往涉及多个目标，例如模型的准确性、鲁棒性和可解释性。多目标优化技术可以同时优化这些目标，从而获得更全面的模型评估结果。

**4.1.1 多目标优化算法**

常用的多目标优化算法包括：

- **加权和法：**将多个目标函数加权求和，形成一个单一的优化目标。
- **帕累托最优法：**寻找一组解，使得任何一个目标函数的改善都会导致另一个目标函数的恶化。
- **NSGA-II算法：**一种基于非支配排序的遗传算法，可以有效地求解多目标优化问题。

**4.1.2 多目标优化在非线性回归中的应用**

多目标优化可以用于非线性回归模型中，以同时优化模型的准确性、鲁棒性和可解释性。例如，可以通过以下步骤进行多目标优化：

1. 定义多个目标函数，例如均方根误差（MSE）、平均绝对误差（MAE）和模型复杂度。
2. 选择一个多目标优化算法，例如NSGA-II算法。
3. 运行优化算法，得到一组帕累托最优解。
4. 根据实际应用场景，从帕累托最优解中选择最合适的模型。

### 4.2 不确定性量化

非线性回归模型的预测往往存在不确定性，例如由于数据噪声、模型误差或参数估计的不确定性。不确定性量化技术可以量化和表征模型预测的不确定性。

**4.2.1 不确定性量化方法**

常用的不确定性量化方法包括：

- **蒙特卡罗方法：**通过多次随机采样，模拟模型预测的不确定性分布。
- **贝叶斯方法：**将模型参数视为随机变量，并使用贝叶斯推理来估计参数的后验分布。
- **区间分析：**使用区间算术来表征模型参数和预测的不确定性范围。

**4.2.2 不确定性量化在非线性回归中的应用**

不确定性量化可以用于非线性回归模型中，以评估模型预测的可靠性和鲁棒性。例如，可以通过以下步骤进行不确定性量化：

1. 选择一个不确定性量化方法，例如蒙特卡罗方法。
2. 对模型参数进行多次随机采样，得到模型预测的样本分布。
3. 分析样本分布，估计模型预测的不确定性范围和置信区间。
4. 根据不确定性量化结果，评估模型预测的可靠性和鲁棒性。

### 4.3 可解释性分析

非线性回归模型的预测往往具有较高的复杂度，难以直接理解和解释。可解释性分析技术可以帮助理解模型的预测过程和重要特征的影响。

**4.3.1 可解释性分析方法**

常用的可解释性分析方法包括：

- **特征重要性分析：**识别对模型预测影响最大的特征。
- **局部可解释模型可解释性（LIME）：**生成局部线性模型来解释单个预测。
- **SHAP值：**计算每个特征对模型预测的贡献度。

**4.3.2 可解释性分析在非线性回归中的应用**

可解释性分析可以用于非线性回归模型中，以增强模型的透明度和可信度。例如，可以通过以下步骤进行可解释性分析：

1. 选择一个可解释性分析方法，例如SHAP值。
2. 计算每个特征对模型预测的贡献度。
3. 可视化SHAP值，识别对模型预测影响最大的特征。
4. 根据可解释性分析结果，理解模型的预测过程和重要特征的影响。

# 5. 非线性回归模型评估指标的前沿研究与展望

非线性回归模型评估指标的研究领域不断发展，涌现出许多前沿的研究方向和应用前景。

### 多模态数据融合

随着数据采集技术的进步，多模态数据（例如图像、文本、音频）在现实世界中变得越来越普遍。非线性回归模型评估指标可以扩展到多模态数据融合，以提高模型在复杂数据上的性能。

### 因果推理

评估指标可以与因果推理技术相结合，以识别非线性回归模型中变量之间的因果关系。这对于理解模型行为和做出可靠的预测至关重要。

### 可解释性增强

可解释性是评估非线性回归模型的一个关键方面。前沿研究正在探索新的方法来增强模型的可解释性，例如通过可视化技术和基于注意力的方法。

### 鲁棒性提升

非线性回归模型容易受到异常值和噪声的影响。前沿研究致力于开发鲁棒的评估指标，以减轻这些影响并提高模型的稳定性。

### 实时评估

在某些应用中，需要对非线性回归模型进行实时评估。前沿研究正在开发轻量级且高效的评估指标，以满足这一需求。

### 领域特定应用

非线性回归模型评估指标在特定领域也得到了广泛的应用。例如，在医疗保健中，正在开发新的指标来评估疾病预测模型的性能。在金融中，指标被用于评估风险管理模型。

### 未来展望

非线性回归模型评估指标的研究领域将在未来继续蓬勃发展。随着新技术和应用的出现，预计将出现更多创新的指标和方法。通过持续的研究和创新，非线性回归模型评估指标将继续在各种领域发挥至关重要的作用，推动模型性能的提高和可靠预测的实现。