高斯过程回归：非线性回归的强大利器

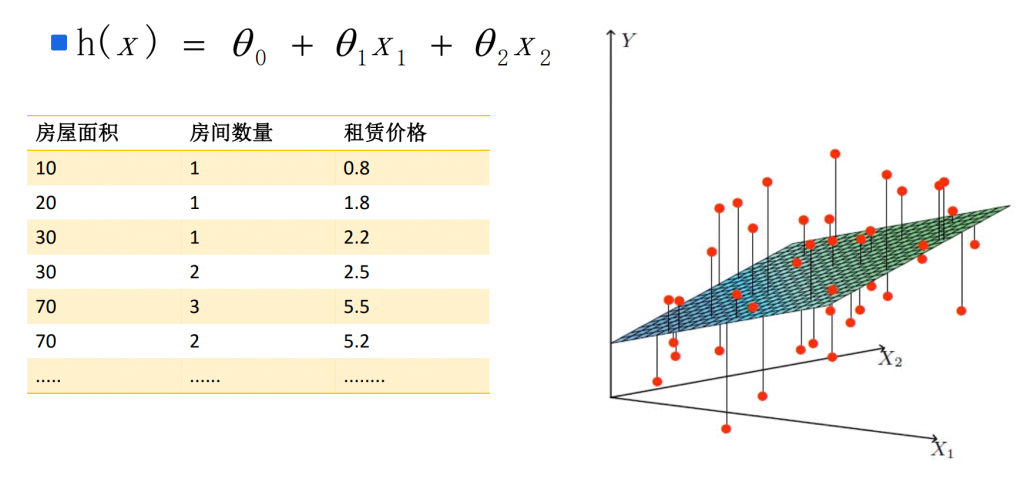
# 1. 高斯过程回归概述**

高斯过程回归（GPR）是一种强大的非线性回归技术，用于对复杂数据进行建模和预测。它基于高斯过程，这是一种随机过程，其中任何有限个点的联合分布都是多元正态分布。

GPR 模型假设输出是高斯过程的采样，该过程由均值函数和协方差函数定义。均值函数表示输出的预期值，协方差函数捕获输出之间的相关性。通过指定合适的协方差函数，GPR 可以适应各种非线性关系。

GPR 的优势在于其灵活性，它可以对各种数据类型进行建模，包括连续值、分类值和时间序列。此外，它提供了不确定性估计，这对于理解模型的预测能力至关重要。

# 2. 高斯过程回归理论

### 2.1 高斯过程的基本概念

高斯过程 (GP) 是一个随机过程，其中任何有限个点的联合分布都是多元正态分布。这意味着，GP 完全由其均值函数和协方差函数定义。

**均值函数**：指定 GP 的期望值。它可以是常数、线性函数或更复杂的非线性函数。

**协方差函数**：指定 GP 中任意两点之间的协方差。它定义了点之间的相关性，并决定了 GP 的平滑度和波动性。常用的协方差函数包括：

- 平方指数协方差函数：产生平滑的函数。
- 马特恩协方差函数：具有可调节的平滑度参数。
- 拉普拉斯协方差函数：产生尖锐的函数。

### 2.2 高斯过程回归模型

高斯过程回归 (GPR) 是一种非参数回归模型，它使用 GP 来对输入和输出变量之间的关系进行建模。GPR 模型由以下方程定义：

y = f(x) + ε

其中：

- `y` 是输出变量
- `x` 是输入变量
- `f(x)` 是 GP 确定的函数
- `ε` 是高斯噪声

GPR 模型假设 `f(x)` 是一个 GP，其均值函数和协方差函数已知。通过贝叶斯推断，我们可以估计 `f(x)` 的后验分布，并利用该分布进行预测。

### 2.3 推断和预测

在 GPR 中，推断涉及计算 `f(x)` 的后验分布。这可以通过使用以下公式完成：

p(f(x) | y, X) = N(μ(x), Σ(x, x))

其中：

- `p(f(x) | y, X)` 是 `f(x)` 的后验分布
- `μ(x)` 是后验均值
- `Σ(x, x)` 是后验协方差

一旦我们有了 `f(x)` 的后验分布，我们就可以使用它来预测新输入 `x*` 的输出。预测分布为：

p(y* | x*, y, X) = N(μ(x*), Σ(x*, x*))

其中：

- `p(y* | x*, y, X)` 是 `y*` 的预测分布
- `μ(x*)` 是预测均值
- `Σ(x*, x*)` 是预测协方差

# 3. 高斯过程回归实践

### 3.1 数据预