非线性回归模型最佳实践：总结经验教训，分享成功案例

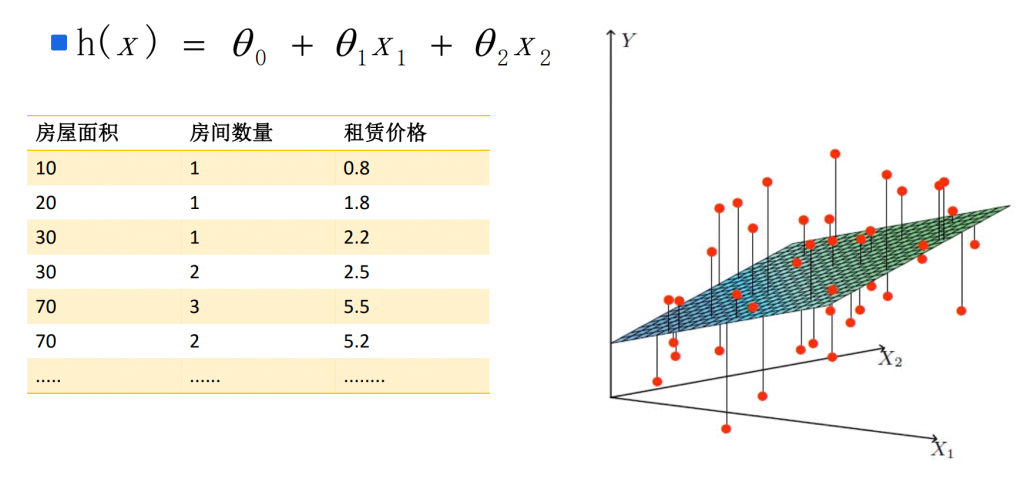
# 1. 非线性回归模型概述

非线性回归模型是一种统计模型，用于拟合非线性关系的数据。与线性回归模型不同，非线性回归模型假设因变量和自变量之间的关系是非线性的，即不能用一条直线来表示。

非线性回归模型在现实世界中有广泛的应用，因为它可以捕获复杂的数据模式，例如指数增长、衰减和周期性。这些模型在医疗、金融和制造业等领域特别有用，因为它们可以提供对复杂系统的深入了解。

本章将概述非线性回归模型的基本概念、类型和应用。我们将探讨这些模型的优点和局限性，并为理解和使用非线性回归模型奠定基础。

# 2. 非线性回归模型的理论基础

### 2.1 非线性模型的类型和特点

非线性模型是指模型中自变量和因变量之间的关系不是线性的。与线性模型相比，非线性模型具有以下特点：

- **复杂性：**非线性模型通常比线性模型更复杂，因为它们需要考虑自变量和因变量之间的非线性关系。
- **灵活性：**非线性模型可以拟合更广泛的数据类型，包括非线性、周期性或有界的数据。
- **解释性：**非线性模型可能更难解释，因为它们的自变量和因变量之间的关系可能不直观。

常见的非线性模型类型包括：

- **多项式回归：**将自变量提升到更高的幂次，从而产生非线性关系。
- **指数回归：**使用指数函数来建模自变量和因变量之间的关系。
- **对数回归：**使用对数函数来建模自变量和因变量之间的关系。
- **逻辑回归：**使用逻辑函数来建模自变量和因变量之间的关系，通常用于二分类问题。
- **神经网络：**使用多层感知器来建模复杂非线性关系。

### 2.2 非线性回归模型的拟合方法

拟合非线性回归模型的方法包括：

- **最小二乘法：**通过最小化误差平方和来估计模型参数。
- **最大似然估计：**通过最大化似然函数来估计模型参数。
- **贝叶斯方法：**使用贝叶斯定理来估计模型参数，考虑先验知识。

选择拟合方法取决于模型的复杂性、数据的类型和可用的计算资源。

**代码块：**

import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeatures

# 数据预处理
data = pd.DataFrame({'x': np.linspace(0, 10, 100), 'y': np.sin(np.linspace(0, 10, 100))})

# 线性回归
model_linear = LinearRegression()
model_linear.fit(data[['x']], data['y'])

# 多项式回归
model_poly = PolynomialFeatures(degree=2)
data_poly = model_poly.fit_transform(data[['x']])
model_poly = LinearRegression()
model_poly.fit(data_poly, data['y'])

# 拟合结果
print('线性回归：', model_linear.coef_, model_linear.intercept_)
print('多项式回归：', model_poly.coef_, model_poly.intercept_)

**逻辑分析：**

这段代码演示了线性回归和多项式回归的拟合过程。线性回归拟合一条直线，而多项式回归拟合一条二次曲线，以更好地拟合数据中的非线性关系。

**参数说明：**

- `LinearRegression()`：线性回归模型。
- `PolynomialFeat