【项目实战】：倒插法排序的应用案例与挑战

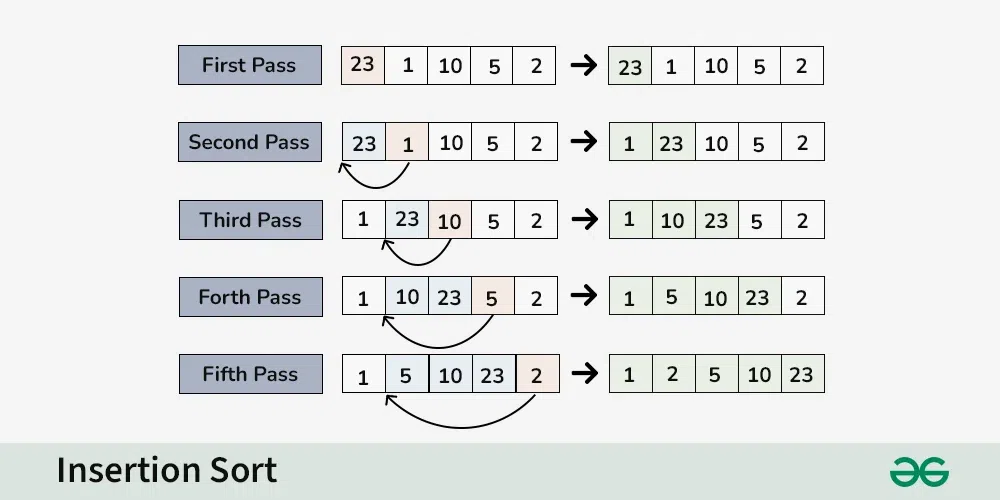
# 1. 倒插法排序算法概述

排序是计算机科学中一项基本且重要的操作，它涉及对一系列元素按照特定顺序重新排列。倒插法排序（Insertion Sort）作为一种简单直观的排序方法，特别适合处理较小的数据集。它的工作原理是将一个未排序的序列分成已排序和未排序两个部分，每次从未排序部分中取出一个元素插入到已排序序列的适当位置，直到所有元素都被正确排序。

## 2.1 排序算法的概念与重要性

排序算法是算法领域中的基础课题，它们在数据结构、数据库管理、计算机图形学及许多其他领域都有着广泛的应用。

### 2.1.1 排序的定义和分类

排序，顾名思义，就是将一组数据按照一定的顺序重新排列。数据可以按照数值大小、字典顺序或其他定义好的规则进行排序。常见的排序方式包括升序和降序。排序算法根据不同的标准，可以分为内部排序和外部排序，稳定排序和不稳定排序，比较排序和非比较排序等。

### 2.1.2 排序算法的性能评价标准

在选择排序算法时，我们需要考虑几个关键的性能指标：时间复杂度、空间复杂度和稳定性。时间复杂度决定了排序的执行时间，通常用大O表示法来描述最坏、平均和最好的情况。空间复杂度涉及到排序过程中需要使用的额外空间量。稳定性是指排序后，相同元素的相对顺序是否不变。

倒插法排序以其简洁的代码和稳定的性能，在许多实际应用中成为首选的排序方法，尤其是在数据量较小或者接近有序的情况下。在接下来的章节中，我们将详细探讨倒插法排序的工作原理、应用实践和性能优化策略。

# 2. 倒插法排序的理论基础

## 2.1 排序算法的概念与重要性

### 2.1.1 排序的定义和分类

在计算机科学中，排序是一种基本且核心的数据处理操作，旨在将一系列数据按照一定的顺序排列，可以是升序或降序。排序算法的分类多种多样，根据不同的标准可以划分为多种类别。例如，根据算法的比较操作，可以分为比较排序和非比较排序；根据时间复杂度，可以分为线性时间排序、对数时间排序和线性对数时间排序等。

在比较排序中，常见的算法有冒泡排序、选择排序、插入排序、快速排序、归并排序、堆排序等。这些算法都是基于比较元素间的大小来进行排序的。而在非比较排序中，比如计数排序、基数排序和桶排序，则更多地利用了数据的特性和分布来进行排序，它们在时间复杂度方面有时能够达到线性时间，即 O(n)，但对数据的要求较为严格。

### 2.1.2 排序算法的性能评价标准

排序算法的性能评价标准主要包括时间复杂度、空间复杂度和稳定性。时间复杂度是评价排序算法效率的主要指标，它决定了算法在处理大规模数据集时的性能表现。空间复杂度关注的是算法在执行过程中所需要的额外空间，它直接影响到算法是否能够在资源受限的环境中使用。稳定性是指排序算法在排序过程中是否能保持两个相等的元素的原始相对位置不变。

## 2.2 倒插法排序的工作原理

### 2.2.1 倒插法排序的基本步骤

倒插法排序（Insertion Sort）是一种简单直观的排序算法，基本思想是构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。算法的步骤如下：

1. 从第一个元素开始，该元素可以认为已经被排序。
2. 取下一个元素，在已经排序的元素序列中从后向前扫描。
3. 如果该元素（已排序）大于新元素，将该元素移到下一位置。
4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置。
5. 将新元素插入到该位置后。
6. 重复步骤1~5。

### 2.2.2 算法的时空复杂度分析

倒插法排序的平均时间复杂度和最坏时间复杂度均为 O(n^2)，这在排序算法中是效率较低的一种。然而，倒插法排序也有其优点，特别是当数据接近排序状态时，其性能接近 O(n)。空间复杂度方面，倒插法排序是原地排序算法，即不需要额外的存储空间，所以空间复杂度为 O(1)。

## 2.3 倒插法排序与其他排序算法的比较

### 2.3.1 常见排序算法的对比

在常见的排序算法中，冒泡排序和选择排序都具有和倒插法排序相同的 O(n^2) 最坏时间复杂度，但冒泡排序通常比倒插法排序有更少的交换操作。快速排序在平均情况下具有 O(nlogn) 的时间复杂度，是非常高效的排序算法，但它在最坏情况下的时间复杂度可达到 O(n^2)。归并排序在所有情况下都能保证 O(nlogn) 的时间复杂度，并且是稳定的排序算法。堆排序同样有 O(nlogn) 的时间复杂度，但不具有稳定性。

### 2.3.2 倒插法排序的优势与局限性

倒插法排序的优势在于算法简单、易于实现且在数据量不大时效率较高。它对小规模数据集非常有效，尤其是在数据量接近排序状态时。其局限性在于当处理大规模数据时，时间复杂度较高，不适合应用于复杂度要求高的场景。此外，倒插法排序不是稳定的排序算法，在需要保持相等元素相对顺序的场景中不适用。

# 3. 倒插法排序实践应用

在当今数据驱动的世界中，排序技术无处不在，而倒插法排序在数据处理、编程和实际项目中都扮演着重要角色。本章将探讨倒插法排序的实际应用，包括在数据处理中的应用、在不同编程语言中的实现，以及实际项目案例的深入分析。

## 3.1 倒插法排序在数据处理中的应用

倒插法排序算法在数据处理领域中的应用广泛，特别是在数据清洗、预处理和分析挖掘中。由于其简洁和易于实现的特点，倒插法排序为数据科学家和工程师提供了一种高效的方法来组织和处理数据。

### 3.1.1 数据清洗与预处理

在数据清洗与预处理阶段，我们需要对数据进行排序以确保数据的顺序性。例如，在准备数据进行统计分析之前，可能需要按照时间戳或标识符排序以消除重复记录或错误。倒插法排序由于其简单的逻辑，能够快速地处理这类问题。

#### 示例代码：

def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key
    return arr

# 示例：对一个包含时间戳的列表进行排序
timestamps = [***, ***, ***]
sorted_timestamps = insertion_sort(timestamps)
print(sorted_timestamps)

#### 参数说明及逻辑分析：

- `arr`：传入一个需要排序的列表。
- `for i in range(1, len(arr))`：外层循环从列表的第二个元素开始遍历，因为它默认第一个元素已经是排序好的。
- `key = arr[i]`：定义当前遍历到的元素为key。
- `j = i - 1`：定义一个变量j，初始值为i-1。
- `while j >= 0 and key < arr[j]`：内层循环寻找key值的正确位置，条件是如果key小于它前面的元素且j大于等于0。
- `arr[j + 1] = arr[j]`：将比key大的元素向后移动一位。
- `arr[j + 1] = key`：找到key的正确位置后，将它插入。
- 代码返回排序后的列表。

通过上述代码，我们可将未排序的时间戳列表转换为有序列表，这在数据清洗过程中是常见的操作。

### 3.1.2 数据分析与挖掘中的排序实现

在数据分析与挖掘任务中，数据通常需要按照特定的特征进行排序。例如，对客户购买行为数据按照购买金额从高到低排序，可以帮助我们识别出消费能力最强的客户。

#### 代码块：

def sort_by_value(data, key):
    return sorted(data, key=lambda item: item[key], reverse=True)

# 示例：根据金额排序客户数据
customer_data = [
    {'name': 'Alice', 'purchase': 120.50},
    {'name': 'Bob', 'purchase': 230.25},
    {'name': 'Charlie', 'purchase': 99.75}
]
sorted_customers = sort_by_value(customer_data, 'purchase')
print(sorted_customers)