【算法极限挑战】：倒插法排序的时间与空间复杂度分析

# 1. 倒插法排序概述

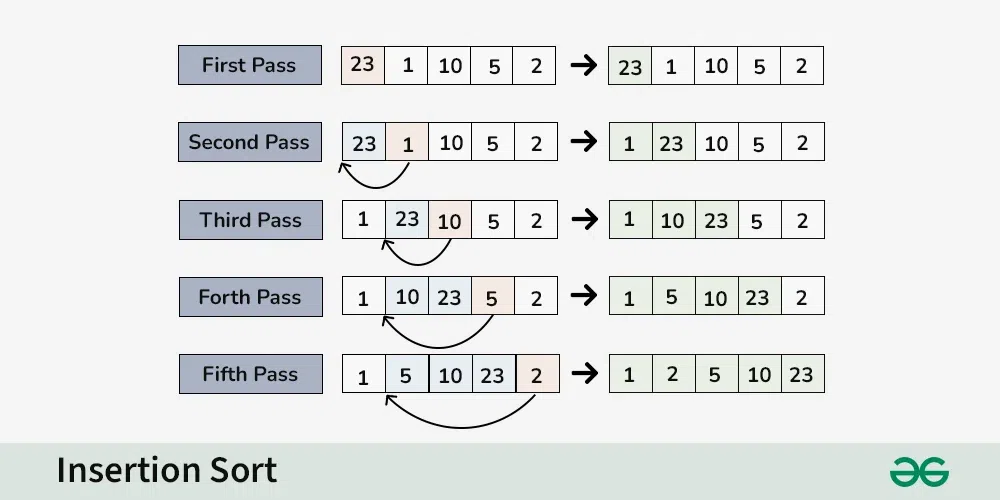
倒插法排序（也称为插入排序的一种变体）是一种简单直观的排序算法，尤其适合小规模数据集的排序。它的工作原理类似于我们整理牌的过程：从左到右，逐步将每张牌插入到已排序序列的合适位置上。虽然它的平均和最坏情况时间复杂度均为O(n^2)，但在实际应用中，对于部分或几乎已经排好序的数据集，倒插法排序的效率会很高。

## 2.1 倒插法排序的基本原理
### 2.1.1 排序算法的定义和目标
排序算法旨在按照特定顺序重新排列一组数据。其核心目标是将输入的序列，经过一系列操作后达到有序状态。对于倒插法排序而言，目标是构建一个有序序列，使得每个元素都处于其最终位置上。

### 2.1.2 倒插法排序的工作机制
该算法通过以下步骤工作：
1. 从数组的第二个元素开始，认为这个元素是“当前元素”。
2. 将“当前元素”与其左侧已排序的元素进行比较。
3. 如果左侧元素大于“当前元素”，则将左侧元素向右移动一位。
4. 重复步骤2和3，直到找到“当前元素”的合适位置并将其插入。
5. 继续选择下一个元素作为“当前元素”，重复以上步骤直到所有元素都被排序。

尽管倒插法排序在理论上可能不是最高效的选择，但在特定条件下，它能够提供比其他复杂算法更快的排序速度，比如在数据几乎已排序的情况下。此外，它还易于理解和实现，是一种教学和理解基础排序原理的优秀算法。

# 2. 理论分析

### 倒插法排序的基本原理

#### 排序算法的定义和目标
排序算法是计算机科学中的一项基本操作，其目的是将一系列数据元素按照特定的顺序（通常是从小到大或者从大到小）进行排列。排序算法的效率直接影响到程序的性能，特别是在需要处理大量数据时。排序的基本目标是高效地将无序的数据转变为有序，同时尽可能减少所需的时间和空间资源。

#### 倒插法排序的工作机制
倒插法排序（Insertion Sort）是一种简单直观的排序算法，其工作原理是构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。具体步骤为：

1. 从第一个元素开始，该元素可以认为已经被排序。
2. 取出下一个元素，在已经排序的元素序列中从后向前扫描。
3. 如果该元素（已排序）大于新元素，将该元素移到下一位置。
4. 重复步骤3，直到找到已排序的元素小于或者等于新元素的位置。
5. 将新元素插入到该位置后。
6. 重复步骤2~5。

### 时间复杂度分析

#### 最佳、平均和最坏情况分析
时间复杂度是衡量排序算法性能的重要指标之一，它描述了算法执行所需的操作数与输入规模的关系。对于倒插法排序而言：

- **最佳情况**（Best Case）：输入数据已经是正序的情况下，只需要进行一次比较即可完成排序，因此时间复杂度为 O(n)。
- **平均情况**（Average Case）：输入数据随机排列时，平均每次插入都要比较一半的数据，因此时间复杂度为 O(n^2)。
- **最坏情况**（Worst Case）：输入数据为逆序时，每次插入都需要与所有已排序的元素进行比较，因此时间复杂度为 O(n^2)。

#### 时间复杂度的数学推导
通过数学推导可以更精确地了解倒插法排序的时间复杂度。考虑一个有 n 个元素的数组，倒插法排序需要进行的比较次数 C(n) 可以通过以下方式推导：

C(n) = (n-1) + (n-2) + ... + 1
     = n(n-1)/2
     = O(n^2)

### 空间复杂度分析

#### 空间复杂度的定义和计算
空间复杂度是表示排序算法在执行过程中临时占用存储空间的大小。对于倒插法排序，它不需要额外的存储空间，所有的排序过程都在原数组上进行，因此空间复杂度为 O(1)。也就是说，倒插法排序是一个原地排序算法。

#### 倒插法排序的空间占用特点
由于倒插法排序不需要开辟额外的数组或内存空间，这一点让它在空间资源紧张的情况下表现出色。但是，由于其排序过程是在原数组上进行，这限制了排序的稳定性。对于已经排序好的元素，倒插法排序可能会导致它们的相对位置发生变化，因此它不是一个稳定的排序算法。

在下一章节中，我们将更深入地探讨倒插法排序的实践演练，包括编程语言的选择、环境搭建、代码实现以及如何进行实例验证和性能测试。我们将通过具体的编程实例来展示倒插法排序的应用，以及如何在实际开发中应用这种排序方法。

# 3. 实践演练

## 3.1 编程语言的选择和环境搭建
### 3.1.1 语言特性对比
在选择实现倒插法排序的编程语言时，需要考虑语言的性能、易用性、以及社区支持等因素。一些流行的语言如Python、Java和C++都有各自的优势：

- **Python**：语法简洁，易于学习和实现，拥有强大的标准库和第三方库支持。但Python解释型语言的本质，意味着它的执行效率不如编译型语言。
- **Java**：具有跨平台特性和良好的标准库支持。Java是半编译半解释的语言，相对Python来说，在性能上有一定优势。
- **C++**：接近硬件层，编译后执行速度极快，非常适合性能要求高的场景。C++的复杂性也意味着编码和调试的难度较高。

根据这些特性，我们可以选择适合的编程语言来实现倒插法排序。对于追求性能的场景，C++是更好的选择；而对于快速原型开发，Python则更为合适。

### 3.1.2 开发环境的配置
在选定编程语言后，接下来需要配置一个合适的开发环境：

- **Python**：安装Python解释器和一个简单的文本编辑器，如VS Code、PyCharm或者直接使用Jupyter Notebook。
- **Java**：安装Java Development Kit (JDK) 并配置环境变量，同时安装如IntelliJ IDEA或Eclipse这类集成开发环境 (IDE)。
- **C++**：安装一个支持C++的IDE，例如Visual Studio或Code::Blocks，并确保安装了适合的编译器。

为了确保开发环境的稳定性，建议使用虚拟环境或容器技术，比如Python的`venv`模块，Java的Maven或Gradle构建系统，以及C++的`CMake`构建工具。

## 3.2 倒插法排序的代码实现
### 3.2.1 排序算法的编码步骤
为了实现倒插法排序，首先需要理解其基本原理：从数组的末尾开始，比较相邻的两个元素，如果顺序错误就交换它们的位置。重复这个过程，直到没有需要交换的元素为止。

以下是使用C++实现倒插法排序的基本步骤：

1. **初始化数组**：首先定义一个待排序的数组。
2. **遍历数组**：从数组的第二个元素开始向前遍历。
3. **比较与交换**：对于每个元素，与它之前的所有元素进行比较，如果发现逆序，就交换这两个元素的位置。
4. **重复步骤**：直到整个数组按非递减顺序排列。

### 3.2.2 关键代码解释
下面是C++语言实现倒插法排序的关键代码段：

#include <iostream>
using namespace std;

void insertionSort(int arr[], int n) {
    int i, key, j;
    for (i = 1; i < n; i++) {
        key = arr[i];
        j = i - 1;

        // 将大于key的元素向后移动一个位置
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key;
    }
}

int main() {
    int arr[] = {64, 34, 25, 12, 22, 11, 90};
    int n = sizeof(arr)/sizeof(arr[0]);
    insertionSort(arr, n);
    for (int i = 0; i < n; i++)
        cout << arr[i] << " ";
    cout << endl;
    return 0;
}

- **`insertionSort`函数**：实现倒插法排序算法的主要逻辑。
-