【倒插法排序变种探究】：不同场景下的最优解揭秘

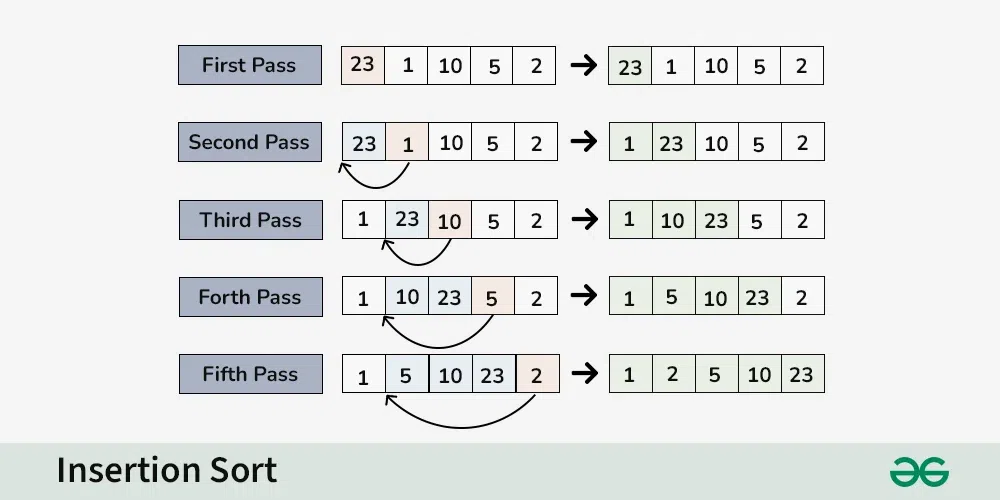
# 1. 倒插法排序的基本原理

排序是计算机科学中的一个基础概念，涉及按照特定顺序重新排列一系列元素。倒插法排序，又名插入排序，是一种直观且易于实现的排序算法。其基本思想是将一个数据序列划分为已排序和未排序两部分，每一次从未排序的部分取出一个元素，将其插入到已排序部分的适当位置，最终使得整个数据序列变成有序状态。

以数组 [5, 2, 9, 1, 5, 6] 为例，倒插法排序的过程大致如下：

1. 从第二个元素开始，将2插入到[5]中，序列变为 [2, 5, 9, 1, 5, 6]
2. 接着将9插入到[2, 5]中，序列保持不变 [2, 5, 9, 1, 5, 6]
3. 将1插入到[2, 5, 9]中，序列变为 [1, 2, 5, 9, 5, 6]
4. 将5插入到[1, 2, 5, 9]中，序列变为 [1, 2, 5, 5, 9, 6]
5. 最后将6插入到[1, 2, 5, 5, 9]中，最终序列变为 [1, 2, 5, 5, 6, 9]

倒插法排序的优点在于它简单易懂，且在数据集较小或者数据已经部分有序的情况下具有较高的效率。然而，对于大规模数据集，其性能会显著下降。因此，理解倒插法排序的基本原理，对于选择合适的排序策略和优化算法性能至关重要。

# 2. 倒插法排序在不同数据集上的表现

## 2.1 倒插法排序在小型数据集上的效率分析

### 2.1.1 小型数据集的特点及其对排序算法的影响

小型数据集通常包含较少数量的元素，这意味着算法的运行时间不会受到大量数据处理的显著影响。由于数据规模有限，排序算法在小型数据集上的效率更多地取决于单个操作的性能，比如元素比较和交换次数。在这种情况下，算法的时间复杂度不一定是评估效率的主要因素，因为即便是复杂度较高的算法在小型数据集上也可能表现出色。

### 2.1.2 倒插法排序与其他算法在小型数据集上的对比

在小型数据集上，倒插法排序可能与快速排序和归并排序等算法竞争。由于倒插法排序的平均时间复杂度为O(n^2)，理论上它在小型数据集上的表现不会优于时间复杂度为O(n log n)的算法。然而，在实际测试中，倒插法排序的简单性和实现的高效性使得它在元素数量非常少时可以迅速完成排序任务。

为了具体比较倒插法排序与其他算法的效率，可以设计一个实验，分别在不同的小型数据集上运行倒插法排序和如插入排序、选择排序等简单排序算法，记录每种算法的执行时间和资源消耗。通过实验数据，我们可以得到更为直观的效率对比。

## 2.2 倒插法排序在大型数据集上的效率分析

### 2.2.1 大型数据集的特点及其对排序算法的影响

与小型数据集相比，大型数据集的排序需要考虑算法的时间和空间复杂度。时间复杂度在大型数据集上显得尤为重要，因为O(n^2)的算法会随着数据量的增加而显著降低效率。此外，数据的读写操作也会成为性能瓶颈，因为它们通常比内存操作要慢得多。

### 2.2.2 倒插法排序与其他算法在大型数据集上的对比

倒插法排序在大型数据集上的性能通常不如时间复杂度为O(n log n)的排序算法。但是，倒插法排序在某些特定环境下仍有可能被采用。例如，在排序已经部分有序的数据集时，倒插法排序可以因为其较少的交换操作而显示出较好的性能。

为了对比倒插法排序和其他算法在大型数据集上的表现，可以通过编写程序来对不同数量级的数据集进行排序，并记录每种算法的执行时间、内存使用等指标。实验结果可以使用表格或者图表来展示，以此揭示不同算法在不同数据规模下的效率表现。

在这些分析中，可以使用伪代码或者流程图来描述算法的执行过程，以便更清晰地展示排序算法在数据集上的操作。下图是一个简单的倒插法排序流程图：

graph TD
    A[开始] --> B[初始化数组]
    B --> C{数组是否已排序}
    C -- 是 --> Z[结束]
    C -- 否 --> D[从第二个元素开始，将当前元素与之前的元素比较]
    D --> E{当前元素是否小于之前的元素}
    E -- 是 --> F[将之前的元素向后移动]
    E -- 否 --> G[将当前元素放到正确的位置]
    F --> H[继续向前比较]
    G --> C
    H --> D

倒插法排序的伪代码如下：

倒插法排序(数组 A)
    对于 i = 1 到 A.length-1
        临时变量 temp = A[i]
        j = i
        // 将 A[i] 向前移动到正确的位置
        在 A[j-1] > temp 时重复
            A[j] = A[j-1]
            j = j - 1
        结束循环
        A[j] = temp
    结束循环

通过这样的实验分析和图表描述，我们可以更深入地理解倒插法排序在不同数据集上的表现，并能够为特定应用场景下算法的选择提供依据。

# 3. 倒插法排序的时间复杂度和空间复杂度

## 3.1 倒插法排序的时间复杂度分析

### 3.1.1 最佳情况、平均情况和最坏情况的时间复杂度

倒插法排序（Insertion Sort）是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。时间复杂度是衡量算法执行时间与输入数据大小关系的重要指标。

- **最佳情况**：对于一个已经排好序的数组进行倒插法排序，算法只需要进行比较操作，不需要移动元素。因此，最佳情况的时间复杂度为O(n)。
- **平均情况**：对于随机分布的数据集，每次插入平均需要比较一半的数据并移动一半的数据，所以平均情况的时间复杂度为O(n^2)。

- **最坏情况**：对于逆序的数据集，每次插入都需要比较所有已排序的数据并移动这些数据，最坏情况的时间复杂度也为O(n^2)。

### 3.1.2 时间复杂度的理论推导和实验验证

时间复杂度的理论推导主要依据算法中循环的次数。在倒插法排序中，最外层循环为 n-1 次（因为第一个元素默认已经排序），内层循环依赖于当前插入元素与已排序部分的比较，其次数变化较大，但平均情况下可以认为是 n/2 次。

进行实验验证的一个方法是编写代码，对不同大小和不同特征的数据集进行排序，并记录算法执行时间。然后通过绘制数据图表，比较理论预测与实验结果是否一致。

#include <stdio.h>
#include <stdlib.h>
#include <time.h>

void insertionSort(int arr[], int n) {
    int i, key, j;
    for (i = 1; i < n; i++) {
        key = arr[i];
        j = i - 1;
        while (j >= 0 && arr[j] > key) {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key;