【多维数据排序】：倒插法排序扩展技巧与应用

# 1. 多维数据排序的理论基础

在处理多维数据时，排序作为基础且关键的操作，直接关系到数据处理的效率和结果的准确性。本章将深入探讨多维数据排序的理论基础，揭示排序算法的内核，以及在多维数据场景下实现高效排序的必要性。

## 1.1 数据排序的重要性

在任何数据密集型的应用中，排序不仅仅是数据展示的需要，更是数据检索、存储优化和后续复杂分析的前提。特别是对于多维数据，如矩阵、数组、数据库中的多列数据，排序的策略和效率将直接影响到数据处理的性能。

## 1.2 排序算法的基本分类

根据不同的使用场景和数据特性，排序算法可以分为比较排序和非比较排序两大类。比较排序依赖于元素间的比较操作，如快速排序、归并排序等；而非比较排序不直接比较元素大小，利用元素的某些特性进行排序，如计数排序、基数排序等。了解这些分类对于正确选择和优化排序算法至关重要。

## 1.3 多维数据排序的挑战

多维数据排序不同于单维数据，因为它涉及到多个排序键（key），每个维度可能有不同的排序标准。这使得多维数据排序更为复杂。在设计排序算法时，我们需要考虑如何高效地管理多维度的排序顺序以及如何保持数据的关联性，这对于算法的实现和优化提出了更高的要求。

# 2. 倒插法排序的原理与实践

## 2.1 倒插法排序的基本概念

### 2.1.1 排序算法概述

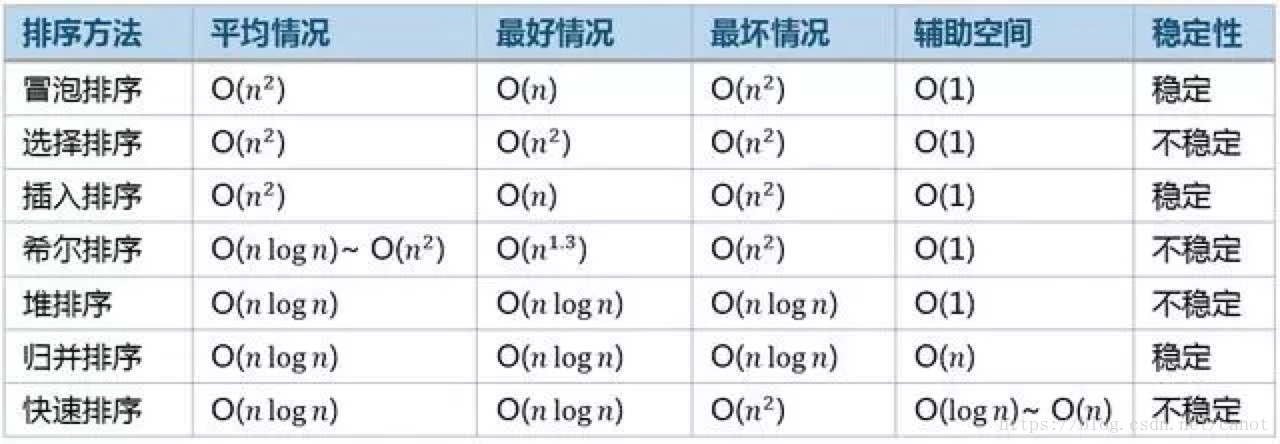
排序算法是编程中一种常见且关键的操作，它将一系列数据按照一定的顺序（升序或降序）进行排列。排序算法的效率直接影响到程序的运行速度和资源消耗。在不同的应用场景下，选择合适的排序算法至关重要。常见的排序算法包括冒泡排序、选择排序、插入排序、快速排序、归并排序等。这些算法各有优劣，适用于不同的数据规模和场合。

### 2.1.2 倒插法排序定义与特性

倒插法排序（也称为插入排序的一种变体）是一种简单直观的排序方法。它通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。倒插法排序适用于小规模数据集，因为其简单易于实现且在最坏情况下仍有不错的性能表现。

## 2.2 倒插法排序算法实现

### 2.2.1 单维数组排序

在单维数组排序中，倒插法排序算法通过在已排序数组中找到正确位置将新元素插入。下面给出一个倒插法排序的实现示例：

def reverse_insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        # 将arr[i]插入到已排序的arr[0...i-1]中
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key
    return arr

### 2.2.2 多维数组排序

多维数组排序稍微复杂，需要定义排序的基准维度。例如，若有一个二维数组，我们可以按照数组中的一列来对整个数组进行排序。这里提供一个按第一列排序的二维数组示例：

def reverse_insertion_sort_2d(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        while j >= 0 and key[0] < arr[j][0]:
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key
    return arr

### 2.2.3 关键代码分析

在关键代码中，我们首先定义了待排序的数组，然后通过一个循环，从第二个元素开始，依次将当前元素与其前面已排序的元素进行比较。如果当前元素小于前面的元素，则将前面的元素后移一位，直到找到正确的位置插入当前元素。值得注意的是，这种方法的性能依赖于元素之间的相对大小和数据的初始排列状态。在最好的情况下，如果数据已经部分有序，倒插法排序的性能可以接近 O(n)。

## 2.3 倒插法排序的性能评估

### 2.3.1 时间复杂度分析

倒插法排序的最坏时间复杂度为 O(n^2)，这是当数组完全逆序时的情况。最好的时间复杂度为 O(n)，这发生在数组已经完全有序的情况下。平均时间复杂度也为 O(n^2)，因为对于随机数组，每次插入都需要进行大约 n/2 次比较和移动。

### 2.3.2 空间复杂度分析

倒插法排序是一个原地排序算法，它不需要额外的存储空间，因此空间复杂度为 O(1)。这意味着倒插法排序在空间使用上是非常高效的。

### 2.3.3 实际应用场景对比

尽管倒插法排序在最坏情况下的时间复杂度较高，但在小规模数据集或部分有序的数据集中，其性能往往优于更复杂的排序算法，如快速排序或归并排序。对于实际应用场景，建议在数据量不大或有部分有序性质时优先考虑倒插法排序。

在下一章节中，我们将探讨多维数据排序的扩展技巧，并通过具体案例进一步加深理解。

# 3. 多维数据排序的扩展技巧

## 3.1 排序算法的创新与改进
### 3.1.1 算法优化方法

在处理多维数据排序问题时，我们通常采用多种策略来提高算法的效率和优化性能。这些策略包括但不限于以下几点：

- **启发式搜索**：利用特定领域知识减少搜索空间，如使用特定的排序顺序或偏好的排序规则。
- **自适应排序**：根据数据的特性动态调整排序策略，比如数据的分布情况或先前排序的历史记录。
- **数据预处理**：通过数据清洗和转换，改善排序前数据的质量，比如去除噪音或填充缺失值，这有助于提高排序算法的准确率。
- **并行化处理**：在支持并行计算的环境中，合理分解排序任务，充分利用多处理器或多线程，显著提高排序速度。

优化方法的选择和应用需要根据实际问题的具体情况来决定。例如，当处理的是结构化数据时，采用自适应排序策略可能更加有效。而对于大规模的非结构化数据，可能需要更多地依赖并行化处理来提高效率。

### 3.1.2 排序稳定性分析

排序算法的稳定性是一个重要的考量因素。排序稳定性指的是排序前后，具有相同键值的元素是否保持原来的相对顺序。稳定性对于某些应用场景至关重要，比如当需要对多个字段进行排序时，若保持稳定性，则可以保证在后续字段的排序中，前一个字段相同的元素保持相对位置不变。

为了实现稳定的排序，一种方法是在比较两个元素时，不仅仅基于要排序的键值，还考虑它们在原始数据中的位置。例如，在数组排序时，可以将元素的位置信息作为排序的次要键值，这样即使键值相同，位置信息的不同也可以帮助保持排序的稳定性。

## 3.2 多维数据结构的处理
### 3.2.1 多维数据模型

多维数据模型是支持复杂查询和分析的数据结构，常用于数据仓库和OLAP（在线分析处理）系统中。模型通常以多维数组或立方体的形式展现，每个维度代表一种数据特征，而数组的每个元素则代表了这些特征组合起来的数据项。

在处理这类数据时，直接应用传统排序算法可能不够高效，因为它们往往假定数据具有线性特性。因此，开发多维数据模型专用的排序算法变得尤为重要。例如，在多维空间中，排序算法不仅需要考虑数据点的值，还可能需要考虑它们的位置关系，如计算距离和角度等几何属性。

### 3.2.2 数据结构转换方法

为了使用传统的排序算法，我们需要将多维数