【稳定性与资源优化】：倒插法排序的稳定性质疑与内存使用策略

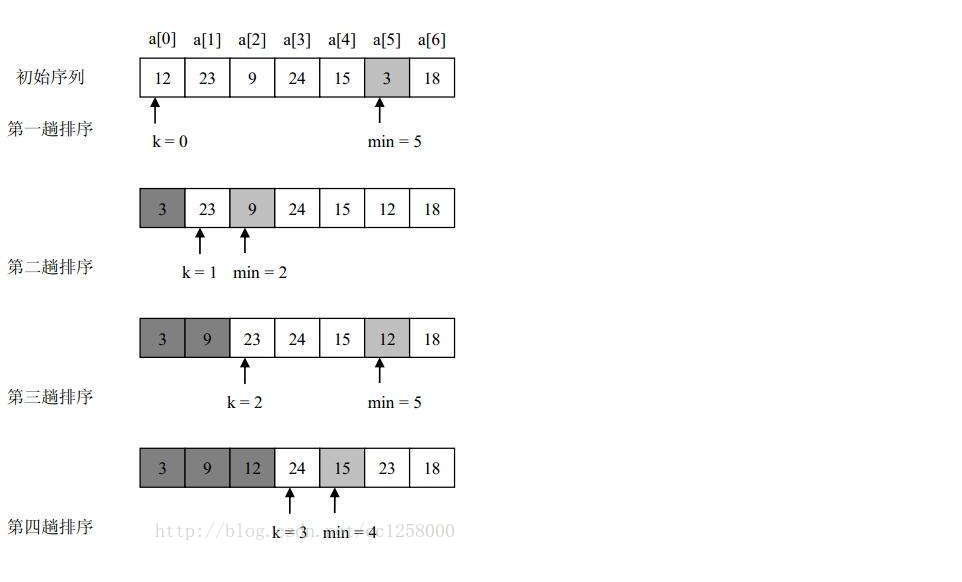
# 1. 倒插法排序算法简介

## 倒插法排序算法概述
倒插法排序（Insertion Sort）是一种简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。这种排序方法虽然在最坏情况下时间复杂度为O(n^2)，但因其简单和局部性好，在小规模数据或基本有序的数据集上表现优异。

## 倒插法排序的特点
该算法的特点是易于实现，无需额外的存储空间，是一种原地排序算法。虽然在大数据集上效率不是最优，但其在小数据集、数据基本有序或进行少量元素排序时效果显著。

## 倒插法排序的应用场景
倒插法排序最适合应用场景是数据量不大且数据基本有序时。例如，在一些特定的实时系统中，如网络请求处理或游戏帧循环中，需要对少量数据进行快速排序，倒插法排序是一个不错的选择。

接下来的文章中，我们会深入探讨倒插法排序算法的稳定性、内存使用效率，并与其他排序算法进行对比分析，以及它在实际应用中的表现和优化策略。

# 2. 倒插法排序的稳定性探讨

在这一章节中，我们将深入探讨倒插法排序算法的稳定性。排序算法的稳定性是衡量排序算法性能的一个重要指标，它不仅影响排序结果的正确性，还关系到算法的适用场景和效率。我们将首先定义稳定性在排序中的作用和它与数据结构的关系，随后深入分析倒插法排序的稳定性，并探讨稳定性对排序结果的影响，最后提供一些解决方案来改善排序算法的稳定性。

## 2.1 排序算法的稳定性定义

### 2.1.1 稳定性在排序中的作用

稳定性是排序算法的一个关键特性，它指的是当存在两个具有相同排序关键字的元素时，排序算法保证不会改变它们原始的相对位置。稳定性对于某些特定的数据处理场景非常重要，例如，在处理时间戳或者具有额外属性的记录时，如果两个记录具有相同的排序关键字（比如时间戳），我们通常希望保持它们原来的顺序，以便能够正确地处理数据。

### 2.1.2 稳定性与数据结构的关系

不同的数据结构对于排序算法的稳定性有不同的需求。例如，在链表中进行排序，由于链表的动态特性，实现一个稳定的排序算法比在数组中更容易。而数组由于其连续内存空间的特性，在不使用额外辅助空间的情况下，某些排序算法（比如快速排序）的稳定性就较难实现。

## 2.2 倒插法排序的稳定性分析

### 2.2.1 倒插法排序的实现原理

倒插法排序是一种简单的排序算法，其基本思想是从第一个元素开始，不断比较相邻的两个元素，如果它们的顺序错误就把它们交换过来。重复这个过程，直到最后一个元素，排序完成。这种排序方法简单直观，但它在交换过程中容易破坏相同元素的相对位置，导致算法的稳定性不足。

### 2.2.2 稳定性不足的原因探究

倒插法排序破坏稳定性的主要原因是其在排序过程中频繁进行元素交换。由于交换操作不考虑元素的相对大小，只是简单地比较和交换相邻元素，因此，如果两个元素的关键字相同，它们在排序过程中的相对位置可能会被改变。

### 2.2.3 稳定性与倒插法排序变体

倒插法排序的一个变体是改进的倒插法排序，它在交换时引入了额外的条件判断，确保在关键字相同的情况下不会发生交换。这虽然在一定程度上提高了排序的稳定性，但同时也牺牲了排序速度，因为引入了额外的判断逻辑。

## 2.3 稳定性对排序结果的影响

### 2.3.1 实例对比分析

为了更好地理解稳定性对排序结果的影响，我们可以构建一个例子。考虑一个数据集，其中包含多个元素对，每个元素对由一个标识符和一个日期组成。使用不稳定的倒插法排序和稳定的排序算法（如归并排序）对数据集进行排序，然后比较排序前后标识符的相对顺序。稳定的排序算法会保持日期相同的元素对的标识符相对顺序不变，而不稳定的排序算法则可能改变它们的相对顺序。

### 2.3.2 稳定性不足的解决方案

为了改善倒插法排序的稳定性，一个可能的解决方案是引入额外的数据结构或排序步骤。例如，可以在排序开始前记录下相同关键字元素对的相对位置，然后在排序完成后根据记录调整这些元素的位置。这种方法可以确保排序结果的正确性，但会增加算法的复杂性和运行时间。此外，也可以考虑使用稳定的排序算法，比如归并排序，作为倒插法排序的替代方案。

# 倒插法排序的Python实现示例
def insertion_sort(arr):
    for i in range(1, len(arr)):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:  # Change the direction of the comparison for stable sort
            arr[j + 1] = arr[j]
            j -= 1
        arr[j + 1] = key
    return arr

# 稳定性改进示例，通过记录元素位置
def stable_insertion_sort(arr, key_index):
    sorted_arr = []
    key_positions = {}
    for i in range(len(arr)):
        key_positions[arr[i][key_index]] = i
    for key in sorted(key_positions.keys()):
        sorted_arr.append(arr[key_positions[key]])
    return sorted_arr

# 示例数据
data = [(5, 'B'), (2, 'A'), (4, 'B'), (1, 'A'), (3, 'B')]
sorted_data = stable_insertion_sort(data, 1)  # Sort by second item in the tuple
print(sorted_data)

在以上代码中，我们首先展示了基本的倒插法排序算法，随后提供了一个改进版本，通过记录元素的位置来保持稳定性。这表明，在实际应用中，我们可以采取一些策略来保持倒插法排序的稳定性，但需要注意的是，这可能会增加算法的时间复杂度和空间复杂度。

# 3. 倒插法排序的内存使用效率

## 3.1 内存使用效率的衡量标准

### 3.1.1 时间复杂度与空间复杂度

排序算法的效率不仅体现在执行速度上，还体现在对内存资源的占用上。时间复杂度和空间复杂度是衡量一个算法效率的两个重要指标。时间复杂度描述了算法执行所需的时间量级，而空间复杂度则描述了算法执行过程中占用的额外空间量级。

在排序算法中，稳定的排序算法（如归并排序）往往具有较高的空间复杂度，因为它们需要额外的存储空间来保存数据的副本。倒插法排序（Insertion Sort）通常被认为是原地排序算法，因为它只需要一个额外的空间来暂存当前被比较的元素。

### 3.1.2 倒插法排序的空间需求分析

倒插法排序的空间复杂度为O(1)，这意味着除了输入数据本身所占用的空间外，它几乎不需要额外的内存空间。这是因为倒插法排序在进行元素比较和交换时，仅