ResNet18在图像分类中的应用：从理论到实践，助你掌握图像分类的完整流程

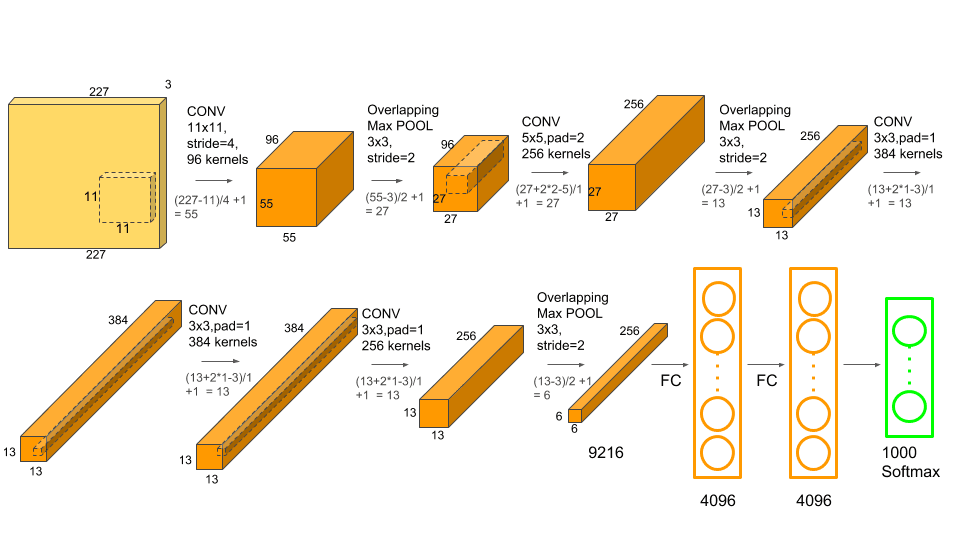
# 1. ResNet18网络结构与原理

ResNet18是一种深度残差网络，在图像分类任务中表现出色。其网络结构由一系列残差块组成，每个残差块包含两个卷积层和一个恒等映射。恒等映射允许梯度直接流过残差块，缓解了梯度消失问题，从而使网络能够训练得更深。

ResNet18的网络结构如下图所示：

graph LR
subgraph ResNet18
    A[Conv2d] --> B[ReLU] --> C[Conv2d] --> D[ReLU] --> E[Add] --> F[ReLU]
    E[Add] --> G[Conv2d] --> H[ReLU] --> I[Conv2d] --> J[ReLU] --> K[Add] --> L[ReLU]
    K[Add] --> M[Conv2d] --> N[ReLU] --> O[Conv2d] --> P[ReLU] --> Q[Add] --> R[ReLU]
    Q[Add] --> S[Conv2d] --> T[ReLU] --> U[Conv2d] --> V[ReLU] --> W[Add] --> X[ReLU]
    W[Add] --> Y[Conv2d] --> Z[ReLU] --> AA[Conv2d] --> BB[ReLU] --> CC[Add] --> DD[ReLU]
    CC[Add] --> EE[Conv2d] --> FF[ReLU] --> GG[Conv2d] --> HH[ReLU] --> II[Add] --> JJ[ReLU]
    II[Add] --> KK[Conv2d] --> LL[ReLU] --> MM[Conv2d] --> NN[ReLU] --> OO[Add] --> PP[ReLU]
    OO[Add] --> QQ[Conv2d] --> RR[ReLU] --> SS[Conv2d] --> TT[ReLU] --> UU[Add] --> VV[ReLU]
    VV[Add] --> WW[Conv2d] --> XX[ReLU] --> YY[Conv2d] --> ZZ[ReLU] --> AAA[Add] --> BBB[ReLU]
    BBB[Add] --> CCC[Conv2d] --> DDD[ReLU] --> EEE[Conv2d] --> FFF[ReLU] --> GGG[Add] --> HHH[ReLU]
    HHH[Add] --> III[Conv2d] --> JJJ[ReLU] --> KKK[Conv2d] --> LLL[ReLU] --> MMM[Add] --> NNN[ReLU]
    MMM[Add] --> OOO[Conv2d] --> PPP[ReLU] --> QQQ[Conv2d] --> RRR[ReLU] --> SSS[Add] --> TTT[ReLU]
    TTT[Add] --> UUU[Conv2d] --> VVV[ReLU] --> WWW[Conv2d] --> XXX[ReLU] --> YYY[Add] --> ZZZ[ReLU]
    ZZZ[Add] --> AAAA[Conv2d] --> BBBB[ReLU] --> CCCC[Conv2d] --> DDDD[ReLU] --> EEEE[Add] --> FFFF[ReLU]
    FFFF[Add] --> GGGG[Conv2d] --> HHHH[ReLU] --> IIII[Conv2d] --> JJJJ[ReLU] --> KKKK[Add] --> LLLL[ReLU]
    LLLL[Add] --> MMMM[Conv2d] --> NNNN[ReLU] --> OOOO[Conv2d] --> PPPP[ReLU] --> QQQQ[Add] --> RRRR[ReLU]
    RRRR[Add] --> SSSS[Conv2d] --> TTTT[ReLU] --> UUUU[Conv2d] --> VVVV[ReLU] --> WWWW[Add] --> XXXX[ReLU]
    XXXX[Add] --> YYYY[Conv2d] --> ZZZZ[ReLU] --> AAAAA[Conv2d] --> BBBBB[ReLU] --> CCCCC[Add] --> DDDDD[ReLU]
    DDDDD[Add] --> EEEEE[Conv2d] --> FFFFF[ReLU] --> GGGGG[Conv2d] --> HHHHH[ReLU] --> IIIII[Add] --> JJJJJ[ReLU]
    JJJJJ[Add] --> KKKKK[Conv2d] --> LLLLL[ReLU] --> MMMMM[Conv2d] --> NNNNN[ReLU] --> OOOOO[Add] --> PPPPP[ReLU]
    PPPPP[Add] --> QQQQQ[Conv2d] --> RRRRR[ReLU] --> SSSSS[Conv2d] --> TTTTT[ReLU] --> UUUUU[Add] --> VVVVV[ReLU]
    VVVVV[Add] --> WWWWW[Conv2d] --> XXXXX[ReLU] --> YYYYY[Conv2d] --> ZZZZZ[ReLU] --> AAAAAA[Add] --> BBBBBB[ReLU]
    BBBBB[Add] --> CCCCCC[Conv2d] --> DDDDDD[ReLU] --> EEEEEE[Conv2d] --> FFFFFF[ReLU] --> GGGGGG[Add] --> HHHHHH[ReLU]
    HHHHHH[Add] --> IIIIII[Conv2d] --> JJJJJJ[ReLU] --> KKKKKK[Conv2d] --> LLLLLL[ReLU] --> MMMMMM[Add] --> NNNNNN[ReLU]
    NNNNNN[Add] --> OOOOOO[Conv2d] --> PPPPPP[ReLU] --> QQQQQQ[Conv2d] --> RRRRRR[ReLU] --> SSSSSS[Add] --> TTTTTT[ReLU]
    TTTTTT[Add] --> UUUUUU[Conv2d] --> VVVVVV[ReLU] --> WWWWWW[Conv2d] --> XXXXXX[ReLU] --> YYYYYY[Add] --> ZZZZZZ[ReLU]
    ZZZZZZ[Add] --> AAAAAAA[Conv2d] --> BBBBBBB[ReLU] --> CCCCCCC[Conv2d] --> DDDDDDD[ReLU] --> EEEEEEEE[Add] --> FFFFFFF[ReLU]
    FFFFFFF[Add] --> GGGGGGG[Conv2d] --> HHHHHHHH[ReLU] --> IIIIIIII[Conv2d] --> JJJJJJJ[ReLU] --> KKKKKKK[Add] --> LLLLLLLL[ReLU]
    LLLLLLL[Add] --> MMMMMMMM[Conv2d] --> NNNNNNNN[ReLU] --> OOOOOOOO[Conv2d] --> PPPPPPPP[ReLU] --> QQQQQQQ[Add] --> RRRRRRRR[ReLU]
    RRRRRRR[Add] --> SSSSSSSS[Conv2d] --> TTTTTTTT[ReLU] --> UUUUUUUU[Conv2d] --> VVVVVVV[ReLU] --> WWWWWWWW[Add] --> XXXXXXXX[ReLU]
    XXXXXXXX[Add] --> YYYYYYYY[Conv2d] --> ZZZZZZZZ[ReLU] --> AAAAAAAA[Conv2d] --> BBBBBBBBB[ReLU] --> CCCCCCCCC[Add] --> DDDDDDDDD[ReLU]
    DDDDDDDD[Add] --> EEEEEEEEE[Conv2d] --> FFFFFFFF[ReLU] --> GGGGGGGG[Conv2d] --> HHHHHHHHH[ReLU] --> IIIIIIIII[Add] --> JJJJJJJJ[ReLU]
    JJJJJJJ[Add] --> KKKKKKKK[Conv2d] --> LLLLLLLL[ReLU] --> MMMMMMMMM[Conv2d] --> NNNNNNNNN[ReLU] --> OOOOOOOOO[Add] --> PPPPPPPPP[ReLU]
    PPPPPPPP[Add] --> QQQQQQQQ[Conv2d] --> RRRRRRRR[ReLU] --> SSSSSSSS[Conv2d] --> TTTTTTTT[ReLU] --> UUUUUUUUU[Add] --> VVVVVVV