GMM的Python实现指南：用代码探索模型的实际应用，快速上手

# 1. GMM模型理论基础**

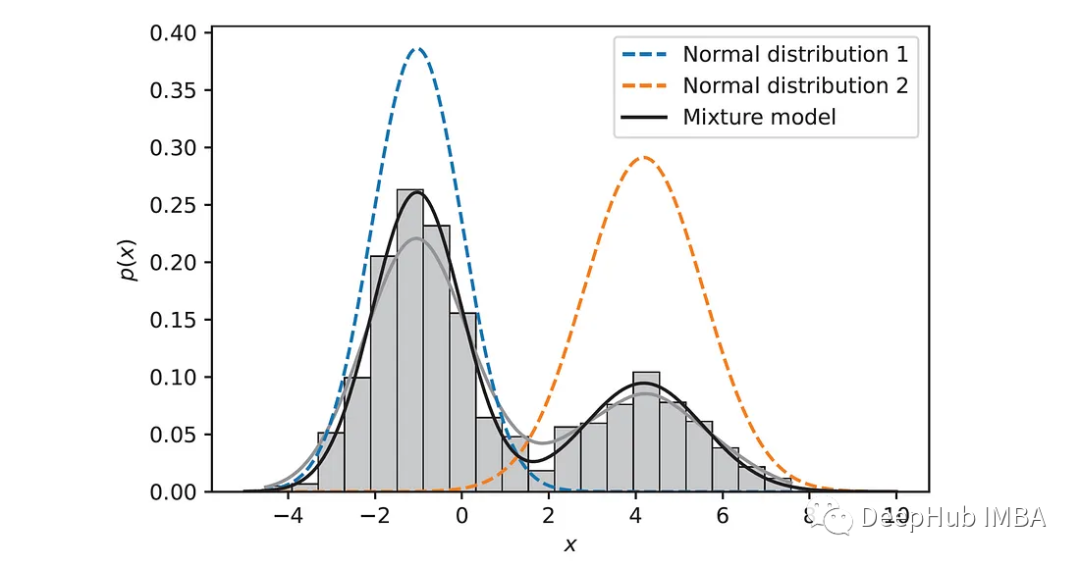
高斯混合模型（GMM）是一种概率生成模型，它假设数据是由多个高斯分布的混合产生的。每个高斯分布代表一个簇，簇的权重表示该簇在数据中的比例。

GMM模型的参数包括：
- 高斯分布的均值和协方差矩阵
- 每个簇的权重

GMM模型的训练过程使用期望最大化（EM）算法，它通过迭代地估计模型参数和分配数据点到簇来最大化数据的似然函数。

# 2. Python实现GMM模型

### 2.1 GMM模型在Python中的库和函数

#### 2.1.1 scikit-learn库中的GMM类

scikit-learn库提供了`GaussianMixture`类，用于实现GMM模型。该类提供了以下主要方法：

- `__init__`: 初始化GMM模型，指定高斯混合组件的数量、协方差类型等参数。
- `fit`: 拟合模型，估计模型参数。
- `predict`: 根据模型对新数据进行预测，返回每个样本属于每个组件的概率。
- `score`: 计算模型的得分，衡量模型的拟合优度。

#### 2.1.2 GMM模型的初始化和训练

import numpy as np
from sklearn.mixture import GaussianMixture

# 初始化GMM模型，指定3个高斯混合组件
gmm = GaussianMixture(n_components=3)

# 训练模型，拟合数据
gmm.fit(data)

### 2.2 GMM模型的参数估计

#### 2.2.1 EM算法的原理和实现

EM算法是一种用于估计GMM模型参数的迭代算法。其过程如下：

1. **E步（期望步骤）：**计算每个样本属于每个组件的期望概率。
2. **M步（最大化步骤）：**根据期望概率，更新模型参数（均值、协方差、混合系数）。
3. 重复E步和M步，直到模型收敛。

scikit-learn库中使用Baum-Welch算法实现了EM算法，该算法通过最大化模型的对数似然函数来更新参数。

#### 2.2.2 GMM模型的拟合和参数估计

# 拟合GMM模型
gmm.fit(data)

# 获取模型参数
means = gmm.means_  # 均值
covariances = gmm.covariances_  # 协方差
weights = gmm.weights_  # 混合系数

### 2.3 GMM模型的评估和选择

#### 2.3.1 模型评估指标

常用的GMM模型评估指标包括：

- **对数似然函数：**衡量模型拟合数据的优度。
- **赤池信息准则（AIC）：**考虑模型复杂度和拟合优度的综合指标。
- **贝叶斯信息准则（BIC）：**类似于AIC，但对模型复杂度的惩罚更大。