链表的排序算法及实现细节

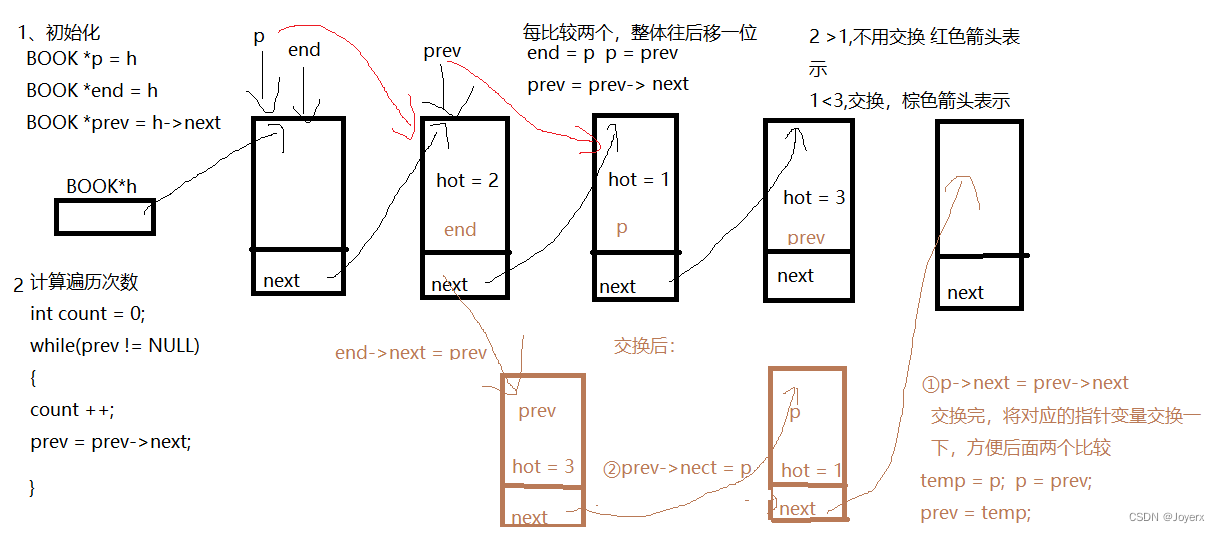
# 1. 链表排序算法理论基础

链表排序算法是针对链表数据结构设计的排序算法，与数组排序算法不同，链表排序算法需要考虑链表的特殊性，如节点之间的指针关系。

### 2.1 比较类排序算法

比较类排序算法通过逐个比较元素，将较小的元素移动到前面，较大的元素移动到后面，从而达到排序的目的。

#### 2.1.1 冒泡排序

冒泡排序通过逐个比较相邻元素，将较小的元素交换到前面，较大的元素交换到后面，反复进行直到所有元素排序完成。其时间复杂度为 O(n^2)，空间复杂度为 O(1)。

# 2. 链表排序算法理论基础

### 2.1 比较类排序算法

比较类排序算法是通过比较相邻元素的大小来进行排序。比较类排序算法的思想是：将待排序的序列看成一个无序的集合，然后通过不断地比较相邻元素的大小，将较小的元素移动到前面，较大的元素移动到后面，直到整个序列有序。

#### 2.1.1 冒泡排序

冒泡排序是一种简单的比较类排序算法。冒泡排序的思想是：将待排序的序列看成一个无序的集合，然后通过不断地比较相邻元素的大小，将较小的元素移动到前面，较大的元素移动到后面，直到整个序列有序。

**算法流程：**

1. 从第一个元素开始，与后面的元素逐个比较，如果当前元素大于后面的元素，则交换这两个元素的位置。
2. 重复步骤 1，直到最后一个元素。
3. 将最后一个元素与前面的元素逐个比较，如果当前元素小于前面的元素，则交换这两个元素的位置。
4. 重复步骤 3，直到第一个元素。

**代码实现：**

def bubble_sort(arr):
    """冒泡排序算法

    Args:
        arr: 待排序的数组

    Returns:
        排序后的数组
    """

    n = len(arr)
    for i in range(n):
        for j in range(0, n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]

    return arr

**逻辑分析：**

* 外层循环 `for i in range(n)` 控制冒泡排序的趟数。
* 内层循环 `for j in range(0, n - i - 1)` 控制每趟比较的次数。
* `if arr[j] > arr[j + 1]` 判断相邻元素是否需要交换。
* `arr[j], arr[j + 1] = arr[j + 1], arr[j]` 交换相邻元素。

#### 2.1.2 选择排序

选择排序也是一种简单的比较类排序算法。选择排序的思想是：将待排序的序列看成一个无序的集合，然后通过不断地找出最小的元素，并将其移动到前面，直到整个序列有序。

**算法流程：**

1. 从第一个元素开始，找出剩余元素中的最小值。
2. 将最小值与第一个元素交换位置。
3. 重复步骤 1 和 2，直到最后一个元素。

**代码实现：**

def selection_sort(arr):
    """选择排序算法

    Args:
        arr: 待排序的数组

    Returns:
        排序后的数组
    """

    n = len(arr)
    for i in range(n):
        min_idx = i
        for j in range(i + 1, n):
            if arr[j] < arr[min_idx]:
                min_idx = j

        arr[i], arr[min_idx] = arr[min_idx], arr[i]

    return arr

**逻辑分析：**

* 外层循环 `for i in range(n)` 控制选择排序的趟数。
* 内层循环 `for j in range(i + 1, n)` 控制每趟比较的次数。
* `if arr[j] < arr[min_idx]` 判断当前元素是否比最小值小。
* `arr[i], arr[min_idx] = arr[min_idx], arr[i]` 交换最小值与当前元素。

#### 2.1.3 插入排序

插入排序也是一种简单的比较类排序算法。插入排序的思想是：将待排序的序列看成一个无序的集合，然后通过不断地将一个元素插入到前面已排序的序列中，直到整个序列有序。

**算法流程：**

1. 从第二个元素开始，与前面的元素逐个比较，如果当前元素小于前面的元素，则将当前元素插入到前面的元素之前。
2. 重复步骤 1，直到最后一个元素。

**代码实现：**

def insertion_sort(arr):
    """插入排序算法

    Args:
        arr: 待排序的数组

    Returns:
        排序后的数组
    """

    n = len(arr)
    for i in range(1, n):
        key = arr[i]
        j = i - 1
        while j >= 0 and key < arr[j]:
            arr[j + 1] = arr[j]
            j -= 1

        arr[j + 1] = key

    return arr

**逻辑分析