使用递归思想解决链表问题的指导原则

# 1. 链表的基本概念和操作**

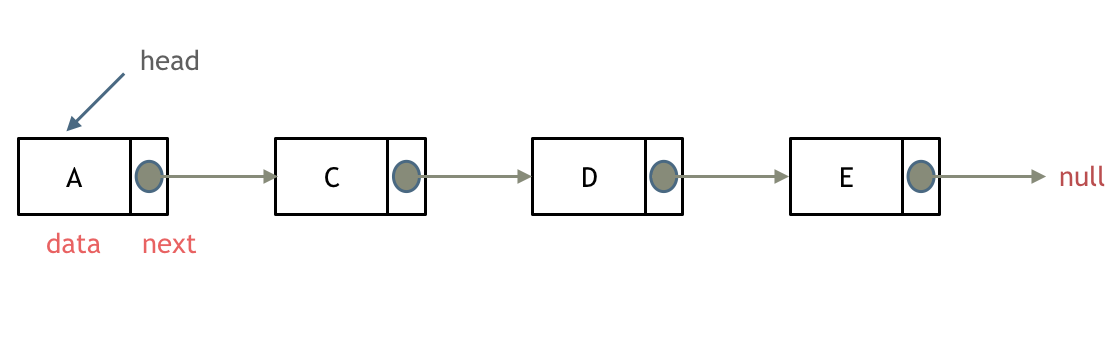
链表是一种线性数据结构，由一系列节点组成，每个节点包含一个数据元素和指向下一个节点的指针。链表具有以下特点：

- **动态分配内存：**链表的节点在运行时动态分配，不需要预先分配固定大小的内存空间。
- **插入和删除高效：**可以在链表的任意位置高效地插入或删除节点，而无需移动其他节点。
- **顺序访问困难：**由于链表节点之间是通过指针连接的，因此无法直接访问指定位置的节点，需要从头遍历整个链表。

# 2. 递归在链表中的应用

### 2.1 递归的原理和特点

递归是一种计算机科学中常用的编程技巧，它允许函数调用自身来解决问题。递归函数通常包含两个部分：基线条件和递归步骤。

* **基线条件：**这是递归函数停止调用的条件，它通常是问题的简单或特殊情况。
* **递归步骤：**这是递归函数调用自身的步骤，它将问题分解成更小的子问题，并使用递归函数来解决这些子问题。

递归具有以下特点：

* **简洁性：**递归代码通常比迭代代码更简洁，因为它可以利用函数自身来解决问题。
* **可扩展性：**递归代码很容易扩展到更复杂的问题，因为它可以分解问题并逐层解决。
* **效率：**递归代码在某些情况下可能效率不高，因为函数调用会产生开销。

### 2.2 链表的递归遍历

递归可以用来遍历链表，正序或逆序。

#### 2.2.1 递归正序遍历

def traverse_forward(node):
    """
    递归正序遍历链表

    参数：
        node: 当前链表节点

    返回：
        None
    """
    if node is None:
        return

    # 访问当前节点
    print(node.data)

    # 递归遍历下一个节点
    traverse_forward(node.next)

**代码逻辑：**

* 如果当前节点为 `None`，则停止遍历。
* 访问当前节点的数据。
* 递归调用 `traverse_forward` 函数，传入当前节点的 `next` 节点。

#### 2.2.2 递归逆序遍历

def traverse_backward(node):
    """
    递归逆序遍历链表

    参数：
        node: 当前链表节点

    返回：
        None
    """
    if node is None:
        return

    # 递归遍历下一个节点
    traverse_backward(node.next)

    # 访问当前节点
    print(node.data)

**代码逻辑：**

* 如果当前节点为 `None`，则停止遍历。
* 递归调用 `traverse_backward` 函数，传入当前节点的 `next` 节点。
* 访问当前节点的数据。

### 2.3 链表的递归查找

递归也可以用来在链表中查找元素。

#### 2.3.1 递归查找指定元素

def find_element(node, target):
    """
    递归查找链表中指定元素

    参数：
        node: 当前链表节点
        target: 要查找的元素

    返回：
        如果找到元素，返回 True；否则返回 False
    """
    if node is None:
        return False

    # 检查当前节点是否为目标元素
    if node.data == target:
        return True

    # 递归查找下一个节点
    return find_element(node.next, target)

**代码逻辑：**

* 如果当前节点为 `None`，则停止查找。
* 检查当前节点的数据是否等于目标元素。
* 如果是，则返回 `True`。
* 否则，递归调用 `find_element` 函数，传入当前节点的 `next` 节点和目标元素。

#### 2.3.2 递归查找元素位置

def find_position(node, target):
    """
    递归查找链表中元素的位置

    参数：
        node: 当前链表节点
        target: 要查找的元素

    返回：
        如果找到元素，返回元素的位置；否则返回 -1
    """
    if node is None:
        return -1

    # 检查当前节点是否为目标元素
    if node.data == target:
        return 0

    # 递归查找下一个节点
    position = find_position(node.next, target)

    # 如果找到元素，则返回位置 + 1
    if position != -1:
        return position + 1

    # 否则，返回 -1
    return -1

**代码逻辑：**

* 如果当前节点为 `None`，则停止查找。
* 检查当前节点的数据是否等于目标元素。
* 如果是，则返回 `0`。
* 否则，递归调用 `find_position` 函数，传入当前节点的 `next` 节点和目标元素。
* 如果找到元素，则返回位置 + 1。
* 否则，返回 -1。

# 3. 递归解决链表问题的实践

### 3.1 递归反转链表

**问题描述：**
给定一个链表，反转其顺序。

**递归解法：**
反转链表的递归解法遵循“分治”思想，将链表划分为两部分：头结点和剩余部分。

1. **递归基线：**当链表为空或只有一个元素时，直接返回。
2. **分解问题：**将链表的头结点 `head` 作为新的尾结点，然后递归反转剩余部分 `rest`。
3. **合并结果：**将反转后的剩余部分 `rest` 的尾结点指向 `head`，并将 `head` 的 `next` 指针指向 `null`。

**代码实现：**

def reverse_list(head):
    """
    反转链表。

    参数：
        head: 链表的头结点。

    返回：
        反转后的链表的头结点。
    """
    # 递归基线
    if head is None or head.next is None:
        return head

    # 分解问题
    rest = reverse_list(head.next)

    # 合并结果
    head.next.next = head
    head.next = None

    return rest

**逻辑分析：**

* `reverse_list` 函数接收链表的头结点 `head` 作为参数，返回反转后的链表的头结点。
* 如果链表为空或只有一个元素，则直接返回 `head`。
* 否则，递归调用 `reverse_list` 函数反转剩余部分 `rest`。
* 将反转后的剩余部分 `rest` 的尾结点指向 `head`，并将 `head` 的 `next` 指针指向 `null