掌握链表的核心原理，开启数据结构之旅

# 1. 链表的基本概念和结构**

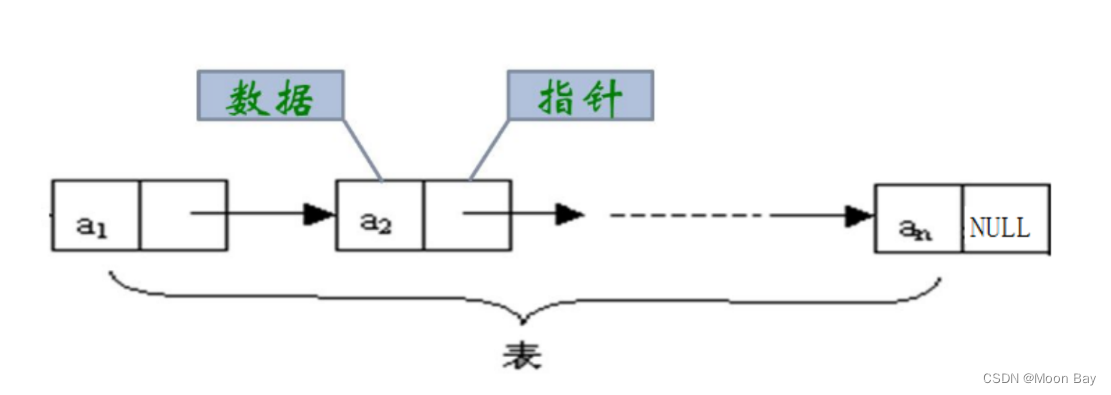
链表是一种线性数据结构，由一系列节点组成，每个节点包含数据和指向下一个节点的指针。与数组不同，链表中的节点可以在内存中分散存储，从而提供了插入和删除元素的灵活性。

链表的基本结构如下：

graph LR
A[Node 1] --> B[Node 2] --> C[Node 3]

每个节点包含一个数据字段（例如 `data`) 和一个指向下一个节点的指针（例如 `next`)。头节点指向链表的第一个节点，尾节点指向链表的最后一个节点。

# 2.1 链表的存储结构和特性

### 链表的存储结构

链表是一种线性数据结构，其元素之间通过指针连接。每个元素（称为节点）包含两个部分：数据域和指针域。数据域存储实际数据，而指针域存储指向下一个节点的指针。

struct Node {
    int data;
    Node* next;
};

### 链表的特性

* **非连续存储：**链表中的节点存储在内存的不同位置，因此不是连续的。
* **动态分配：**链表中的节点在需要时动态分配，不需要时释放。
* **插入和删除方便：**在链表中插入或删除节点不需要移动其他节点，只需更新指针即可。
* **顺序访问困难：**由于链表中的节点不是连续存储的，因此顺序访问链表中的元素需要遍历整个链表。

### 链表与数组的比较

| 特性 | 链表 | 数组 |
|---|---|---|
| 存储结构 | 非连续 | 连续 |
| 内存分配 | 动态分配 | 静态分配 |
| 插入和删除 | 方便 | 困难 |
| 顺序访问 | 困难 | 方便 |

## 2.2 链表的节点操作

### 2.2.1 节点的插入和删除

**插入节点：**

* 在链表的开头插入节点：将新节点的指针指向链表头，然后将链表头更新为新节点。
* 在链表的中间插入节点：找到要插入节点之前的位置，然后将新节点的指针指向该位置的下一个节点，并将该位置的下一个节点更新为新节点。
* 在链表的末尾插入节点：找到链表的尾节点，然后将新节点的指针指向尾节点，并将尾节点更新为新节点。

**删除节点：**

* 删除链表的第一个节点：将链表头更新为链表头的下一个节点。
* 删除链表的中间节点：找到要删除节点的前一个节点，然后将前一个节点的指针指向要删除节点的下一个节点。
* 删除链表的最后一个节点：找到链表的尾节点的前一个节点，然后将尾节点的前一个节点的指针指向空。

### 2.2.2 节点的查找和遍历

**查找节点：**

从链表头开始，逐个比较节点的数据域，直到找到要查找的节点。

Node* findNode(Node* head, int data) {
    while (head != NULL) {
        if (head->data == data) {
            return head;
        }
        head = head->next;
    }
    return NULL;
}

**遍历链表：**

从链表头开始，逐个访问节点，直到链表尾。

void traverseList(Node* head) {
    while (head != NULL) {
        printf("%d ", head->data);
        head = head->next;
    }
}

# 3. 链表的实践应用

### 3.1 单链表的实现

#### 3.1.1 单链表的节点结构

单链表的节点通常包含两个部分：数据域和指针域。数据域存储实际数据，而指针域指向下一个节点。

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None

#### 3.1.2 单链表的基本操作

单链表的基本操作包括：

- **插入节点：**在指定位置插入一个新节点。
- **删除节点：**删除指定位置的节点。
- **查找节点：**根据数据值查找节点。
- **遍历链表：**从头到尾遍历链表中的所有节点。

### 3.2 双链表的实现

#### 3.2.1 双链表的节点结构

双链表的节点与单链表类似，但它有两个指针域：一个指向下一个节点，另一个指向前一个节点。

class Node:
    def __init__(self, data):
        self.data = data
        self.next = None
        self.prev = None

#### 3.2.2 双链表的基本操作

双链表的基本操作与单链表类似，但它还包括一些额外的操作，例如：

- **插入节点：**在指定位置插入一个新节点。
- **删除节点：**删除指定位置的节点。
- **查找节点：**根据数据值查找节点。
- **遍历链表：**从头到尾或从尾到头遍历链表中的所有节点。

### 代码示例

以下代码示例演示了单链表和双链表的基本操作：

# 单链表示例
head = Node(1)
head.next = Node(2)
head.next.next = Node(3)

# 插入节点
new_node = Node(4)
new_node.next = head.next
head.next = new_node

# 删除节点
head.next = head.next.next

# 遍历链表
current_node = head
while current_node is not None:
    print(current_node.data)
    current_node = current_node.next

# 双链表示例
head = No