【Java加密算法选择宝典】：如何智慧选择加密算法

# 1. 加密算法概述与应用领域

加密技术是信息安全领域的基石，随着互联网和数字时代的飞速发展，其应用领域不断拓宽，从最初的军事通讯到如今的电子商务、网络安全和个人隐私保护。加密算法，简单来说，是一系列复杂的数学运算，这些运算用于转化原始数据，使其在未授权的情况下不可读，从而保障数据的安全性和完整性。通过对数据进行加密和解密，可以有效地防止敏感信息被非法窃取和篡改。

加密算法在技术层面可以大致分为对称加密和非对称加密两大类。对称加密使用相同的密钥进行数据的加密和解密，其优点在于速度快，效率高，非常适合大量数据的处理；而非对称加密使用一对不同的密钥，即公钥和私钥，这样既确保了加密的安全性，又方便了密钥的分发和管理。除此之外，哈希函数和消息摘要算法也是信息安全不可或缺的部分，它们主要用于数据完整性校验和数字签名的生成。

在本章中，我们将对加密算法的基本概念、应用领域以及它们在现代信息技术中的作用进行简要介绍，为后续章节深入探讨各种加密技术打下基础。

# 2. 对称加密算法的原理与实践

## 2.1 对称加密算法的基本概念

### 2.1.1 对称加密的工作原理
对称加密算法的核心在于加密与解密过程使用相同的密钥。这个密钥必须在通信双方之间安全地共享。在加密过程中，数据通过某种方式与密钥结合，生成密文，这使得只有持有相同密钥的人才能将密文还原为原始数据（解密）。对称加密算法包括分组加密和序列加密两大类，其中分组加密算法将数据分组处理，而序列加密算法则一次处理一个比特。

### 2.1.2 常见的对称加密算法简介
常见的对称加密算法包括AES、DES、3DES、Blowfish等。高级加密标准（AES）是目前广泛使用的对称加密算法，而数据加密标准（DES）已经由于密钥长度短而变得不再安全。3DES是对DES算法的一种改进，通过对数据多次加密来增强安全性。Blowfish则是一种分组密码，其设计结构简单，加解密速度快。

## 2.2 对称加密算法的实现与比较

### 2.2.1 AES算法的实现细节
AES算法支持128、192、和256位三种不同的密钥长度。其加密过程基于替代-置换网络原理，包括字节替代、行移位、列混合和轮密钥加四个阶段。在实际实现时，开发者通常会使用一些成熟的加密库如OpenSSL、Crypto++或Java的加密API来简化开发流程。

#include <openssl/aes.h>

// AES加密示例代码
void aes_encrypt(const unsigned char *plaintext, const AES_KEY *key, unsigned char *ciphertext) {
    AES_encrypt(plaintext, ciphertext, key);
}

// AES解密示例代码
void aes_decrypt(const unsigned char *ciphertext, const AES_KEY *key, unsigned char *plaintext) {
    AES_decrypt(ciphertext, plaintext, key);
}

在上述代码块中，使用了OpenSSL库的AES加密和解密方法。开发者需要先初始化一个AES_KEY结构体，这涉及到密钥的设置。

### 2.2.2 DES与3DES算法的优劣分析
DES算法因为其56位的密钥长度，现在容易受到暴力破解的攻击，因此在许多国家和地区已经不被推荐使用。3DES是对DES的一个强化版本，它通过三个56位密钥来提供更高级别的安全性。尽管如此，由于3DES在加解密过程中需要更多的计算资源，因此它的速度比AES要慢。

| 对比项 | DES | 3DES | AES |
|----------|------------------|------------------|-----------------|
| 密钥长度 | 56位 | 112或168位 | 128、192、256位 |
| 加密速度 | 较快 | 较慢 | 快 |
| 安全性 | 较低 | 较高 | 很高 |

### 2.2.3 其他对称加密算法的简介与适用场景
除了前面提到的几种算法外，还有许多对称加密算法，如Blowfish、Twofish、Camellia等。Blowfish以其算法简单、速度快的特点而被广泛使用。Twofish是Blowfish的后继算法，它在安全性上做了进一步提升。Camellia是一种高效的对称加密算法，特别适合资源受限的环境，如智能卡和移动设备。

## 2.3 对称加密算法的性能评估与选择

### 2.3.1 安全性考量
安全性是选择对称加密算法时的首要因素。应当考虑到算法的密钥长度、是否存在已知的安全漏洞以及抵抗攻击的能力。除了这些技术因素外，还要考虑到使用的行业标准和法规要求。

### 2.3.2 性能考量：速度与资源消耗
性能评估需要在实际使用场景下进行。加密和解密的速度直接关系到系统的响应时间和吞吐量，特别是在需要实时加密大量数据的应用中。资源消耗则涉及到对系统内存和CPU的占用情况。在资源有限的环境中，算法的效率和灵活性显得尤为重要。

### 2.3.3 选择对称加密算法的实际建议
根据不同的使用场景，选择合适的对称加密算法需要综合考量安全性、性能和合规性。例如，对于需要高安全性和可扩展性的金融行业，AES-256可能是更好的选择。对于资源受限的物联网设备，可能需要优先考虑Camellia或其他轻量级加密算法。

在实践中，对称加密算法的选择还需要考虑到算法实现的成熟度、第三方库的支持、以及社区反馈等因素。通过综合评估和测试，开发者可以选出最适合特定应用需求的加密算法。

总结上述内容，对称加密算法在保证数据安全的前提下，其性能和资源占用情况同样关键。正确的选择和实现对称加密算法，能够在保障数据机密性的同时，满足应用对速度和资源的严格要求。

# 3. 非对称加密算法的原理与实践

## 3.1 非对称加密算法的基本概念

### 3.1.1 非对称加密的工作原理

非对称加密算法（Asymmetric Encryption Algorithms）是基于一对数学相关的密钥：公钥（Public Key）和私钥（Private Key）。这种加密方式的主要特点是加密密钥和解密密钥可以不同，而且从公钥几乎不可能推算出私钥。非对称加密的一个重要用途是数字签名，它可以验证消息的完整性和来源。

与对称加密相比，非对称加密的一个关键优势是密钥分发问题。由于非对称加密可以公开分发公钥，从而消除了密钥交换的问题。不过，非对称加密的计算成本相对较高，因此在速度上通常慢于对称加密，因此两者往往结合使用，以兼顾安全性和效率。

### 3.1.2 常见的非对称加密算法简介

最著名的非对称加密算法之一是RSA，由Rivest, Shamir, 和Adleman在1977年提出，其安全性基于大整数分解的难度。RSA加密算法支持加密和数字签名。

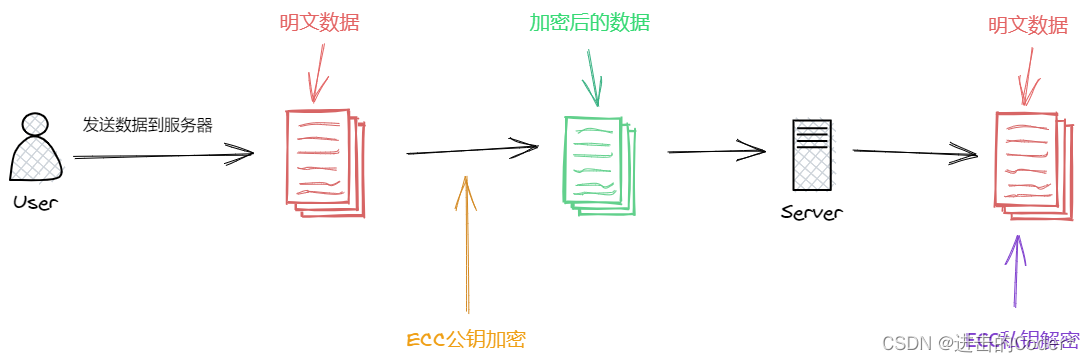
除了RSA之外，椭圆曲线加密（Elliptic Curve Cryptography, ECC）是另一个越来越受欢迎的非对称加密算法。ECC依赖于椭圆曲线数学，能够在更小的密钥长度上提供与RSA相当甚至更高的安全性，因此在移动设备和硬件受限的应用场景中非常受欢迎。

另一个例子是Diffie-Hellman密钥交换（DH），该协议允许双方在没有共享密钥的情况下建立一个共享的秘密。尽管它不是一个完整的加密算法，但它是非对称加密技术中的重要组成部分。

## 3.2 RSA算法的实现与特点

### 3.2.1 RSA算法的基本原理

RSA算法是一种公钥加密技术，它利用了大数分解的难题，即根据已知的公钥（n,e），找到私钥（n,d）是计算上不可行的。这里的n是两个大素数的乘积，而e和d是基于欧拉函数φ(n)的指数关系。加密过程就是将明文P与公钥(n,e)进行运算得到密文C，解密则是将密文C与私钥(n,d)进行运算得到明文P。

### 3.2.2 密钥的生成与管理

在RSA算法中，密钥的生成是一个关键步骤。一个典型的RSA密钥生成过程包括以下步骤：

1. 选择两个大的质数p和q。
2. 计算它们的乘积n = p*q，n的长度就是密钥长度。
3. 计算n的欧拉函数φ(n) = (p-1)*(q-1)。
4. 选择一个整数e，使得1 < e < φ(n)，且e和φ(n)互质。
5. 计算e关于φ(n)的模逆元d，使得e*d mod φ(n) = 1。
6. 公钥是(n,e)，私钥是(n,d)。

密钥的管理涉及到密钥的安全存储、定期更新以及密钥的有效期管理。在实际应用中，私钥尤其需要保护，因为它直接关系到加密系统的安全性。

### 3.2.3 RSA算法的性能特点

RSA算法在加密和解密过程中需要进行大数的模幂运算，这导致了它在计算上相当耗时，特别是在密钥长度较大时。因此，RSA算法通常用于加密较短的数据，比如一个对称加密的密钥，而对称加密算法则用于加密大部分数据。

此外，由于RSA算法的安全性依赖于大数的质因数分解难度，密钥长度的选择至关重要。随着计算能力的提高，更长的密钥（如2048位或更长）被推荐用于保持足够的安全性。

### 3.2.4 RSA算法的代码实现与分析

import java.security.KeyPair;
import java.security.KeyPairGenerator;
import java.security.PrivateKey;
import java.security.PublicKey;

public class RSAExample {
    public static void main(String[] args) throws Exception {
        // 生成RSA密钥对
        KeyPairGenerator keyPairGenerator = KeyPairGenerator.getInstance("RSA");
        keyPairGenerator.initialize(2048); // 初始化密钥长度
        KeyPair keyPair = keyPairGenerator.generateKeyPair();

        // 获取公钥和私钥
        PublicKey publicKey = keyPair.getPublic();
        PrivateKey privateKey = keyPair.getPrivate();

        // 这里可以添加代码用于加密和解密数据，例如：
        // String message = "Hello, RSA!";
        // byte[] encryptedData = rsaEncrypt(message.getBytes(), publicKey);
        // byte[] decryptedData = rsaDecrypt(encryptedData, privateKey);
        // 输出生成的密钥信息
        System.out.println("Public Key: " + publicKey);
        System.out.println("Private Key: " + privateKey);
    }
}

在上述Java代码中，我们生成了一个2048位的RSA密钥对。代码中使用了`KeyPairGenerator`类来创建密钥对，设置密钥长度为2048位，这在当前是安全实践推荐的密钥长度。通过调用`generateKeyPair`方法，我们获得了`PublicKey`和`PrivateKey`对象，分别用于加密和解密。

在实际应用中，`rsaEncrypt`和`rsaDecrypt`方法将使用RSA算法进行加密和解密操作。这些方法涉及到大数运算，通常使用Java加密扩展（JCE）提供的算法实现。

## 3.3 ECC与其它非对称加密算法

### 3.3.1 ECC算法的原理与优势

ECC（Elliptic Curve Cryptography）算法基于椭圆曲线数学，在密钥长度远小于RSA的情况下，可以提供相同甚至更高的安全级别。ECC算法的安全性依赖于椭圆曲线离散对数问题的困难性。

ECC的一个关