栈在图论中的算法应用

# 2.1 深度优先搜索（DFS）

### 2.1.1 DFS算法原理和实现

深度优先搜索（DFS）是一种图论算法，它通过递归或栈来遍历图中的节点。DFS从一个起始节点开始，并沿着一条路径深度遍历，直到无法再继续遍历为止。然后，DFS回溯到最近未访问的节点，并继续沿着另一条路径遍历。

DFS的实现通常使用栈数据结构。栈是一种后进先出（LIFO）数据结构，它存储要访问的节点。DFS算法将起始节点压入栈中，然后循环执行以下步骤：

1. 从栈中弹出顶部节点。
2. 访问该节点。
3. 将该节点的所有未访问的邻接节点压入栈中。
4. 重复步骤1-3，直到栈为空。

### 2.1.2 DFS在图论中的应用

DFS在图论中有着广泛的应用，包括：

* 检测图中的环
* 查找图中的连通分量
* 求解迷宫问题
* 拓扑排序

# 2. 栈在图论中的基本应用

### 2.1 深度优先搜索（DFS）

#### 2.1.1 DFS算法原理和实现

深度优先搜索（DFS）是一种图论算法，用于遍历图中的所有节点。其基本原理是：从起始节点出发，沿着一条路径一直向下遍历，直到无法再继续遍历为止，然后再回溯到上一个未遍历的节点，继续向下遍历。

DFS算法的实现通常使用栈数据结构。具体步骤如下：

1. 将起始节点压入栈中。
2. 只要栈不为空，就弹出栈顶节点并访问它。
3. 如果当前节点有未访问的邻接节点，则将邻接节点压入栈中。
4. 重复步骤2和3，直到栈为空。

#### 2.1.2 DFS在图论中的应用

DFS算法在图论中有着广泛的应用，包括：

* **连通性检测：**确定图中哪些节点是连通的。
* **环检测：**判断图中是否存在环。
* **拓扑排序：**对无环图中的节点进行排序，使得每个节点都位于其所有后继节点之前。
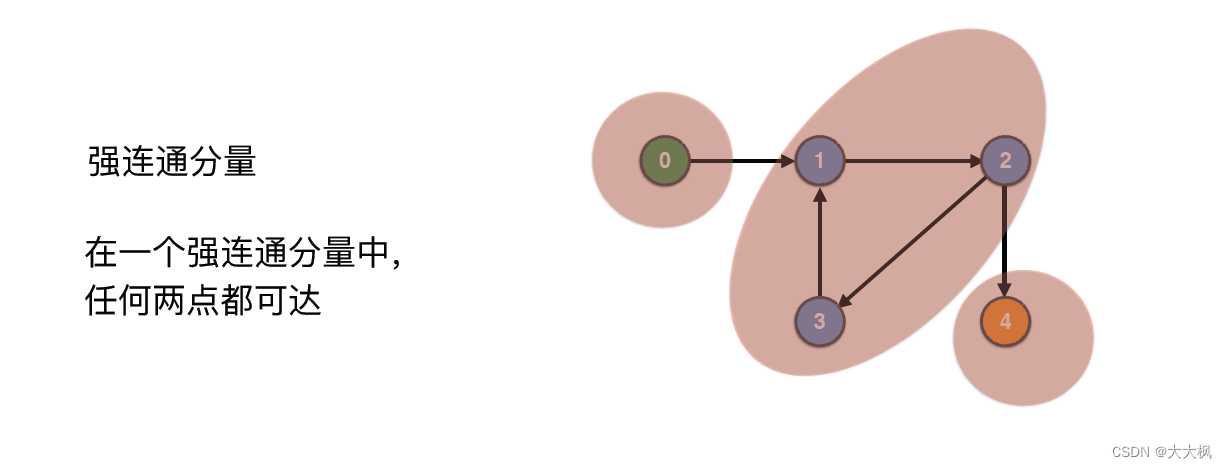
* **强连通分量：**找出图中所有强连通分量，即不能被任何割边或割点分开的节点集合。

### 2.2 广度优先搜索（BFS）

#### 2.2.1 BFS算法原理和实现

广度优先搜索（BFS）也是一种图论算法，用于遍历图中的所有节点。其基本原理是：从起始节点出发，先遍历其所有邻接节点，然后再遍历邻接节点的邻接节点，以此类推，直到遍历完所有节点。

BFS算法的实现通常使用队列数据结构。具体步骤如下：

1. 将起始节点入队。
2. 只要队列不为空，就出队队首节点并访问它。
3. 如果当前节点有未访问的邻接节点，则将邻接节点入队。
4. 重复步骤2和3，直到队列为空。

#### 2.2.2 BFS在图论中的应用

BFS算法在图论中也有着广泛的应用，包括：

* **最短路径：**找出图中从起始节点到其他节点的最短路径。
* **最大流：**计算图中从源节点到汇节点的最大流。
* **最小割：**找出图中将源节点与汇节点分开的最小割。
* **二分图匹配：**判断图是否是二分图，并找出二分图中的最大匹配。

### 2.2.3 DFS和BFS的比较

DFS和BFS是图论中两种重要的算法，各有其优缺点：

| 特征 | DFS | BFS |
|---|---|---|
| 遍历顺序 | 深度优先 | 广度优先 |
| 数据结构 | 栈 | 队列 |
| 空间复杂度 | O(V+E) | O(V+E) |
| 时间复杂度 | O(V+E) | O(V+E) |
| 应用场景 | 连通性检测、环检测、拓扑排序 | 最短路径、最大流、最小割、二分图匹配 |

# 3. 栈在图论中的高级应用

### 3.1 最小生成树（MST）

#### 3.1.1 MST的概念和算法

最小生成树（MST）是一个连通无向图的生成树，其中所有边的权重之和最小。它在图论中有着广泛的应用，例如网络设计、聚类分析和图像分割。

MST算法有两种经典算法：Prim算法和Kruskal算法。

#### 3.1.2 Prim算法和Kruskal算法

**Prim算法**

Prim算法是一种贪心算法，它从图中任意一个顶点出发，逐步添加权重最小的边，直到形成一个生成树。

def prim(graph):
    # 初始化MST
    mst = []

    # 初始化未访问顶点集合
    unvisited = set(graph.vertices)

    # 选择任意一个顶点作为起点
    start_vertex = unvisited.pop()

    # 循环遍历未访问顶点
    while unvisited:
        # 找到与MST中顶点相连的权重最小的边
        min_edge = None
        for vertex in mst:
            for edge in graph.edges[vertex]:
                if edge.destination in unvisited and (min_edge is None or edge.weight < min_edge.weight):
                    min_edge = edge

        # 将最小边添加到MST中
        mst.append(min_edge)

        # 将最小边的终点从未访问顶点集合中移除
        unvisited.remove(min_edge.destination)

    return mst

**Kruskal算法**

Kruskal算法是一种基于并查集的算法，它将图中的所有边按权重从小到大排序，然后依次将边添加到生成树中，直到形成一个生成树。

def kruskal(graph):
    # 初始化MST
    mst = []

    # 初始化并查集
    disjoint_set = DisjointSet()
    for vertex in graph.vertices:
        disjoint_set.make_set(vertex)

    # 将边按权重从小到大排序
    edges = sorted(graph.edges, key=lambda edge: edge.weight)

    # 循环遍历排序后的边
    for edge in edges:
        # 如果边的两个顶点不在同一个集合中，则将边添加到MST中
        if disjoint_set.find_set(edge.source) != disjoint_set.find_set(edge.destination):
            mst.append(edge)

            # 将边的两个顶点合并到同一个集合中
            disjoint_set.union(edge.source, edge.destination)

    return mst

### 3.2 最短路径算法

#### 3.2.1 Dijkstra算法

Dijkstra算法是一种基于贪心思想的最短路径算法，它从起点出发，逐步扩展最短路径，直到到达终点。

def dijkstra(graph, start_vertex):
    # 初始化距离表
    distance =