栈在紧邻排列问题中的解决方案

# 1. 紧邻排列问题概述**

紧邻排列问题是一种组合问题，要求在给定一组元素的情况下，生成所有可能的排列，其中相邻元素必须满足特定条件。例如，在数字排列问题中，相邻数字的差值必须为 1。紧邻排列问题在计算机科学和数学中有着广泛的应用，例如生成密码、解决规划问题和优化算法。

# 2.1 栈的数据结构和操作

### 栈的数据结构

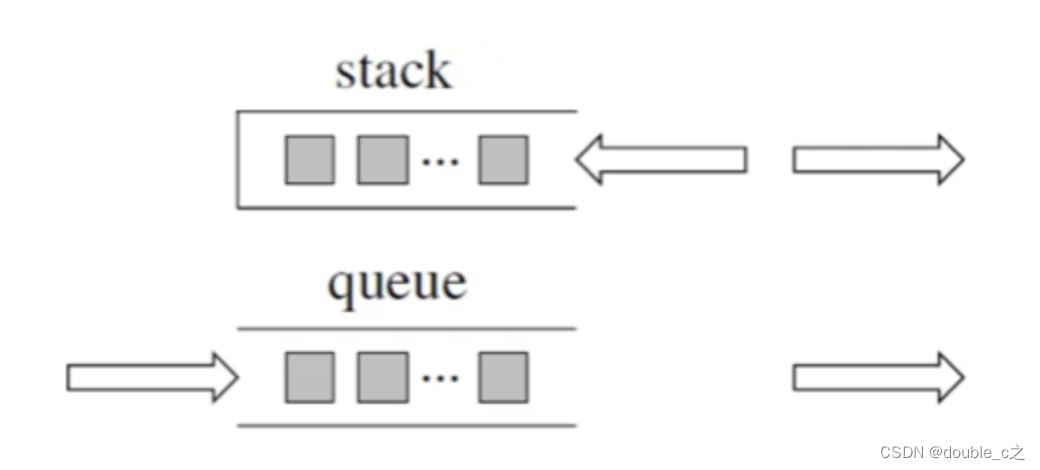
栈是一种线性数据结构，遵循后进先出（LIFO）的原则。它由一系列元素组成，每个元素都存储在一个称为栈帧的内存单元中。栈顶指针指向栈中最后一个元素，即最新添加的元素。

### 栈的操作

栈支持以下基本操作：

- **Push(x)**：将元素 `x` 压入栈顶。
- **Pop()**：移除并返回栈顶元素。
- **Peek()**：返回栈顶元素，但不将其移除。
- **IsEmpty()**：检查栈是否为空。

### 栈的实现

栈可以使用数组或链表实现。数组实现简单高效，但需要预先分配空间。链表实现更灵活，可以动态调整大小，但操作效率稍低。

# 使用数组实现栈
class Stack:
    def __init__(self, size):
        self.stack = [None] * size
        self.top = -1

    def push(self, x):
        if self.top == len(self.stack) - 1:
            raise IndexError("Stack is full")
        self.top += 1
        self.stack[self.top] = x

    def pop(self):
        if self.top == -1:
            raise IndexError("Stack is empty")
        x = self.stack[self.top]
        self.top -= 1
        return x

    def peek(self):
        if self.top == -1:
            raise IndexError("Stack is empty")
        return self.stack[self.top]

    def is_empty(self):
        return self.top == -1

### 代码逻辑分析

上述代码实现了使用数组的栈数据结构。

- `__init__(self, size)`：构造函数，初始化栈并分配指定大小的数组。
- `push(self, x)`：将元素 `x` 压入栈顶，如果栈已满则抛出异常。
- `pop(self)`：移除并返回栈顶元素，如果栈为空则抛出异常。
- `peek(self)`：返回栈顶元素，但不将其移除。
- `is_empty(self)`：检查栈是否为空。

### 参数说明

- `size`：栈的初始大小。
- `x`：要压入栈中的元素。

# 3.1 紧邻排列问题的定义和性质

紧邻排列问题是指，给定一个长度为 n 的序列，找出序列中所有相邻元素之差的绝对值不超过 1 的排列。例如，序列 [1, 2, 3, 4] 有两个紧邻排列：

- [1, 2, 3, 4]
- [2, 1, 3, 4]

而序列 [1, 3, 2, 4] 没有紧邻排列，因为相邻元素 3 和 2 之差为 1。

紧邻排列问题具有以下性质：

- **性质 1：** 序列中所有元素都必须出现。
- **性质 2：** 相邻元素之差的绝对值不超过 1。
- **性质 3：** 紧邻排列的个数与序列中元素的个数 n 相关。

### 3.2 使用栈解决紧邻排列问题的算法

使用栈解决紧邻排列问题是一种递归算法。算法步骤如下：

1. 创建一个栈，并将其初始化为空。
2. 将序列中的第一个元素压入栈中。
3. 对于序列中的每个后续元素：
- 如果栈顶元素与当前元素相等，则将当前元素压入栈中。
- 如果栈顶元素比当