栈在循环依赖检测中的应用

# 1. 栈的基本概念和操作**

栈是一种遵循后进先出（LIFO）原则的线性数据结构。它允许在栈顶进行元素的插入和删除操作。栈的基本操作包括：

- `push(element)`：将元素压入栈顶。
- `pop()`：移除并返回栈顶元素。
- `peek()`：返回栈顶元素，但不移除它。
- `isEmpty()`：检查栈是否为空。

# 2. 循环依赖检测理论基础

循环依赖是一种常见的数据结构问题，它指的是一个数据结构中存在环形引用或依赖关系，导致无法正常遍历或处理数据。循环依赖检测是解决此类问题的关键技术，它可以帮助我们识别和消除循环依赖，确保数据结构的正确性和完整性。

本章将介绍循环依赖检测的理论基础，包括拓扑排序算法和强连通分量算法。这些算法为循环依赖检测提供了有效的解决方案，并广泛应用于软件开发、项目管理和数据挖掘等领域。

### 2.1 拓扑排序算法

#### 2.1.1 拓扑排序的定义和原理

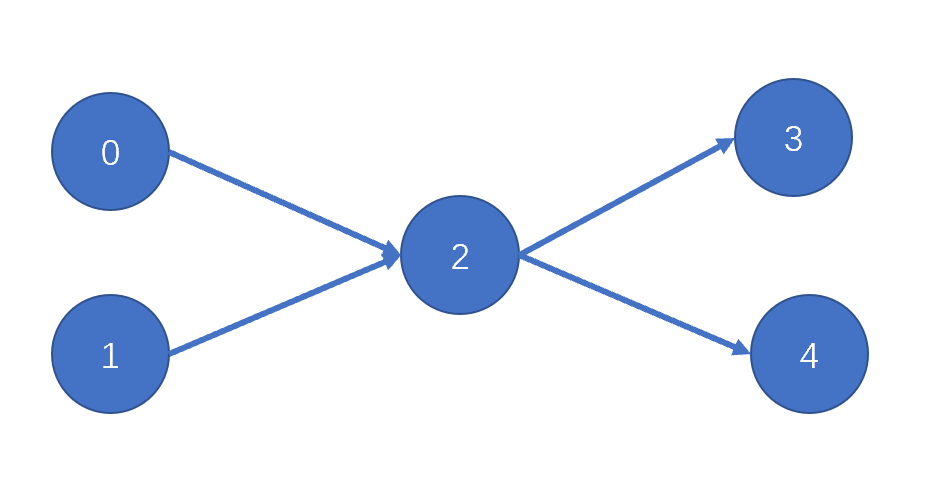
拓扑排序是一种针对有向无环图（DAG）进行排序的算法。DAG 中的节点代表数据项，而有向边代表数据项之间的依赖关系。拓扑排序的目标是找到一个线性序列，使得对于图中任意两个节点 A 和 B，如果 A 指向 B，则 A 在 B 之前出现在序列中。

拓扑排序的原理是基于以下规则：

* 如果一个节点没有入度（即没有其他节点指向它），则将其添加到排序序列的末尾。
* 重复步骤 1，直到所有节点都被添加到序列中或无法找到入度为 0 的节点。

#### 2.1.2 拓扑排序的实现方法

拓扑排序可以通过深度优先搜索（DFS）或广度优先搜索（BFS）算法实现。

**DFS 实现：**

def topological_sort_dfs(graph):
    """
    使用深度优先搜索进行拓扑排序。

    参数：
        graph: 有向无环图，表示为邻接表。

    返回：
        拓扑排序序列。
    """
    visited = set()  # 已访问的节点集合
    stack = []  # 拓扑排序序列

    def dfs(node):
        if node in visited:
            return
        visited.add(node)
        for neighbor in graph[node]:
            dfs(neighbor)
        stack.append(node)

    for node in graph:
        if node not in visited:
            dfs(node)

    return stack[::-1]  # 反转栈以获得拓扑排序序列

**BFS 实现：**

def topological_sort_bfs(graph):
    """
    使用广度优先搜索进行拓扑排序。

    参数：
        graph: 有向无环图，表示为邻接表。

    返回：
        拓扑排序序列。
    """
    in_degree = [0] * len(graph)  # 入度数组
    for node in graph:
        for neighbor in graph[node]:
            in_degree[neighbor] += 1

    queue = [node for node in graph if in_degree[node] == 0]  # 入度为 0 的节点队列
    sorted_list = []  # 拓扑排序序列

    while queue:
        node = queue.pop(0)
        sorted_list.append(node)
        for neighbor in graph[node]:
            in_degree[neighbor] -= 1
            if in_degree[neighbor] == 0:
                queue.append(neighbor)

    return sorted_list

### 2.2 强连通分量算法

#### 2.2.1 强连通分量的定义和性质

强连通分量（SCC）是指有向图中的一组节点，其中任意两个节点之间都存在路径。换句话说，SCC 中的节点相互依赖，无法通过任何顺序排列消除循环依赖。

SCC 的性质包括：

* SCC 中的节点数量至少为 1。
* SCC 中的节点可以相互到达，即对于任意两个节点 A 和 B，存在从 A 到 B 和从 B 到 A 的路径。
* SCC 中的节点无法通过任何顺序排列消除循环依赖。

#### 2.2.2 强连通分量算法的实现

强连通分量算法可以基于 Kosaraju 算法或 Tarjan 算法实现。

**Kosaraju 算法：**

def kosaraju(graph):
    """
    使用 Kosaraju 算法计算强连通分量。

    参数：
        graph: 有向图，表示为邻接表。

    返回：
        强连通分量列表。
    """
    # 第一遍 DFS，得到拓扑排序序列
    visited = set()
    stack = []

    def dfs1(node):
        if node in visited:
            return
        visited.add(node)
        for neighbor in graph[node]:
            dfs1(neighbor)
        stack.append(node)

    for node in graph:
        if node not in visited:
            dfs1(node)

    # 第二遍 DFS，基于拓扑排序序列计算 SCC
    visited = set()
    sccs = []

    def dfs2(node):
        if node in visited:
            return
        visited.add(node)
        sccs[-1].append(node)