栈在回溯算法中的角色与应用

# 1. 栈的基本概念和原理**

栈是一种先进后出（LIFO）的数据结构，它遵循后进先出的原则。元素只能从栈顶添加或删除。栈的底层实现通常是一个数组或链表。

栈的典型操作包括：

- `push(x)`：将元素 `x` 推入栈顶。
- `pop()`：从栈顶移除并返回元素。
- `peek()`：返回栈顶元素，但不移除它。
- `isEmpty()`：检查栈是否为空。

# 2. 栈在回溯算法中的理论基础

### 2.1 回溯算法的原理和应用场景

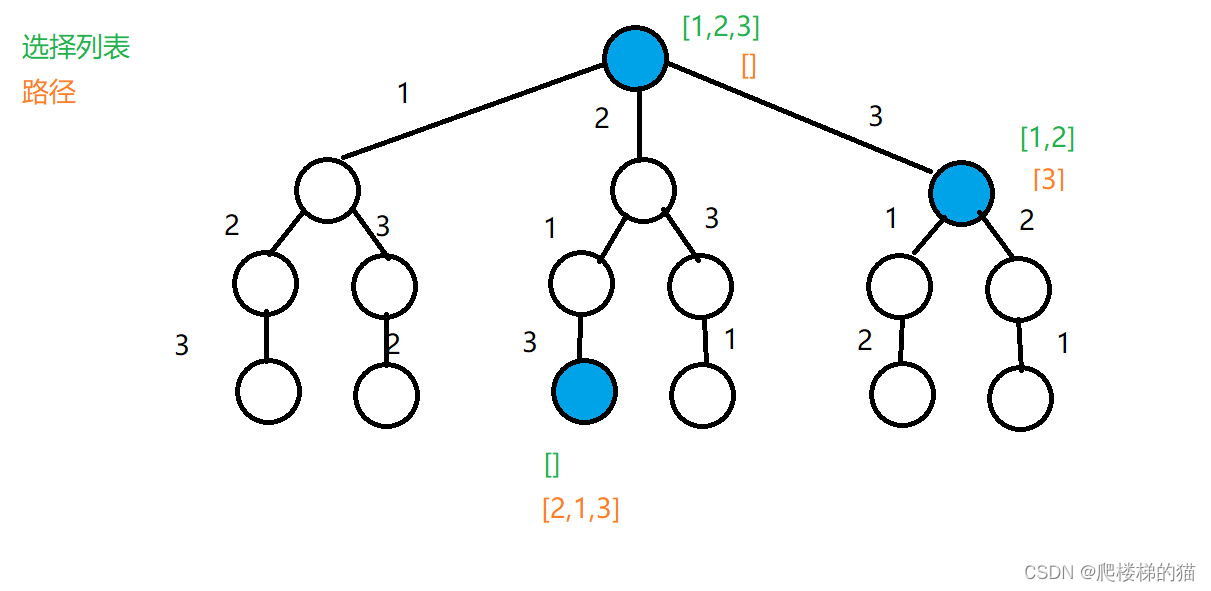
回溯算法是一种深度优先搜索算法，它通过系统地枚举所有可能的解决方案，并逐一检查它们是否满足给定的约束条件，从而找到问题的解。回溯算法的原理如下：

1. **递归调用：**回溯算法将问题分解成一系列子问题，并递归地调用自身来解决每个子问题。
2. **深度优先：**回溯算法首先探索当前子问题的最深层，然后再返回并探索其他子问题。
3. **回溯：**如果当前子问题无法找到可行的解，回溯算法将返回到上一个子问题，并尝试其他可能的解决方案。

回溯算法广泛应用于解决组合优化问题，例如：

* **迷宫求解：**寻找从迷宫入口到出口的路径。
* **八皇后问题：**在 8x8 棋盘上放置 8 个皇后，使得它们互不攻击。
* **图论：**寻找图中的最短路径、最大匹配等。

### 2.2 栈在回溯算法中的作用和机制

栈在回溯算法中扮演着至关重要的角色，它用于存储当前正在探索的子问题和解决方案。具体来说，栈具有以下作用：

* **存储当前状态：**栈存储当前正在探索的子问题的状态，包括当前位置、已经做出的决策等。
* **回溯：**当当前子问题无法找到可行的解时，栈可以帮助回溯到上一个子问题。
* **记录解决方案：**栈可以存储已经找到的可行解决方案，以便在回溯过程中随时访问。

回溯算法使用栈的机制如下：

1. **压栈：**当进入一个新的子问题时，将当前状态压入栈中。
2. **出栈：**当回溯到上一个子问题时，将栈顶元素弹出。
3. **记录解决方案：**当找到一个可行的解时，将该解压入栈中。

通过使用栈，回溯算法可以高效地探索所有可能的解决方案，并找到满足约束条件的解。

# 3.1 栈在迷宫求解中的应用

#### 栈的原理和迷宫求解

栈是一种数据结构，遵循后进先出的原则。在迷宫求解中，栈可以用来存储迷宫中已经探索过的路径。当需要回溯时，栈可以弹出最近探索的路径，从而返回到上一个探索点。

#### 算法步骤

1. 将迷宫的入口点压入栈中。
2. 循环执行以下步骤，直到栈为空或找到出口：
- 从栈顶弹出路径点。
- 检查该路径点是否有未探索的相邻路径。
- 如果有未探索的相邻路径，将该路径点压入栈中并沿着该路径继续探索。
- 如果没有未探索的相邻路径，则该路径点为死胡同，将其从栈中弹出。
3. 如果栈为空，则表示没有找到出口。
4. 如果栈不为空，则栈顶的路径点就是出口。

#### 代码示例

def solve_maze(maze):
    """
    使用栈求解迷宫

    参数：
        maze: 二维列表，表示迷宫，0表示可通行，1表示障碍物

    返回：
        路径列表，表示从入口到出口的路径
    """

    # 定义栈
    stack = []

    # 将入口点压入栈中
    stack.append((0, 0))

    # 循环执行直到栈为空或找到出口
    while stack:
        # 弹出栈顶路径点
        x, y = stack.pop()

        # 检查该路径点是否有未探索的相邻路径
        for dx, dy in [(0, 1), (1, 0), (0, -1), (-1, 0)]:
            nx, ny = x + dx, y + dy
            if 0 <= nx < len(maze) and 0 <= ny < len(maze[0]) and maze[nx][ny