金融行业中的决策树应用：欺诈检测与风险评估

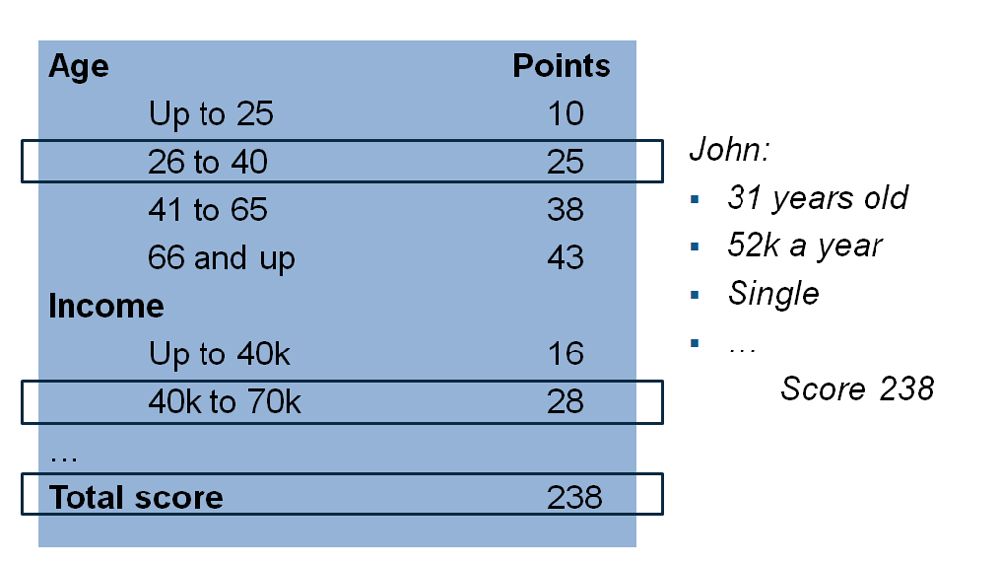
# 1. 决策树基础与金融风险概述

决策树是机器学习领域中一种非常流行的算法，广泛应用于分类和回归问题。本章将带领读者从基础开始，逐步深入理解决策树，并探讨其在金融风险评估中的应用和重要性。

## 1.1 金融风险的定义及其特征

金融风险指的是金融活动中由于不确定性因素导致的潜在损失。其特征包括不确定性、潜在损失、难以预测等。由于金融市场的复杂性，如何有效识别和管理这些风险至关重要。

## 1.2 决策树算法简介

决策树通过模拟人类决策过程，通过一系列的判断规则将数据集分成不同的类别。它在结构上类似于一棵倒置的树，其中每个内部节点代表一个属性上的判断，而每个分支代表一个判断结果的输出。

## 1.3 决策树在金融风险评估中的作用

在金融风险评估中，决策树能够帮助决策者根据历史数据进行模式识别，预测客户违约概率，从而制定相应的风险控制策略。决策树的优势在于模型简单直观，易于理解和解释，这对于需要高度透明度和合规性的金融行业来说尤为重要。

通过对决策树算法和金融风险的初步了解，我们为后续深入探讨决策树的理论基础和实际应用奠定了基础。接下来的章节，我们将深入解析决策树的算法原理，并在金融风险检测和评估中具体应用。

# 2. 决策树算法理论详解

## 2.1 决策树的构建原理

### 2.1.1 信息增益与熵的概念

决策树是一种基本的分类与回归方法。它从数据集中不断进行分割，创建分支结构，直至树的每个叶节点都对应了数据中的一个类别标签。在这个过程中，我们需要理解两个核心概念：熵（Entropy）和信息增益（Information Gain）。

熵是一个衡量数据集混乱度的度量。在信息论中，它描述了一个系统的信息量。如果我们有一组数据集，其中有N个类别标签，那么其熵可以表示为：
\[ E(S) = -\sum_{i=1}^{N} p_i \log_2(p_i) \]
其中，\( p_i \) 是第i类数据在数据集S中出现的概率。

信息增益则描述了分割数据前后，熵的减少量。在选择最佳特征进行分割时，信息增益最大的特征被认为是最佳分割特征。信息增益\( IG(S, A) \)通过以下公式计算：
\[ IG(S, A) = E(S) - \sum_{t \in T} \frac{|S_t|}{|S|} E(S_t) \]
其中，\( E(S) \)是原始数据集S的熵，\( T \)是特征A分割后得到的子集集合，\( S_t \)是子集t中的数据点集合，\( |S_t| / |S| \)是子集t中数据点占总数据点的比例，\( E(S_t) \)是子集t的熵。

### 2.1.2 决策树的分裂标准

在决策树的构建过程中，分裂标准的选择至关重要。分裂标准确定了如何最优地划分特征空间，并决定树的形状。常用的分裂标准有以下几种：

- **信息增益**：基于信息论的原理，选择信息增益最大的特征进行分裂。
- **信息增益比**：考虑了特征个数的影响，优先选择信息增益比高的特征。
- **Gini指数（基尼不纯度）**：衡量随机选取两个数据点，其类别标签不一致的概率。Gini指数越低，数据集的纯度越高。

为了进一步分析这些标准，我们以一个简单的代码示例来说明信息增益的计算过程：

import numpy as np
from collections import Counter

def calculate_entropy(target_col):
    elements, counts = np.unique(target_col, return_counts=True)
    entropy = -np.sum([(counts[i] / np.sum(counts)) * np.log2(counts[i] / np.sum(counts)) for i in range(len(elements))])
    return entropy

def information_gain(data, split_feature_name, target_name):
    total_entropy = calculate_entropy(data[target_name])
    vals, counts = np.unique(data[split_feature_name], return_counts=True)
    Weighted_Entropy = np.sum([(counts[i] / np.sum(counts)) * calculate_entropy(data.where(data[split_feature_name]==vals[i]).dropna()[target_name]) for i in range(len(vals))])
    Information_Gain = total_entropy - Weighted_Entropy
    return Information_Gain

# 示例数据集
data = pd.DataFrame({
    'Outlook': ['Sunny', 'Sunny', 'Overcast', 'Rain', 'Rain', 'Rain', 'Overcast', 'Sunny', 'Sunny', 'Rain', 'Sunny', 'Overcast', 'Overcast', 'Rain'],
    'Temperature': ['Hot', 'Hot', 'Hot', 'Mild', 'Cool', 'Cool', 'Cool', 'Mild', 'Cool', 'Mild', 'Mild', 'Mild', 'Hot', 'Mild'],
    'Humidity': ['High', 'High', 'High', 'High', 'Normal', 'Normal', 'Normal', 'High', 'Normal', 'Normal', 'Normal', 'High', 'Normal', 'High'],
    'Wind': ['Weak', 'Strong', 'Weak', 'Weak', 'Weak', 'Strong', 'Strong', 'Strong', 'Weak', 'Strong', 'Weak', 'Strong', 'Weak', 'Strong'],
    'PlayTennis': ['No', 'No', 'Yes', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'No']
})

# 计算信息增益
information_gain(data, 'Outlook', 'PlayTennis')

在此代码块中，我们计算了基于“Outlook”特征的信息增益。通过计算“Outlook”特征不同取值的条件熵，并将其与整个数据集的熵进行比较，得到信息增益值。

## 2.2 决策树模型的选择与优化

### 2.2.1 常见的决策树算法对比

在构建决策树时，有多种算法可供选择，如ID3、C4.5、C5.0和CART。每种算法在选择分裂特征时依据的分裂标准不同，也各有优势和局限性。

- **ID3**：仅支持离散特征，使用信息增益作为分裂标准。
- **C4.5**：改进自ID3，支持连续特征，并用信息增益比优化了特征选择。
- **C5.0**：C4.5的商业版本，增加了剪枝功能和规则提取功能。
- **CART**：使用基尼指数作为分裂标准，既可以用于分类也可以用于回归。

### 2.2.2 超参数调整与模型剪枝

决策树模型的性能在很大程度上依赖于超参数的选择和模型剪枝策略。超参数包括树的深度、叶子节点的最少样本数、分裂所需的最小样本权重分数等。正确调整这些超参数可以防止模型过拟合或欠拟合。模型剪枝是一种避免过拟合的技术，分为预剪枝和后剪枝。

预剪枝是在训练过程中提前停止树的生长。当树达到某一特定条件时，例如树达到某个深度或者节点中的数据点太少，树的生长就会停止。

后剪枝则是在决策树完全生长之后，通过剪掉那些对于预测结果影响不大的分支，来减少树的复杂度。剪枝过程通常基于验证集的性能，选择剪掉那些可以提升模型验证准确性或减少过拟合风险的分支。

## 2.3 决策树模型的评价指标

### 2.3.1 准确率、召回率与F1分数

评价一个决策树模型的性能，我们通常会关注以下几个指标：

- **准确率**（Accuracy）：正确预测的数据点占总数据点的比例。
- **召回率**（Recall）：正确预测为正例的数据点占实际正例数据点的比例。
- **F1分数**（F1 Score）：准确率和召回率的调和平均值，是一个综合考虑准确率和召回率的指标。

这些指标通过混淆矩阵计算得出。混淆矩阵是一个表格，用于描述分类模型的表现。它将实际标签与预测标签进行对比，形成以下四个部分：

- 真正例（TP）
- 假正例（FP）
- 真负例（TN）
- 假