【如何构建一个基础的diffusion模型】： 探讨如何构建一个基础的diffusion模型

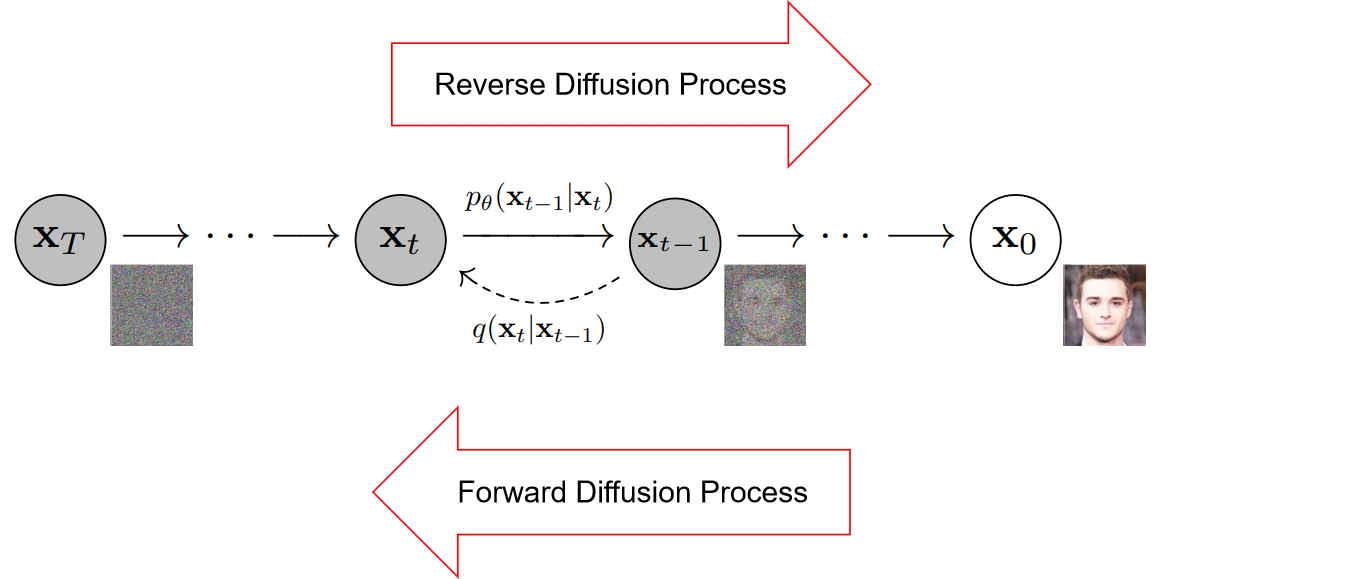
# 1. 理解Diffusion模型基础概念

Diffusion模型是描述物质传输过程的数学模型，其中包含扩散现象的基本特征。在自然界和工程领域中，扩散现象的模拟和预测具有重要意义。Diffusion模型基于质量守恒和Fick定律，描述了物质在浓度梯度下的传播规律。通过理解扩散模型的基础概念，可以更好地应用数学原理进行模型推导和编程实现，进而解决各种实际问题。在分析扩散模型时，需考虑扩散系数、初始条件和边界条件等因素的影响，以全面理解和应用Diffusion模型。

# 2. 数学原理与方程推导

### 2.1 简单扩散方程及其意义
扩散过程在自然界中无处不在，而数学是描述这些过程的重要工具之一。简单的一维扩散方程可以由以下偏微分方程表示：

\frac{\partial u}{\partial t} = D \cdot \frac{\partial^2 u}{\partial x^2}

其中，$u(x,t)$ 是描述扩散物质浓度随空间 $x$ 和时间 $t$ 的变化；$D$ 是扩散系数，描述了物质扩散的速率。

#### 2.1.1 对扩散过程的数学描述
扩散过程的数学描述在不同领域有着广泛的应用。通过扩散方程，可以研究物质在空间上的传播和浓度分布变化。这对于环境科学、生物学等领域的研究具有重要意义。

#### 2.1.2 扩散系数的定义与影响因素
扩散系数 $D$ 受到多种因素影响，如温度、环境介质、物质性质等。在具体建模时，需要根据实际情况合理选择扩散系数的数值，以准确描述扩散过程。

### 2.2 离散扩散模型的建立
在实际计算中，往往需要将连续的扩散方程转化为离散形式，方便计算机实现。

#### 2.2.1 空间离散化方法分析
离散化方法的选择对模型的准确性和计算效率有着重要影响。常见的方法包括有限差分、有限元等，不同方法适用于不同的情况。

#### 2.2.2 时间步长的选取与稳定性分析
在离散化过程中，时间步长的选取需要考虑数值稳定性。通过稳定性分析可以确定最大时间步长，保证模拟结果的准确性和稳定性。

### 2.3 边界条件的处理与影响
边界条件在扩散模型中起着至关重要的作用，不同的边界条件会对模型结果产生显著影响。

#### 2.3.1 不同边界条件对模型结果的影响
常见的边界条件包括固定浓度、固定通量、周期性边界等。在模拟过程中，需要根据实际情况选择合适的边界条件。

#### 2.3.2 边界条件处理的常见方法
针对不同的边界条件，可以采用不同的处理方法，如人工设定边界条件、采用特殊插值方法等。合理处理边界条件可以提高模型的准确性和可靠性。

通过对数学原理与方程推导的深入理解，我们可以更好地建立扩散模型并进行模拟计算，为实际问题的解决提供可靠的数值基础。

# 3. 编程实现Diffusion模型

## 3.1 选择合适的编程语言与工具

在实现Diffusion模型时，选择合适的编程语言与工具对于提高开发效率和计算性能至关重要。本节将介绍两种常用的编程语言及工具，分别是Python和MATLAB，并探讨它们在Diffusion模型实现中的优势。

### 3.1.1 Python及其科学计算库的优势

Python作为一种优秀的通用编程语言，拥有丰富的科学计算库，如NumPy、SciPy和Matplotlib，适用于复杂的数值计算和数据可视化任务。使用Python实现Diffusion模型具有以下优势：

- **便捷易学**：Python语法简洁清晰，易于上手和学习，适合编写复杂算法。
- **丰富库支持**：NumPy提供了高效的数组操作，SciPy包含了各种科学计算工具，Matplotlib用于绘制图表，三者协同工作，能够快速实现Diffusion模型。
- **开源社区活跃**：Python拥有庞大的开源社区，用户可以方便地获取各种开源代码和工具，加速开发进程。

下面是使用Python实现简单的Diffusion模型的代码示例：

import numpy as np
import matplotlib.pyplot as plt

# 模拟Diffusion模型
def diffusion_model(initial_state, num_steps, diffusion_rate):
    state = initial_state
    for _ in range(num_steps):
        new_state = np.zeros_like(state)
        fo