【diffusion模型中常见的数学方程解释】： 解释diffusion模型中常见的数学方程

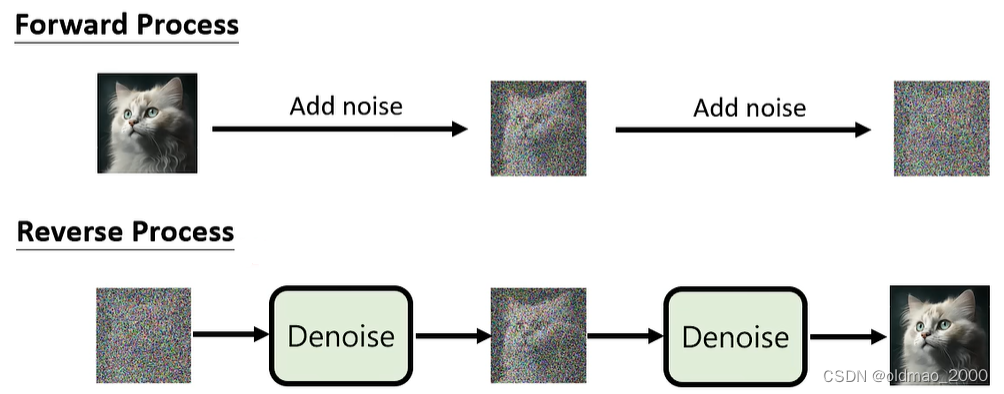
# 1. 了解Diffusion模型

Diffusion模型是一种描述物质扩散和传播过程的数学模型。在科学研究和工程应用中具有广泛的应用，涉及领域包括生物学、物理学、经济学等。Diffusion模型的核心思想是通过描述物质在空间上的变化过程来分析散播规律，通常采用概率密度函数、随机微分方程和偏微分方程等工具进行建模和求解。

在了解Diffusion模型的过程中，不仅需要理解其基本概念，还需要掌握其数学推导和实际应用。通过对Diffusion模型的深入研究，可以更好地理解物质传播行为，为相关领域的研究与应用提供理论支撑。

# 2. 数学方程基础知识

### 2.1 概率密度函数 (PDF)

#### 2.1.1 概念解析
概率密度函数（Probability Density Function，简称PDF）是概率论中的重要概念，用于描述随机变量在各个取值点上的概率密度情况。在数学上，概率密度函数通常表示为$f(x)$，其中$x$为随机变量的取值。PDF满足以下两个条件：1）$f(x)\geq0$，即非负性；2）$\int_{-\infty}^{+\infty}f(x)dx=1$，即概率的总和为1。

#### 2.1.2 PDF在Diffusion模型中的作用
在Diffusion模型中，概率密度函数扮演着至关重要的角色。 Diffusion过程中的随机变量变化可以通过PDF来描述，从而进一步分析扩散的规律和特性。通过对PDF的分析，可以更好地理解扩散现象，并为后续的数学建模奠定基础。

#### 2.1.3 数学推导与应用
为了更深入地理解PDF在Diffusion模型中的作用，我们可以进行数学推导和实际应用。我们可以通过不同的数学方法，比如积分、微分等，来推导PDF的具体形式，并结合具体的Diffusion模型案例进行应用分析，进一步说明PDF对于Diffusion模型的重要性。

在实际代码示例中，我们可以通过Python来实现对PDF的计算和可视化，以加深对PDF概念在Diffusion模型中应用的理解。

import numpy as np
import matplotlib.pyplot as plt

# 生成正态分布的概率密度函数
x = np.linspace(-5, 5, 1000)
pdf = (1/np.sqrt(2*np.pi)) * np.exp(-0.5*x**2)

plt.plot(x, pdf)
plt.title('Normal Distribution PDF')
plt.xlabel('x')
plt.ylabel('Probability Density')
plt.show()

以上代码展示了如何生成并绘制正态分布的概率密度函数，进一步帮助理解PDF在Diffusion模型中的应用。

### 2.2 随机微分方程 (SDE)

#### 2.2.1 SDE概述
随机微分方程（Stochastic Differential Equation，简称SDE）是描述随机过程中随机变量变化的微分方程。SDE在金融学、物理学、生物学等领域中具有广泛应用，尤其在描述Diffusion过程中起到关键作用。

#### 2.2.2 SDE在Diffusion模型中的应用
在Diffusion模型中，SDE常常被用来描述随机变量的演化，特别是在涉及到扩散现象的过程中。通过建立适当的SDE模型，可以更准确地模拟和预测扩散过程中的随机性特征，从而更好地理解和分析Diffusion现象。

#### 2.2.3 解析求解SDE
解析求解SDE是一个重要且具有挑战性的问题，针对不同的SDE形式存在多种求解方法。在实际应用中，可以通过变换、积分等方法对SDE进行求解，从而得到关于随机过程的具体解析表达式。

#### 2.2.4 模拟求解SDE
除了解析方法，模拟求解SDE也是一种常见的求解方式。通过数值模拟方法（如蒙特卡洛模拟），可以对SDE进行仿真求解，得到随机过程的近似解，并用于对Diffusion现象的研究和分析。

在实际代码实现中，我们可以使用Python的数值计算库（如NumPy）和随机过程模拟库（如SciPy）来模拟求解SDE。下面是一个简单的例子：

import numpy as np

# 模拟求解随机微分方程
def simulate_sde(num_steps, dt):