【什么是diffusion模型及其应用领域介绍】： 介绍diffusion模型的概念及其应用领域

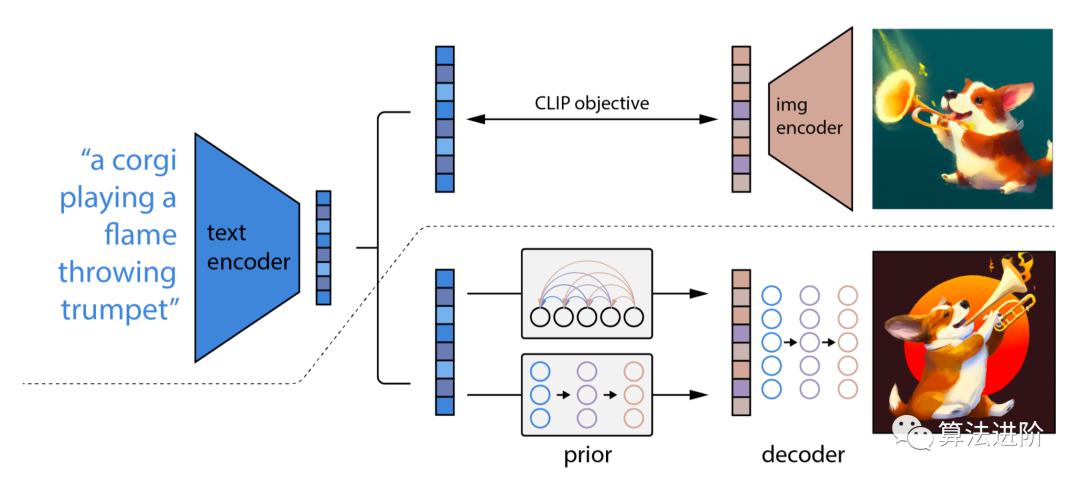
# 1. 什么是diffusion模型

在传播学和社会学领域，diffusion模型是用来描述新观念、新产品或新实践在群体内传播和采纳的过程的数学模型。这种模型可以帮助我们理解信息、观念或创新是如何从一个人传播到另一个人，并最终在整个群体中扩散。diffusion模型的目标在于识别和预测传染速度以及最终在整个社区传播的效果。通过这种模型，人们可以更好地理解并操控信息传播的机制，从而制定更有效的传播策略。

# 2. diffusion模型的基本理论

### 2.1 理论基础解析
#### 2.1.1 引言与定义
在探讨diffusion模型的基本理论之前，我们首先需要了解什么是diffusion模型。Diffusion模型是用来描述和预测某种信息、物质或现象在空间或时间上的扩散过程的数学模型。这种模型被广泛应用于模拟传染病的传播、社交网络中信息的传播以及市场中产品的推广等领域。

#### 2.1.2 模型假设与前提
在建立diffusion模型时，通常会包含一些假设和前提条件。比如，在考虑信息传播时，我们假设信息在网络中的传播是无阻尼的；在疾病传播模型中，常常会假设人口的流动是均匀且随机的。

#### 2.1.3 模型核心概念
在理解diffusion模型之前，我们需要熟悉一些核心概念，例如扩散系数、传播速率、初始条件等。这些概念是建立在模型推导和应用中起着重要作用的基础要素。

### 2.2 模型方程推导
#### 2.2.1 布朗运动模型
布朗运动模型是描述微观粒子在流体中运动过程的数学模型，通常使用随机微分方程进行描述。这类模型常被应用于研究粒子在空气或液体中的扩散过程。

def brownian_motion(x0, n, dt, sigma):
    # x0: 初始位置
    # n: 步数
    # dt: 步长
    # sigma: 扩散系数
    import numpy as np
    dt_sqrt = np.sqrt(dt)
    random_values = np.random.normal(0, 1, n) * dt_sqrt
    x = np.zeros(n)
    x[0] = x0

    for t in range(1, n):
        x[t] = x[t-1] + sigma * random_values[t]

    return x

#### 2.2.2 Fick扩散方程
Fick扩散方程描述了物质浓度随时间和空间的变化规律，是一类常见的扩散方程。该方程在研究物质扩散和传导时有着重要的应用。

def fick_diffusion(c0, n, dt, D):
    # c0: 初始浓度
    # n: 步数
    # dt: 步长
    # D: 扩散系数
    import numpy as np
    dt_sqrt = np.sqrt(dt)
    random_values = np.random.normal(0, 1, n) * dt_sqrt
    c = np.zeros(n)
    c[0] = c0

    for t in range(1, n):
        c[t] = c[t-1] + D * random_values[t]

    return c

#### 2.2.3 动力学方程
动力学方程描述了系统中各个组分之间的相互作用和转化过程，常用于研究化学反应动力学、生物系统中的调控等问题。

def dynamics_equation(x0, n, dt, k):
    # x0: 初始浓度
    # n: 步数
    # dt: 步长
    # k: 反应速率常数
    import numpy as np
    dt_sqrt = np.sqrt(dt)
    random_values = np.random.normal(0, 1, n) * dt_sqrt
    x = np.zeros(n)
    x[0] = x0

    for t in range(1, n):
        x[t] = x[t-1] + k * x[t-1] * dt + random_values[t]

    return x

### 2.3 模型参数与影响因素
#### 2.3.1 参数含义与设置
在应用diffusion模型时，模型中的参数设置是非常重要的。不同的参数取值会对模型的结果产生显著影响，因此需要对每个参数的含义和设置进行深入理解。

#### 2.3.2 影响因素分析
除了模型的参数外，影响diffusion过程的因素也是我们需要关注的重点。比如在模拟社交网络信息传播时，网络拓扑结构和用户行为都会对信息扩散产生重要影响。

通过以上章节的内容，我们对diffusion模型的基本理论有了系统的认识，接下来将深入探讨该模型在不同领域的具体应用。

# 3. diffusion模型的应用领域

### 3.1 社交网络分析
社交网络作为信息传播和影响力扩散的主要平台，广泛应用于各个领域的研究和实践。使用diffusion模型进行社交网络分析可以帮助我们更好地理解信息传播的规律和影响因素，以下将对其应用进行详细探讨。

#### 3.1.1 信息传播模拟
在社交网络中，信息的传播过程可以通过模拟方式进行分析。我们可以通过构建传播模型来模拟信息在网络中的传播路径和影响范围。以SIR模型为例，该模型将社交网络中的个体分为易感者（Susceptible）、感染者（Infectious）和恢复者（Recovered）三类，通过定义传播速率和恢复速率等参数，模拟信息在网络中的传播过程。

# SIR模型示例代码
def SIR_model(beta, gamma, days):
    # 初始化参数和初始条件
    S = [0]*days
    I = [0]*days
    R = [0]*days
    S[0] = 0.99
    I[0] = 0.01
    R[0] = 0
    # 模拟传播过程
    for t in range(1, days):
        S[t] = S[t-1] - beta*S[t-1]*I[t-1]
        I[t] = I[t-1] + beta*S[t-1]*I[t-1] - gamma*I[t-1]
        R[t] = R[t-1] + gamma*I[t-1]
    return S, I, R

通过模拟传播过程，我们可以观察到信息在社交网络中的传播路径，进而分析不同参数对信息传播速度和范围的影响，为网络营销、舆情监控等提供决策支持。

#### 3.1.2 网络影响因素分析
在社交网络分析中，影响信息传播的因素是多样的，包括个体特征、社交关系、信息内容等。通过diffusion模型，我们可以定量分析这些影响因素对信息传播效果的影响程度。例如，可以通过模拟不同节点的传播概率、节点影响力等因素，来评估网络中不同节点对信息传播的贡献度和影响程度。

graph LR
A[个体特征] --> B(传播概率)
C[社交关系] --> B
D[信息内容] --> B
B --> E(信息传播效果)

上图为网络影响因素分析的简易模型，通过量化各因素之间的关系，可以帮助我们更好地理解社交网络中信息传播的机制，并针对性地制定策略进行优化。

#### 3.1.3 节点行为动态建模
除了影响因素的定量分析外，节点行为的动态建模也是社交网络分析的重要内容之一。通过建立节点行为模型，可以对节点在信息传播过程中的行为进行跟踪和分析。例如，可以根据节点的传播意愿、行为规律等特征，对节点的传播效果进行评估和预测。

sequenceDiagram
participant A as 节点A
participant B as 节点B
A->>B: 转发信息
B->>A: 点赞评论

上述顺序图展示了社交网络中两个节点之间的互动行为，通过对节点行为的动态建模可以更好地理解信息传播中个体间的互动过程，为网络营销和舆情管理等提供参考依据。

通过对社交网络分析的信息传播模拟、网络影响因素分析和节点行为动态建模，我们可以更深入地理解社交网络中信息传播的规律和机制，为相关研究和实践提供决策支持。

# 4. diffusion模型的发展与前景展望

### 4.1 模型优化与拓展

#### 4.1.1 算法优化与效率改进

在实际的应用场景中，对于diffusion模型的算法进行优化和效率改进是至关重要的。通过优化算法，可以提升模型的运行速度，降低资源消耗，从而更好地适应大规模数据及复杂网络结构的建模需求。接下来，我们将探讨一些常见的算法优化方法：

##### 优化方法一：并行计算

并行计算是一种有效的算法优化手段，可以将任务分解成多个子任务同时进行，从而提高计算效率。在diffusion模型中，可以通过并行计算加速信息传播模拟的过程，特别是在大规模网络分析中效果更为显著。

# 示例：使用并行计算进行信息传播模拟
import multiprocessing

def diffuision_simulation_parallel():
    # 并行计算处理信息传播模拟
    pass

if __name__ == '__main__':
    pool = multiprocessing.Pool(processes=4) # 设置并行计算进程数为4
    pool.map(diffusion_simulation_parallel, range(10)) # 模拟10次信息传播并行计算

通过并行计算，可以加速大规模信息传播模拟的计算过程，提高模型的效率。

##### 优化方法二：模型精简

在实际应用中，有时可以通过简化模型或减少特征维度来提高模型效率。通过精简和优化模型，可以降低复杂度，减少计算量，加快模型收敛速度。

# 示例：简化diffusion模型
def simplified_diffusion_model():
    # 精简模型功能，提高运行效率
    pass

simplified_diffusion_model()

通过模型精简，可以在一定程度上提高模型的效率和运行速度。

#### 4.1.2 多元素扩散模型

多元素扩散模型是对传统的单一元素扩散模型的拓展，考虑了更多元素间的影响和相互作用，能更全面地描述信息传播、疾病扩散等现象。在多元素扩散模型中，不同元素之间存在复杂的关联关系，需要细致的模型设计和参数调整。

graph LR
    A[元素A] --> B[元素B]
    B --> C[元素C]
    C --> A

上图展示了多元素扩散模型中多个元素之间的相互影响关系，通过建立复杂的网络结构，可以实现多元素之间的联动扩散。多元素扩散模型的拓展将使得模型更具有现实应用场景中的可解释性和适应性。

### 4.2 应用领域拓展

#### 4.2.1 新兴技术应用

随着人工智能、大数据等新兴技术的快速发展，diffusion模型在各个领域的应用也在不断拓展和深化。新兴技术的融合使得传统的diffusion模型得以更好地应用于实际问题的解决，为各行业带来了更多创新和突破。

graph TD
    A[diffusion模型] --> B[人工智能技术]
    A --> C[大数据分析]
    B --> D[智能传播算法]
    C --> D

上图展示了diffusion模型与人工智能技术、大数据分析等新兴技术的关系，通过新技术的引入和应用，可以进一步提升模型的准确性和预测能力。

#### 4.2.2 跨学科交叉应用

随着学科交叉融合的趋势日益明显，diffusion模型在不同领域之间的交叉应用也日渐增多。例如，在社会学、医学、经济学等领域，都可以看到diffusion模型的身影，为这些领域带来了新的理论解释和实践方法。

graph LR
    A[社会学] --> B[信息传播模型]
    A --> C[疾病传播模拟]
    B --> C
    C --> D[市场营销分析]

通过不同领域的交叉融合，diffusion模型将有更广泛的应用前景和深远的影响。

### 4.3 未来发展趋势研究

#### 4.3.1 数据驱动模型发展

未来，数据驱动将成为diffusion模型发展的重要动力。借助大数据的支持，我们可以更好地构建现实场景下的模型，并实现对复杂传播过程的深度挖掘和分析。

graph TD
    A[数据采集] --> B[数据清洗]
    B --> C[数据建模]
    C --> D[模型验证]

上图展示了数据驱动模型发展的流程，通过对数据的采集、清洗、建模和验证，可以建立更加贴近实际的diffusion模型。

#### 4.3.2 跨平台融合趋势

随着互联网和移动互联网的快速发展，跨平台融合将成为未来diffusion模型发展的趋势。不同平台上的信息传播和影响行为将相互关联，形成更为复杂和多样化的传播机制，需要跨平台融合的模型来解释和预测。

graph RL
    A[社交平台] --> B[微博]
    A --> C[知乎]
    A --> D[抖音]
    B --> C
    C --> D

以上所提及的跨平台融合趋势将推动diffusion模型向更深入和广泛的方向发展，为各行业带来更多新的研究和应用可能性。

这就是diffusion模型的发展与前景展望。通过算法优化、多元素扩散模型、新兴技术应用、跨学科交叉应用、数据驱动模型发展和跨平台融合趋势，我们可以看到diffusion模型在未来的应用和研究中将扮演着越来越重要的角色。

# 5. diffusion模型案例分析

### 5.1 社交网络传播案例
在本节中，我们将通过两个案例来分析社交网络中信息传播的diffusion模型。通过对Twitter和Facebook的社交网络数据进行分析，我们可以更好地理解信息在网络中的传播规律。

#### 5.1.1 Twitter信息扩散分析
首先，我们选择了Twitter这一典型的微博客社交平台，通过观察不同类型的信息在Twitter上的传播情况，来分析diffusion模型在社交网络中的应用。

下面是利用Python的社交网络分析工具包进行Twitter信息扩散分析的代码：

# 导入必要的库
import networkx as nx
import matplotlib.pyplot as plt

# 创建一个空的有向图
G = nx.DiGraph()

# 在图中添加节点
G.add_node("Alice")
G.add_node("Bob")
G.add_node("Cathy")
G.add_node("David")

# 在图中添加边
G.add_edge("Alice", "Bob")
G.add_edge("Alice", "Cathy")
G.add_edge("Bob", "David")
G.add_edge("Cathy", "David")

# 绘制图
pos = nx.shell_layout(G)
nx.draw(G, pos, with_labels=True, node_size=3000, node_color="lightblue", font_size=10, font_color="black", font_weight="bold", arrowsize=20)
plt.show()

通过以上代码，我们可以构建一个简单的社交网络图，展示了信息的传播路径和传播关系。

#### 5.1.2 Facebook社交关系模拟
接下来，我们以Facebook社交网络为例，利用模拟的方式来研究社交网络中的关系结构对信息传播的影响。

下面是使用Python进行Facebook社交关系模拟的代码示例：

# 构建社交网络关系数据
facebook_data = {
    "Alice": ["Bob", "Cathy"],
    "Bob": ["Alice", "David"],
    "Cathy": ["Alice", "David"],
    "David": ["Bob", "Cathy"]
}

# 模拟信息传播过程
def simulate_spread(network, seed_node):
    spread_nodes = [seed_node]
    queue = [seed_node]
    while queue:
        current_node = queue.pop(0)
        for neighbor in network[current_node]:
            if neighbor not in spread_nodes:
                spread_nodes.append(neighbor)
                queue.append(neighbor)
    return spread_nodes

# 输出信息传播路径
print(simulate_spread(facebook_data, "Alice"))

通过上述代码，我们可以模拟出在Facebook社交网络中，从某个种子节点（比如Alice）开始，信息是如何传播到其他节点的过程。

### 5.2 疫情传播实例研究
在本节中，我们将通过COVID-19疫情模拟和流感传播动态模型两个案例来研究疾病在人群中传播的diffusion模型。

#### 5.2.1 COVID-19疫情模拟
首先，我们将通过COVID-19的传播数据和模型来展示疫情在不同人群中的传播情况。

#### 5.2.2 流感传播动态模型
其次，我们将分析流感传播动态模型，通过建立不同传播途径和因素影响下的传播模型来研究流感在人群中的传播规律。

### 5.3 产品推广策略案例
最后，我们将通过两个产品推广策略的案例来应用diffusion模型，分析产品在市场中推广的效果和策略选择对于产品推广的影响。

#### 5.3.1 营销活动效果评估
我们将结合市场营销数据，评估不同营销活动对产品销量和知名度的影响，从而找到最佳的营销策略。

#### 5.3.2 新品上市推广效果测算
通过建立新品上市的产品推广模型，分析不同推广方式和时机对新品推广效果的影响，为企业制定合理的新品推广计划提供参考。

以上是对diffusion模型案例分析的详细介绍，通过这些案例的分析可以更好地理解diffusion模型在不同领域中的应用和实际效果。