【掌握在实际场景中如何搭建更复杂的diffusion模型】： 掌握在实际场景中如何搭建更复杂的diffusion模型

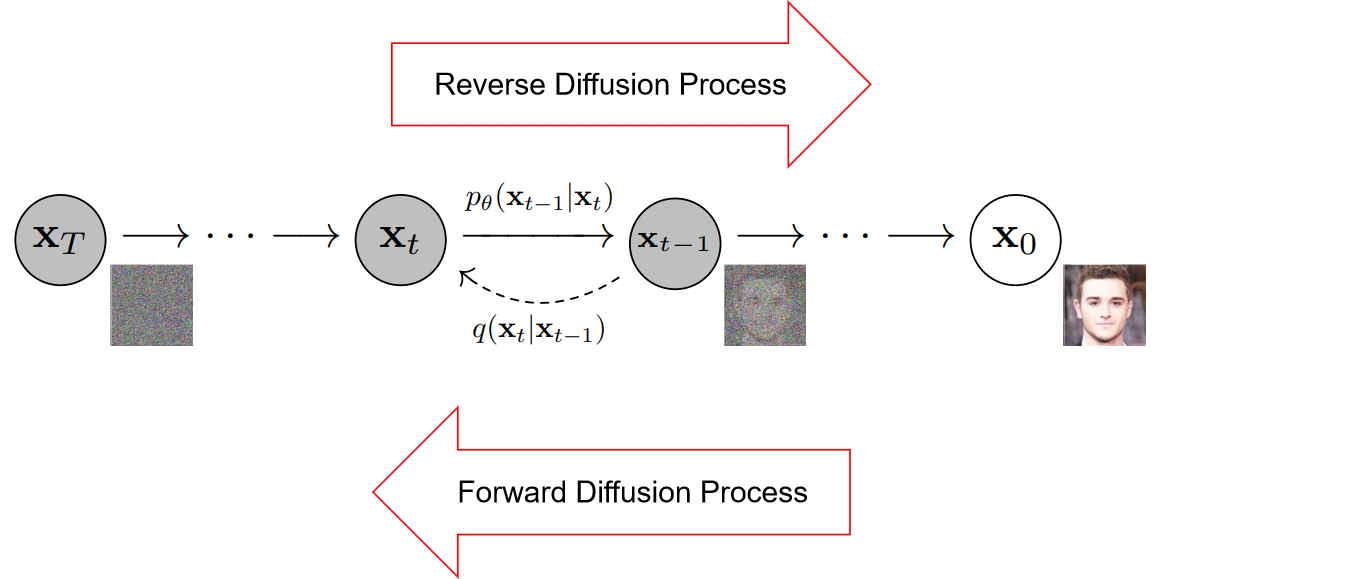
# 1. 理解Diffusion模型

Diffusion模型是一种用来描述信息、创新等在人群中传播过程的数学模型。在实际应用中，Diffusion模型可以帮助我们理解产品在市场中传播的方式和规律，从而指导市场营销策略的制定。通过对人群关系、传播速度等因素的分析，我们可以更好地把握产品传播的路径和效果，提高营销效益。

而在文章中，深入探讨Diffusion模型的原理、作用及应用领域，将有助于读者更全面地理解这一模型的重要性和实际应用意义。

# 2.1 分析Diffusion的概念

Diffusion是指一种在社会学、市场营销与传播学中常见的概念，它描述了信息、创新或产品在人群中传播和接受的过程。通过对Diffusion的概念进行分析，我们可以更好地理解它在实际场景中的作用以及应用领域。

### 2.1.1 了解Diffusion在实际场景中的作用

Diffusion在实际场景中扮演着至关重要的角色，它影响着产品、服务或想法的传播速度和范围。当一个新的创新出现时，它需要通过Diffusion的过程才能被更多的人接受和采纳。Diffusion有助于推动社会的变革与发展，也对市场的竞争与演变产生深远影响。

在市场营销中，了解Diffusion的作用可以帮助企业更好地制定推广策略，抓住市场先机，提高产品的市场渗透率。同时，在学术研究与实践中，对Diffusion的作用有助于深入探讨信息传播与影响力扩散的机制。

### 2.1.2 探索Diffusion模型的应用领域

Diffusion模型的应用涵盖了多个领域，例如社会网络分析、消费者行为研究、产品创新与营销策略等。通过建立Diffusion模型，可以帮助我们更好地理解信息传播的规律，预测产品或创新的市场接受程度，并优化推广策略。

在社会网络分析中，Diffusion模型被广泛运用于研究信息在网络中的传播路径与效应，从而识别关键意见领袖与影响力节点。在产品创新领域，Diffusion模型则被用来评估新产品的市场推广效果，指导产品的定位与推广策略制定。

总的来说，深入探索Diffusion模型的应用领域可以为我们提供更多的思路与方法，帮助我们更好地应对不同场景下的信息传播与影响力扩散挑战。

# 3. 搭建更复杂的Diffusion模型

### 3.1 深入研究Diffusion模型的扩展
Diffusion模型作为一种传播模型在实际场景中有着广泛的应用，但在某些情况下，需要考虑更复杂的因素来构建模型以更好地拟合真实情况。在这一节，我们将深入研究如何扩展Diffusion模型，以应对更加复杂的传播情形。

#### 3.1.1 探讨如何增加Diffusion模型的复杂度
在实际情况下，传播过程可能受到多种因素的影响，比如社交关系、地理位置、时间等。为了更准确地描述信息、疾病、观念传播的过程，需要将这些因素纳入模型考虑范畴。我们可以通过引入不同的权重系数、节点属性、边的类型等来增加模型的复杂度，从而更好地捕捉现实场景中的传播特点。

# 示例代码：增加社交关系因素的扩展Diffusion模型
def c