【利用diffusion模型解决实际业务中的扩展问题】： 利用diffusion模型解决实际业务中的扩展问题

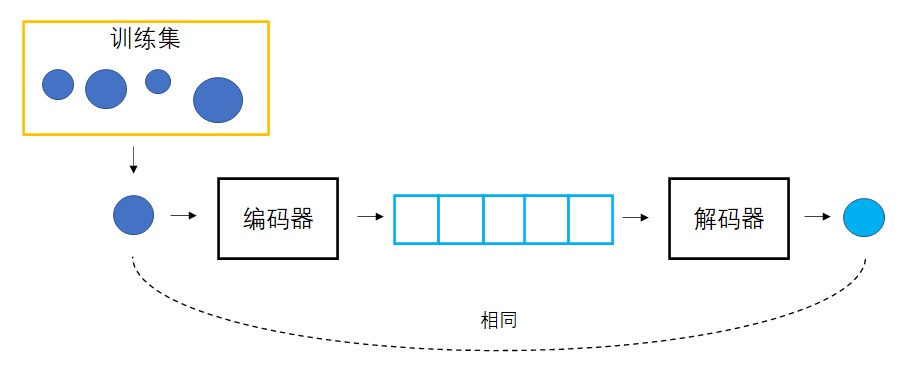
# 1. 理解Diffusion模型

Diffusion模型是一种用于描述信息、创新、产品等在人群或网络中传播和扩散的数学模型。该模型通过模拟人群之间的相互影响和信息传递过程，帮助我们理解和预测扩展问题的发展趋势。在实际应用中，Diffusion模型对于预测市场营销、社交网络传播、疾病传播等具有重要意义。通过深入理解Diffusion模型的原理和机制，我们可以更好地应用这一技术解决复杂的扩展问题，实现更有效的信息传播和影响力扩大。

# 2. Diffusion模型在实际业务中的应用

### 2.1 了解实际业务中的扩展问题
在探讨Diffusion模型在实际业务中的应用之前，首先需要深入了解实际业务中所面临的扩展问题。这些问题往往涉及到信息、产品、服务等在群体中的传播和影响扩散。让我们一起来了解这些扩展问题的定义和特征。

#### 2.1.1 定义和特征
扩展问题是指在一个群体中，信息、产品或服务从一个节点开始传播，经过一定的传播路径，最终影响到更多的节点的过程。这种传播的特征在于具有连锁反应的效应，即初始的信息扩散会引发更多节点的参与和反馈。

#### 2.1.2 影响扩展问题的因素
在实际业务中，影响扩展问题的因素多种多样。其中，包括但不限于传播速度、传播渠道、群体关系等因素。这些因素相互作用，共同影响着信息传播的效果和范围。

### 2.2 引入Diffusion模型
针对实际业务中的扩展问题，Diffusion模型提供了一种理论和方法来解决信息传播和影响扩散的挑战。在这一部分，我们将探讨如何将Diffusion模型应用于实际业务中。

#### 2.2.1 Diffusion模型概述
Diffusion模型是一种描述信息传播和扩散过程的数学模型。它通常基于网络结构和节点之间的相互影响，来模拟信息的传播路径和影响范围。Diffusion模型可以帮助我们理解和预测信息在群体中的传播效果。

#### 2.2.2 如何将Diffusion模型应用于实际业务
将Diffusion模型应用于实际业务需要结合具体的业务场景和数据特征。通过建立合适的模型，分析数据，调整参数，可以更好地解决实际业务中的扩展问题。下一步，我们将深入探讨Diffusion模型是如何解决扩展问题的原理。

### 2.3 Diffusion模型解决扩展问题的原理
要深入理解Diffusion模型在实际业务中的应用，需要掌握它解决扩展问题的原理。在这一部分，我们将详细介绍扩散过程和网络结构与扩展问题的关系。

#### 2.3.1 扩散过程
Diffusion模型中的扩散过程指的是信息或影响从一个节点传播到相邻节点的过程。这个过程可以通过数学模型来描述，从而推断传播路径和扩展影响。

#### 2.3.2 网络结构与扩展问题的关系
网络结构在Diffusion模型中起着至关重要的作用。不同的网络结构会影响信息传播的速度、范围和效果。通过分析网络结构，可以更好地理解信息扩散的规律和特点。

通过对Diffusion模型解决扩展问题的原理进行深入剖析，我们可以更好地应用这一模型来解决实际业务中的扩展难题。随着对Diffusion模型的理解不断加深，我们可以进一步探讨如何在实践中应用这一模型进行数据分析和预测。

#