卡尔曼滤波MATLAB实战指南：从零基础到精通算法设计

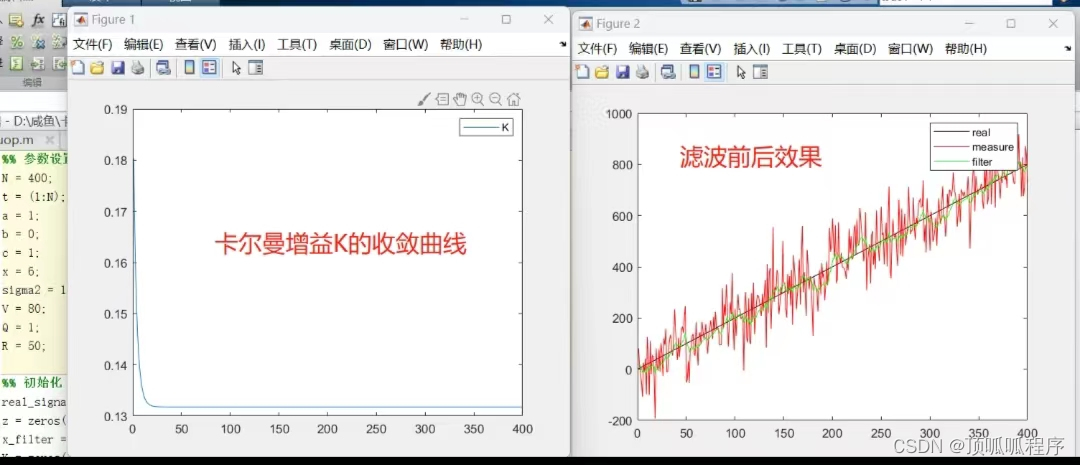
# 1. 卡尔曼滤波理论基础

卡尔曼滤波是一种递归估计算法，用于从一系列测量值中估计动态系统的状态。它广泛应用于各种领域，包括目标跟踪、传感器融合和控制系统。

卡尔曼滤波的基本原理是将系统状态表示为一个状态向量，并使用测量值来更新状态向量的估计值。该算法由两个主要步骤组成：预测更新和测量更新。

在预测更新步骤中，系统状态根据系统动力学模型进行预测。在测量更新步骤中，测量值被用来更新状态估计值，以减少预测误差。

# 2. MATLAB卡尔曼滤波实践

### 2.1 卡尔曼滤波算法流程

卡尔曼滤波算法是一个递归算法，包括两个主要步骤：预测更新和测量更新。

#### 2.1.1 预测更新

预测更新步骤根据先验信息和上一时刻的状态估计，预测当前时刻的状态和协方差矩阵。其数学表达式如下：

x_pred = A * x_est + B * u;
P_pred = A * P_est * A' + Q;

其中：

* `x_pred`：当前时刻的状态预测值
* `x_est`：上一时刻的状态估计值
* `A`：状态转移矩阵
* `B`：控制输入矩阵
* `u`：控制输入
* `P_pred`：当前时刻的状态协方差矩阵预测值
* `P_est`：上一时刻的状态协方差矩阵估计值
* `Q`：过程噪声协方差矩阵

#### 2.1.2 测量更新

测量更新步骤将当前时刻的测量值与预测值进行融合，更新状态估计和协方差矩阵。其数学表达式如下：

K = P_pred * H' * inv(H * P_pred * H' + R);
x_est = x_pred + K * (z - H * x_pred);
P_est = (eye(size(P_pred)) - K * H) * P_pred;

其中：

* `K`：卡尔曼增益
* `z`：当前时刻的测量值
* `H`：测量矩阵
* `R`：测量噪声协方差矩阵

### 2.2 卡尔曼滤波参数设置

卡尔曼滤波算法的性能受其参数设置的影响，包括过程噪声协方差矩阵、测量噪声协方差矩阵和初始状态估计和协方差矩阵。

#### 2.2.1 过程噪声协方差矩阵

过程噪声协方差矩阵表示系统状态随时间变化的不确定性。其设置方法有：

* **经验法：**根据系统动力学特性和历史数据进行估计。
* **自适应法：**通过在线估计或贝叶斯方法动态调整过程噪声协方差矩阵。

#### 2.2.2 测量噪声协方差矩阵

测量噪声协方差矩阵表示测量值的不确定性。其设置方法有：

* **经验法：**根据测量设备的精度和稳定性进行估计。
* **统计法：**通过测量数据的统计分析得到测量噪声协方差矩阵。

#### 2.2.3 初始状态估计和协方差矩阵

初始状态估计和协方差矩阵表示系统在初始时刻的状态分布。其设置方法有：

* **先验知识：**利用系统模型和先验信息进行估计。
* **历史数据：**利用历史测量数据进行估计。

### 2.3 卡尔曼滤波算法实现

MATLAB中可以使用`kalmanfilter`函数实现卡尔曼滤波算法。其语法如下：

kalmanFilter = kalmanfilter(A, B, H, Q, R, x0, P0);

其中：

* `A`：状态转移矩阵
* `B`：控制输入矩阵
* `H`：测量矩阵
* `Q`：过程噪声协方差矩阵
* `R`：测量噪声协方差矩阵
* `x0`：初始状态估计
* `P0`：初始状态协方差矩阵

使用`kalmanfilter`函数进行卡尔曼滤波的步骤如下：

#### 2.3.1 预测步骤

[x_pred, P_pred] = predict(kalmanFilter);

#### 2.3.2 更新步骤

[x_est, P_est] = correct(kalmanFilter, z);

其中：

* `x_pred`：当前时刻的状态预测值
* `P_pred`：当前时刻的状态协方差矩阵预测值
* `x_est`：当前时刻的状态估计值
* `P_est`：当前时刻的状态协方差矩阵估计值
* `z`：当前时刻的测量值

# 3.1 目标运动模型

目标运动模型描述了目标在空间中的运动规律，是卡尔曼滤波算法中的一个关键因素。不同的目标运动模型适用于不同的目标类型和运动模式。

#### 3.1.1 常量速度模型

常量速度模型假设目标以恒定的速度和方向运动。该模型适用于运动平稳、速度变化不大的目标，例如匀速行驶的车辆或匀速飞行的飞机。

**状态方程：**

x(k+1) = F * x(k) + G * u(k) + w(k)

其中：

* `x(k)`：时刻 `k` 的状态向量，包括位置、速度等信息
* `F`：状态转移矩阵，描述目标运动的线性关系
* `G`：控制输入矩阵，描述控制输入对目标运动的影响
* `u(k)`：时刻 `k` 的控制输入
* `w(k)`：过程噪声，表示目标运动中不可预测的扰动

**观测方程：**

y(k) = H * x(k) + v(k)

其中：

* `y(k)`：时刻 `k` 的观测向量，包括目标的位置或其他可观测信息
* `H`：观测矩阵，描述目标状态与观测值之间的关系
* `v(k)`：测量噪声，表示观测过程中不可避免的误差

#### 3.1.2 加速度模型

加速度模型假设目标以恒定的加速度运动。该模型适用于运动速度变化较大的目标，例如加速行驶的汽车或机动飞行的飞机。

**状态方程：**

x(k+1) = F * x(k) + G * u(k) + w(k)

其中：

* `x(k)`：时刻 `k` 的状态向量，包括位置、速度和加速度
* `F`：状态转移矩阵，描述目标运动的线性关系
* `G`：控制输入矩阵，描述控制输入对目标运动的影响
* `u(k)`：时刻 `k` 的控制输入
* `w(k)`：过程噪声，表示目标运动中不可预测的扰动

**观测方程：**

y(k) = H * x(k) + v(k)

其中：

* `y(k)`：时刻 `k` 的观测向量，包括目标的位置或其他可观测信息
* `H`：观测矩阵，描述目标状态与观测值之间的关系
* `v(k)`：测量噪声，表示观测过程中不可避免的误差

通过选择合适的目标运动模型，卡尔曼滤波算法可以准确地估计目标的状态，并预测其未来的运动轨迹。

# 4. 卡尔曼滤波在传感器融合中的应用

### 4.1 传感器融合概述

#### 4.1.1 传感器类型和特点

传感器融合是将来自多个传感器的信息组合起来，以获得比单个传感器更准确和可靠的信息。传感器类型多种多样，各有特点：

- **惯性传感器：**如加速度计和陀螺仪，测量物体的加速度和角速度。
- **视觉传感器：**如摄像头，获取物体的图像信息。
- **激光雷达：**测量物体到传感器的距离和方向。
- **超声波传感器：**测量物体到传感器的距离。

#### 4.1.2 传感器数据融合方法

传感器数据融合方法主要有：

- **互补滤波：**将来自不同传感器的信息加权平均，权重根据传感器的可靠性确定。
- **卡尔曼滤波：**一种基于贝叶斯概率理论的递归算法，通过预测和更新步骤，不断估计物体的状态。
- **粒子滤波：**一种蒙特卡罗方法，通过模拟粒子群体的运动，估计物体的状态分布。

### 4.2 卡尔曼滤波传感器融合算法

#### 4.2.1 多传感器数据融合

卡尔曼滤波可以用于融合来自多个传感器的同类信息。假设有 `n` 个传感器，每个传感器测量同一物理量 `x`，则卡尔曼滤波算法如下：

**预测步骤：**
x_pred = x_est + u
P_pred = P_est + Q

**更新步骤：**
K = P_pred * H^T * (H * P_pred * H^T + R)^-1
x_est = x_pred + K * (z - H * x_pred)
P_est = (I - K * H) * P_pred

其中：

- `x_est` 为估计状态
- `x_pred` 为预测状态
- `u` 为控制输入
- `P_est` 为估计协方差矩阵
- `P_pred` 为预测协方差矩阵
- `Q` 为过程噪声协方差矩阵
- `H` 为观测矩阵
- `R` 为测量噪声协方差矩阵
- `z` 为测量值

#### 4.2.2 异构传感器数据融合

卡尔曼滤波也可以用于融合来自不同类型传感器的异构信息。例如，可以将来自惯性传感器和视觉传感器的信息融合起来，以估计物体的位姿。异构传感器数据融合算法如下：

**预测步骤：**
x_pred = x_est + u
P_pred = P_est + Q

**更新步骤：**
K = P_pred * H^T * (H * P_pred * H^T + R)^-1
x_est = x_pred + K * (z - H * x_pred)
P_est = (I - K * H) * P_pred

其中：

- `x_est` 为估计状态
- `x_pred` 为预测状态
- `u` 为控制输入
- `P_est` 为估计协方差矩阵
- `P_pred` 为预测协方差矩阵
- `Q` 为过程噪声协方差矩阵
- `H` 为观测矩阵
- `R` 为测量噪声协方差矩阵
- `z` 为测量值

不同之处在于，观测矩阵 `H` 需要根据不同的传感器类型进行修改。

# 5. 卡尔曼滤波在控制系统中的应用

### 5.1 控制系统概述

#### 5.1.1 控制系统类型和结构

控制系统是指通过控制作用器对被控对象进行控制，以实现预期的控制目标的系统。根据被控对象的特性和控制目的，控制系统可以分为以下几种类型：

- **开环控制系统：**控制作用器直接根据输入信号对被控对象进行控制，不考虑被控对象的输出反馈。
- **闭环控制系统：**控制作用器根据输入信号和被控对象的输出反馈进行控制，形成闭环回路。
- **单输入单输出（SISO）控制系统：**只有一个输入信号和一个输出信号。
- **多输入多输出（MIMO）控制系统：**有多个输入信号和多个输出信号。

控制系统的结构通常由以下几个部分组成：

- **传感器：**测量被控对象的输出信号。
- **控制器：**根据传感器测量值和输入信号计算控制作用量。
- **执行器：**将控制作用量施加到被控对象上。
- **被控对象：**接受控制作用量并产生输出信号。

#### 5.1.2 控制系统设计方法

控制系统设计的主要目标是实现预期的控制性能，包括稳定性、精度、响应速度等。常用的控制系统设计方法有：

- **经典控制理论：**基于拉普拉斯变换和传递函数，使用根轨迹法、频率响应法等方法进行设计。
- **现代控制理论：**基于状态空间模型，使用状态反馈控制、最优控制等方法进行设计。
- **自适应控制：**能够根据被控对象的特性和环境变化自动调整控制参数，以保持控制性能。

### 5.2 卡尔曼滤波控制算法

卡尔曼滤波算法可以应用于控制系统中，实现状态估计和控制。

#### 5.2.1 状态反馈控制

状态反馈控制是一种现代控制方法，通过测量被控对象的输出信号和估计其内部状态，计算控制作用量。卡尔曼滤波算法可以用于估计被控对象的状态，为状态反馈控制提供准确的状态信息。

**代码块：**

import numpy as np
import control

# 被控对象模型
A = np.array([[1, 1], [0, 1]])
B = np.array([[0], [1]])
C = np.array([[1, 0]])
D = np.array([[0]])

# 卡尔曼滤波参数
Q = np.eye(2) * 0.001
R = np.eye(1) * 0.01

# 状态反馈控制参数
K = control.lqr(A, B, Q, R)[0]

# 仿真时间
t = np.linspace(0, 10, 100)

# 状态估计和控制
x_hat = np.zeros((2, 1))
u = np.zeros((1, 1))
y = np.zeros((1, 1))

for i in range(len(t)):
    # 状态估计
    x_hat = x_hat + K * (y[i] - C @ x_hat)

    # 控制作用量计算
    u[i] = -K @ x_hat

    # 被控对象输出
    y[i] = C @ x_hat + np.random.normal(0, 0.1)

**逻辑分析：**

代码块实现了状态反馈控制算法，其中卡尔曼滤波用于估计被控对象的状态。

- `A`、`B`、`C`、`D` 为被控对象的系统矩阵。
- `Q`、`R` 为卡尔曼滤波的噪声协方差矩阵。
- `K` 为状态反馈控制的增益矩阵。
- `t` 为仿真时间。
- `x_hat` 为状态估计值。
- `u` 为控制作用量。
- `y` 为被控对象输出。

循环中，首先使用卡尔曼滤波估计状态 `x_hat`，然后根据状态估计值计算控制作用量 `u`，最后将控制作用量施加到被控对象上，得到输出 `y`。

#### 5.2.2 最优控制

最优控制是一种现代控制方法，通过最小化目标函数来计算控制作用量，以实现最佳控制性能。卡尔曼滤波算法可以用于估计被控对象的状态，为最优控制提供准确的状态信息。

**代码块：**

import numpy as np
import scipy.optimize

# 被控对象模型
A = np.array([[1, 1], [0, 1]])
B = np.array([[0], [1]])
C = np.array([[1, 0]])
D = np.array([[0]])

# 卡尔曼滤波参数
Q = np.eye(2) * 0.001
R = np.eye(1) * 0.01

# 最优控制目标函数
def objective(u):
    x_hat = np.zeros((2, 1))
    y = np.zeros((1, 1))

    J = 0
    for i in range(len(t)):
        # 状态估计
        x_hat = x_hat + K * (y[i] - C @ x_hat)

        # 控制作用量计算
        u[i] = -K @ x_hat

        # 被控对象输出
        y[i] = C @ x_hat + np.random.normal(0, 0.1)

        # 目标函数累加
        J += (y[i] - r[i])**2

    return J

# 仿真时间
t = np.linspace(0, 10, 100)

# 参考信号
r = np.sin(t)

# 最优控制求解
u_opt = scipy.optimize.minimize(objective, np.zeros((len(t), 1))).x

**逻辑分析：**

代码块实现了最优控制算法，其中卡尔曼滤波用于估计被控对象的状态。

- `A`、`B`、`C`、`D` 为被控对象的系统矩阵。
- `Q`、`R` 为卡尔曼滤波的噪声协方差矩阵。
- `objective` 函数为最优控制的目标函数。
- `t` 为仿真时间。
- `r` 为参考信号。
- `u_opt` 为最优控制作用量。

`objective` 函数中，使用卡尔曼滤波估计状态 `x_hat`，然后计算控制作用量 `u`，最后计算目标函数值。`scipy.optimize.minimize` 函数用于求解最优控制作用量 `u_opt`。

# 6.1 扩展卡尔曼滤波

### 6.1.1 非线性系统状态方程的线性化

在卡尔曼滤波的标准形式中，系统状态方程和测量方程都是线性的。然而，在实际应用中，许多系统都是非线性的。为了将卡尔曼滤波应用于非线性系统，需要对非线性状态方程进行线性化。

线性化可以通过泰勒展开来实现。设非线性状态方程为：

x(k+1) = f(x(k), u(k))

其中：

* `x(k)` 是状态向量
* `u(k)` 是控制输入
* `f()` 是非线性函数

在 `x(k)` 处的泰勒展开式为：

f(x(k), u(k)) ≈ f(x(k), u(k)) + F(x(k), u(k))(x(k) - x(k))

其中：

* `F(x(k), u(k))` 是雅可比矩阵，其元素为：

F(x(k), u(k)) = ∂f(x(k), u(k))/∂x(k)

* `x(k)` 是 `x(k)` 的估计值

线性化后的状态方程为：

x(k+1) ≈ f(x(k), u(k)) + F(x(k), u(k))(x(k) - x(k))

### 6.1.2 扩展卡尔曼滤波算法

扩展卡尔曼滤波 (EKF) 算法是标准卡尔曼滤波算法的扩展，用于处理非线性系统。EKF 算法的步骤如下：

1. **预测更新**

x(k+1|k) = f(x(k|k), u(k))
P(k+1|k) = F(x(k|k), u(k))P(k|k)F(x(k|k), u(k))' + Q(k)

2. **测量更新**

K(k+1) = P(k+1|k)H(x(k+1|k))'/(H(x(k+1|k))P(k+1|k)H(x(k+1|k))' + R(k))
x(k+1|k+1) = x(k+1|k) + K(k+1)(z(k+1) - h(x(k+1|k)))
P(k+1|k+1) = (I - K(k+1)H(x(k+1|k)))P(k+1|k)

其中：

* `H(x(k+1|k))` 是雅可比矩阵，其元素为：

H(x(k+1|k)) = ∂h(x(k+1|k))/∂x(k+1|k)

* `Q(k)` 是过程噪声协方差矩阵
* `R(k)` 是测量噪声协方差矩阵