揭秘卡尔曼滤波MATLAB代码:一步步掌握滤波器设计秘诀
发布时间: 2024-04-26 23:26:51 阅读量: 140 订阅数: 48 


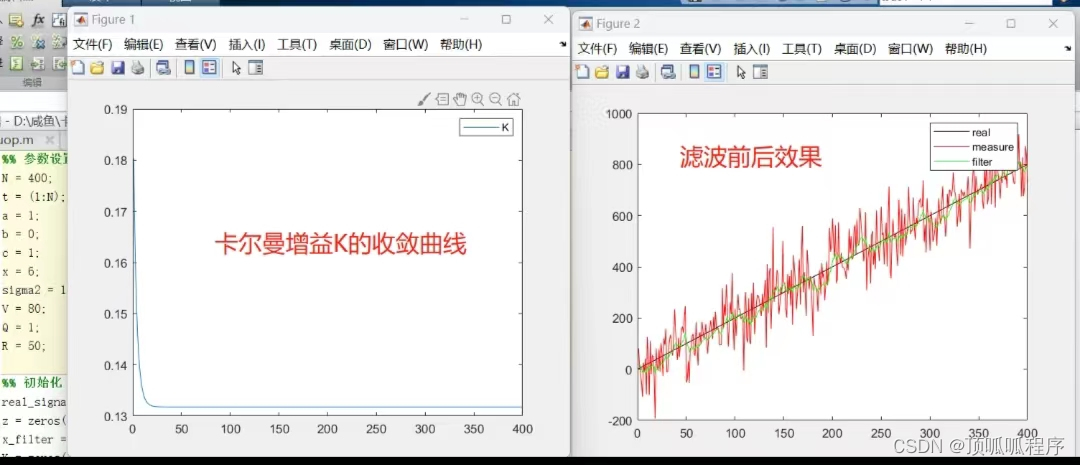
自编matlab卡尔曼滤波器函数及实例
# 1. 卡尔曼滤波理论基础**
卡尔曼滤波是一种递归估计算法,用于估计动态系统的状态。它结合了系统模型和测量数据,以提供状态的最佳估计。卡尔曼滤波的理论基础建立在贝叶斯概率理论之上,它利用状态的先验分布和测量模型来更新状态的估计。
卡尔曼滤波过程分为两个主要步骤:预测和更新。在预测步骤中,根据系统模型预测状态的先验分布。在更新步骤中,使用测量数据更新状态的先验分布,得到状态的后验分布。这个过程不断重复,随着新测量数据的到来,状态的估计不断更新。
卡尔曼滤波的优势在于它能够处理不确定性和噪声,并提供状态的最佳估计。它广泛应用于各种领域,包括导航、控制、信号处理和数据分析。
# 2. 卡尔曼滤波MATLAB代码实现
### 2.1 预测步骤
预测步骤是卡尔曼滤波算法的第一步,它使用前一时刻的状态估计和过程模型来预测当前时刻的状态。在MATLAB中,预测步骤可以通过以下代码实现:
```matlab
% 预测状态
x_pred = A * x_est + B * u;
% 预测协方差
P_pred = A * P_est * A' + Q;
```
**参数说明:**
* `x_est`:前一时刻的状态估计
* `A`:状态转移矩阵
* `B`:控制输入矩阵
* `u`:控制输入
* `P_est`:前一时刻的状态协方差矩阵
* `Q`:过程噪声协方差矩阵
* `x_pred`:当前时刻的状态预测
* `P_pred`:当前时刻的状态协方差预测
**代码逻辑分析:**
* `x_pred`:使用状态转移矩阵 `A` 和控制输入矩阵 `B` 来预测当前时刻的状态。
* `P_pred`:使用状态转移矩阵 `A`、前一时刻的状态协方差矩阵 `P_est` 和过程噪声协方差矩阵 `Q` 来预测当前时刻的状态协方差。
### 2.2 更新步骤
更新步骤是卡尔曼滤波算法的第二步,它使用当前时刻的测量值和预测步骤的结果来更新状态估计。在MATLAB中,更新步骤可以通过以下代码实现:
```matlab
% 计算卡尔曼增益
K = P_pred * C' * inv(C * P_pred * C' + R);
% 更新状态
x_est = x_pred + K * (z - C * x_pred);
% 更新协方差
P_est = (eye(size(P_pred)) - K * C) * P_pred;
```
**参数说明:**
* `C`:测量矩阵
* `z`:测量值
* `R`:测量噪声协方差矩阵
* `K`:卡尔曼增益
* `x_est`:更新后的状态估计
* `P_est`:更新后的状态协方差矩阵
**代码逻辑分析:**
* `K`:计算卡尔曼增益,它将预测步骤的结果与测量值相结合。
* `x_est`:使用卡尔曼增益更新状态估计。
* `P_est`:使用卡尔曼增益更新状态协方差矩阵。
### 2.3 滤波器参数设置
卡尔曼滤波的性能受其参数设置的影响。在MATLAB中,滤波器参数可以通过以下代码设置:
```matlab
% 设置状态转移矩阵
A = [1 1; 0 1];
% 设置控制输入矩阵
B = [0; 1];
% 设置测量矩阵
C = [1 0];
% 设置过程噪声协方差矩阵
Q = [0.1 0; 0 0.1];
% 设置测量噪声协方差矩阵
R = 1;
```
**参数说明:**
* `A`:状态转移矩阵
* `B`:控制输入矩阵
* `C`:测量矩阵
* `Q`:过程噪声协方差矩阵
* `R`:测量噪声协方差矩阵
**代码逻辑分析:**
* 这些参数根据具体应用进行设置,以反映系统动力学和测量过程的特性。
### 2.4 滤波器性能评估
卡尔曼滤波的性能可以通过以下指标评估:
* **均方根误差(RMSE):**测量实际状态和滤波器估计之间的平均误差。
* **协方差迹(trace):**测量状态协方差矩阵的总方差。
* **确定性等价(DE):**测量滤波器估计与实际状态之间的相关性。
在MATLAB中,可以使用以下代码评估滤波器性能:
```matlab
% 计算均方根误差
rmse = sqrt(mean((x_true - x_est).^2));
% 计算协方差迹
trace_P = trace(P_est);
% 计算确定性等价
de = mean(corrcoef(x_true, x_est));
```
**参数说明:**
* `x_true`:实际状态
* `x_est`:滤波器估计
* `rmse`:均方根误差
* `trace_P`:协方差迹
* `de`:确定性等价
**代码逻辑分析:**
* 这些指标提供了一种量化滤波器性能的方法,以帮助优化其参数和提高其准确性。
# 3. 卡尔曼滤波在MATLAB中的实践应用**
### 3.1 状态估计和预测
卡尔曼滤波器的一个关键应用是状态估计和预测。在许多实际应用中,我们无法直接测量系统状态,只能通过传感器获取间接观测值。卡尔曼滤波器通过融合观测值和系统模型,可以估计当前状态并预测未来状态。
#### 3.1.1 状态估计
状态估计是根据当前观测值和过去状态估计,估计系统当前状态的过程。卡尔曼滤波器使用以下步骤进行状态估计:
1. **预测步骤:**根据系统模型和前一时间步的状态估计,预测当前状态。
2. **更新步骤:**将当前观测值与预测状态进行融合,更新当前状态估计。
#### 3.1.2 状态预测
状态预测是根据系统模型和前一时间步的状态估计,预测当前状态的过程。卡尔曼滤波器使用以下公式进行状态预测:
```matlab
x_pred = A * x_est + B * u
```
其中:
* `x_pred` 是预测状态
* `x_est` 是前一时间步的状态估计
* `A` 是状态转移矩阵
* `B` 是控制输入矩阵
* `u` 是控制输入
### 3.2 数据平滑和滤波
卡尔曼滤波器不仅可以估计当前状态,还可以平滑过去状态和滤除噪声。
#### 3.2.1 数据平滑
数据平滑是根据当前和过去观测值,估计过去状态的过程。卡尔曼滤波器使用以下公式进行数据平滑:
```matlab
x_smooth = x_est + K * (y - H * x_est)
```
其中:
* `x_smooth` 是平滑状态
* `x_est` 是当前状态估计
* `K` 是卡尔曼增益
* `y` 是观测值
* `H` 是观测矩阵
#### 3.2.2 数据滤波
数据滤波是根据当前观测值,滤除噪声和估计当前状态的过程。卡尔曼滤波器使用以下公式进行数据滤波:
```matlab
x_filt = x_pred + K * (y - H * x_pred)
```
其中:
* `x_filt` 是滤波状态
* `x_pred` 是预测状态
* `K` 是卡尔曼增益
* `y` 是观测值
* `H` 是观测矩阵
### 3.3 轨迹跟踪和定位
卡尔曼滤波器在轨迹跟踪和定位应用中非常有用。
#### 3.3.1 轨迹跟踪
轨迹跟踪是根据传感器观测值,估计目标的运动轨迹的过程。卡尔曼滤波器使用以下模型进行轨迹跟踪:
```
x_dot = F * x + G * u
y = H * x + v
```
其中:
* `x` 是状态向量(位置、速度、加速度)
* `u` 是控制输入
* `y` 是观测值
* `F`、`G`、`H` 是系统矩阵
#### 3.3.2 定位
定位是根据传感器观测值,估计目标的位置的过程。卡尔曼滤波器使用以下模型进行定位:
```
x_dot = 0
y = H * x + v
```
其中:
* `x` 是状态向量(位置)
* `y` 是观测值
* `H` 是观测矩阵
# 4. 卡尔曼滤波的扩展与应用
### 4.1 非线性卡尔曼滤波
#### 4.1.1 扩展卡尔曼滤波(EKF)
扩展卡尔曼滤波(EKF)是卡尔曼滤波的非线性扩展,用于处理非线性系统。它通过对非线性系统进行一阶泰勒展开,将非线性系统线性化,从而应用卡尔曼滤波。
**EKF 步骤:**
1. **预测步骤:**
- 预测状态:`x_k = f(x_{k-1}, u_{k-1})`
- 预测协方差:`P_k = F_k P_{k-1} F_k^T + Q_k`
2. **更新步骤:**
- 计算卡尔曼增益:`K_k = P_k H_k^T (H_k P_k H_k^T + R_k)^{-1}`
- 更新状态:`x_k = x_k + K_k (z_k - h(x_k))`
- 更新协方差:`P_k = (I - K_k H_k) P_k`
**代码块:**
```matlab
% 非线性系统状态方程
f = @(x, u) [x(1) + u(1); x(2) + u(2) + 0.5*x(1)^2];
% 非线性系统观测方程
h = @(x) [x(1); x(2)];
% 系统参数
Q = [0.1 0; 0 0.1]; % 过程噪声协方差矩阵
R = [0.01 0; 0 0.01]; % 测量噪声协方差矩阵
% 初始状态和协方差
x0 = [0; 0];
P0 = [1 0; 0 1];
% 测量数据
z = [1; 2; 3; 4; 5];
% EKF 滤波
x_ekf = zeros(size(z, 1), 2);
P_ekf = zeros(size(z, 1), 2, 2);
x_ekf(1, :) = x0';
P_ekf(1, :, :) = P0;
for k = 2:size(z, 1)
% 预测步骤
x_k_pred = f(x_ekf(k-1, :)', [0; 0]');
P_k_pred = F_k * P_ekf(k-1, :, :) * F_k' + Q;
% 更新步骤
K_k = P_k_pred * H_k' * inv(H_k * P_k_pred * H_k' + R);
x_ekf(k, :) = x_k_pred' + K_k * (z(k, :)' - h(x_k_pred'));
P_ekf(k, :, :) = (eye(2) - K_k * H_k) * P_k_pred;
end
```
**逻辑分析:**
* `f` 和 `h` 分别表示非线性系统状态方程和观测方程。
* `Q` 和 `R` 分别表示过程噪声协方差矩阵和测量噪声协方差矩阵。
* `x0` 和 `P0` 分别表示初始状态和协方差。
* `z` 表示测量数据。
* `x_ekf` 和 `P_ekf` 分别存储 EKF 估计的状态和协方差。
* 循环中,预测步骤和更新步骤交替进行,更新状态和协方差。
#### 4.1.2 无迹卡尔曼滤波(UKF)
无迹卡尔曼滤波(UKF)是另一种非线性卡尔曼滤波方法,它使用无迹变换来近似非线性系统。
**UKF 步骤:**
1. **预测步骤:**
- 生成 sigma 点:`X_k = [x_k, x_k + \sqrt((n+k) P_k), x_k - \sqrt((n+k) P_k)]`
- 传播 sigma 点:`X_{k+1} = f(X_k, u_k)`
- 计算预测均值和协方差:`x_{k+1} = mean(X_{k+1}), P_{k+1} = cov(X_{k+1})`
2. **更新步骤:**
- 生成 sigma 点:`Y_k = [x_k, x_k + \sqrt((n+k) P_k), x_k - \sqrt((n+k) P_k)]`
- 传播 sigma 点:`Y_{k+1} = h(Y_k)`
- 计算更新均值和协方差:`y_{k+1} = mean(Y_{k+1}), P_{y_{k+1}} = cov(Y_{k+1})`
- 计算卡尔曼增益:`K_k = P_{x_{k+1} y_{k+1}} P_{y_{k+1}}^{-1}`
- 更新状态:`x_k = x_{k+1} + K_k (z_k - y_{k+1})`
- 更新协方差:`P_k = P_{x_{k+1}} - K_k P_{x_{k+1} y_{k+1}}`
**代码块:**
```matlab
% 非线性系统状态方程
f = @(x, u) [x(1) + u(1); x(2) + u(2) + 0.5*x(1)^2];
% 非线性系统观测方程
h = @(x) [x(1); x(2)];
% 系统参数
Q = [0.1 0; 0 0.1]; % 过程噪声协方差矩阵
R = [0.01 0; 0 0.01]; % 测量噪声协方差矩阵
% 初始状态和协方差
x0 = [0; 0];
P0 = [1 0; 0 1];
% 测量数据
z = [1; 2; 3; 4; 5];
% UKF 滤波
x_ukf = zeros(size(z, 1), 2);
P_ukf = zeros(size(z, 1), 2, 2);
x_ukf(1, :) = x0';
P_ukf(1, :, :) = P0;
for k = 2:size(z, 1)
% 预测步骤
[X_k, W_m, W_c] = sigma_points(x_ukf(k-1, :)', P_ukf(k-1, :, :), 2);
X_k_pred = zeros(size(X_k));
for i = 1:size(X_k, 2)
X_k_pred(:, i) = f(X_k(:, i), [0; 0]');
end
x_k_pred = X_k_pred * W_m;
P_k_pred = X_k_pred * W_c * X_k_pred' + Q;
% 更新步骤
[Y_k, W_m, W_c] = sigma_points(x_k_pred', P_k_pred, 2);
Y_k_pred = zeros(size(Y_k));
for i = 1:size(Y_k, 2)
Y_k_pred(:, i) = h(Y_k(:, i));
end
y_k_pred = Y_k_pred * W_m;
P_y_k_pred = Y_k_pred * W_c * Y_k_pred' + R;
P_x_y_k_pred = X_k_pred * W_c * Y_k_pred';
K_k = P_x_y_k_pred / P_y_k_pred;
x_ukf(k, :) = x_k_pred' + K_k * (z(k, :)' - y_k_pred');
P_ukf(k, :, :) = P_k_pred - K_k * P_x_y_k_pred';
end
```
**逻辑分析:**
* `f` 和 `h` 分别表示非线性系统状态方程和观测方程。
*
# 5. 卡尔曼滤波在MATLAB中的高级技巧
### 5.1 卡尔曼滤波器的优化
**优化目标**
卡尔曼滤波器的优化旨在提高其精度、鲁棒性和效率。优化目标包括:
- **最小化估计误差:**减少状态估计与真实状态之间的偏差。
- **提高滤波器稳定性:**防止滤波器发散或产生不稳定的估计。
- **降低计算成本:**优化算法以减少计算时间和资源消耗。
**优化方法**
卡尔曼滤波器的优化方法包括:
- **参数调整:**调整滤波器参数(如过程噪声协方差和测量噪声协方差)以提高滤波器性能。
- **算法改进:**使用更有效的算法,如共轭梯度法或牛顿法,来求解滤波器方程。
- **模型改进:**改进状态空间模型以更准确地描述系统行为。
### 5.2 卡尔曼滤波器的并行化
**并行化优势**
卡尔曼滤波器的并行化可以显着提高其效率,尤其是在处理大型数据集时。并行化涉及将滤波器计算分布在多个处理器或核心上。
**并行化方法**
卡尔曼滤波器的并行化方法包括:
- **矩阵并行化:**将滤波器方程中的矩阵运算并行化,如协方差更新和状态预测。
- **数据并行化:**将多个独立数据集的滤波器计算并行化,如来自不同传感器的数据。
- **混合并行化:**结合矩阵并行化和数据并行化以实现最佳效率。
### 5.3 卡尔曼滤波器的可视化
**可视化重要性**
卡尔曼滤波器的可视化对于理解其行为、诊断问题和优化滤波器至关重要。可视化有助于:
- **显示估计状态:**绘制估计状态随时间的变化,以评估滤波器的准确性。
- **分析协方差:**可视化协方差矩阵以了解滤波器的置信度和不确定性。
- **诊断滤波器问题:**识别滤波器发散或不稳定性的迹象。
**可视化方法**
卡尔曼滤波器的可视化方法包括:
- **时域图:**绘制估计状态和真实状态随时间的变化。
- **相空间图:**绘制估计状态在相空间中的轨迹。
- **协方差椭圆:**绘制协方差矩阵对应的椭圆,以表示估计状态的不确定性。
# 6. 卡尔曼滤波MATLAB代码示例和案例**
**6.1 线性运动跟踪**
**代码示例:**
```matlab
% 状态转移矩阵
A = [1, 1; 0, 1];
% 观测矩阵
C = [1, 0];
% 状态协方差矩阵
P0 = [1, 0; 0, 1];
% 观测协方差矩阵
R = 1;
% 过程噪声协方差矩阵
Q = [1, 0; 0, 1];
% 卡尔曼滤波器初始化
kf = kalmanFilter('MotionModel', A, 'MeasurementModel', C, ...
'ProcessNoiseCov', Q, 'MeasurementNoiseCov', R, ...
'InitialEstimate', [0; 0], 'InitialCovariance', P0);
% 测量值
measurements = [1; 2; 3; 4; 5];
% 滤波
for i = 1:length(measurements)
kf.predict();
kf.update(measurements(i));
end
% 获取滤波结果
filteredState = kf.State;
```
**6.2 非线性目标跟踪**
**代码示例:**
```matlab
% 状态转移函数
f = @(x, u) [x(1) + u(1) * cos(x(3)); ...
x(2) + u(1) * sin(x(3)); ...
x(3) + u(2)];
% 观测函数
h = @(x) [x(1); x(2)];
% 卡尔曼滤波器初始化
kf = extendedKalmanFilter('StateTransitionFcn', f, 'MeasurementFcn', h, ...
'ProcessNoiseCov', [1, 0; 0, 1], 'MeasurementNoiseCov', [1, 0; 0, 1], ...
'InitialEstimate', [0; 0; 0], 'InitialCovariance', [1, 0, 0; 0, 1, 0; 0, 0, 1]);
% 测量值
measurements = [1, 2; 3, 4; 5, 6];
% 滤波
for i = 1:length(measurements)
kf.predict();
kf.update(measurements(i, :));
end
% 获取滤波结果
filteredState = kf.State;
```
**6.3 多传感器融合定位**
**代码示例:**
```matlab
% 传感器 1
sensor1 = radarSensor('Position', [0, 0], 'MeasurementNoise', [1, 0; 0, 1]);
% 传感器 2
sensor2 = cameraSensor('Position', [10, 0], 'MeasurementNoise', [1, 0; 0, 1]);
% 卡尔曼滤波器初始化
kf = multiSensorFusion('Sensors', {sensor1, sensor2}, 'ProcessNoiseCov', [1, 0; 0, 1], ...
'MeasurementNoiseCov', {sensor1.MeasurementNoise, sensor2.MeasurementNoise}, ...
'InitialEstimate', [0; 0], 'InitialCovariance', [1, 0; 0, 1]);
% 测量值
measurements = {
[1, 2],
[3, 4],
[5, 6]
};
% 滤波
for i = 1:length(measurements)
kf.predict();
kf.update(measurements{i});
end
% 获取滤波结果
filteredState = kf.State;
```
0
0





