卡尔曼滤波MATLAB实战案例：解决实际问题，提升技能

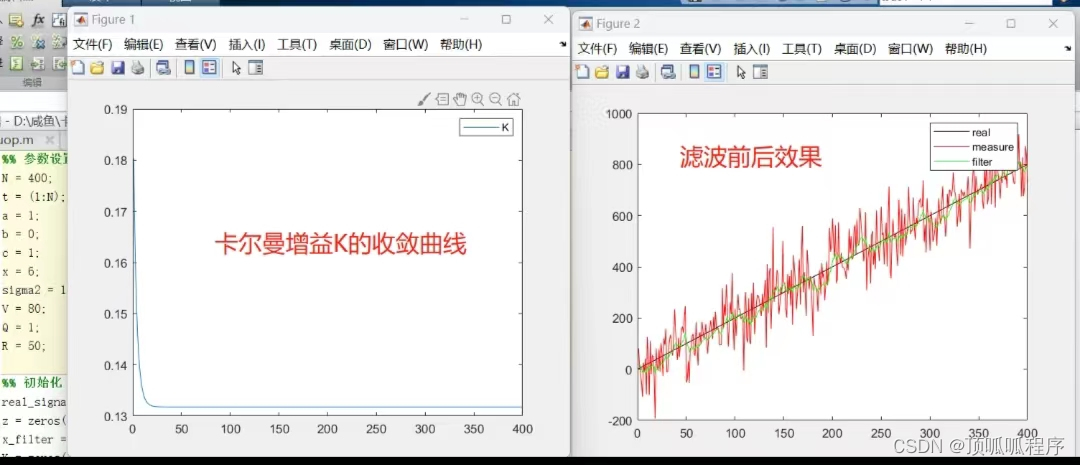
# 1. 卡尔曼滤波理论基础**

卡尔曼滤波是一种递归估计算法，用于估计动态系统的状态。它基于贝叶斯滤波理论，利用系统模型和测量数据来估计系统状态的概率分布。

卡尔曼滤波由两个主要步骤组成：预测和更新。在预测步骤中，滤波器使用系统模型来预测状态的先验分布。在更新步骤中，滤波器使用测量数据来更新状态的后验分布。

卡尔曼滤波的优势在于其能够处理噪声和不确定性。它可以有效地估计非线性系统和非高斯噪声下的状态。

# 2. 卡尔曼滤波 MATLAB 实践

### 2.1 卡尔曼滤波算法的 MATLAB 实现

#### 2.1.1 状态空间模型的建立

卡尔曼滤波算法需要建立状态空间模型来描述系统。状态空间模型由状态方程和观测方程组成：

x(k+1) = A * x(k) + B * u(k) + w(k)
y(k) = C * x(k) + D * u(k) + v(k)

其中：

* `x(k)` 是系统状态向量
* `u(k)` 是系统输入向量
* `y(k)` 是系统输出向量
* `A`、`B`、`C`、`D` 是状态空间模型的系数矩阵
* `w(k)` 和 `v(k)` 是过程噪声和测量噪声，假设它们是均值为 0，协方差分别为 `Q` 和 `R` 的高斯白噪声。

在 MATLAB 中，可以使用 `ss` 函数建立状态空间模型：

A = [1 1; 0 1];
B = [0; 1];
C = [1 0];
D = 0;
sys = ss(A, B, C, D);

#### 2.1.2 滤波器参数的初始化

卡尔曼滤波器需要初始化以下参数：

* **先验状态估计**：`x0`
* **先验状态协方差**：`P0`
* **过程噪声协方差**：`Q`
* **测量噪声协方差**：`R`

这些参数可以通过先验知识或经验估计获得。在 MATLAB 中，可以使用 `kalman` 函数初始化滤波器：

x0 = [0; 0];
P0 = eye(2);
Q = eye(2) * 0.001;
R = eye(1) * 0.01;
kf = kalman(sys, x0, P0, Q, R);

#### 2.1.3 滤波过程的实现

卡尔曼滤波过程包括预测和更新两个步骤：

**预测步骤**：

x_pred(k+1) = A * x_est(k) + B * u(k)
P_pred(k+1) = A * P_est(k) * A' + Q

**更新步骤**：

K(k+1) = P_pred(k+1) * C' * inv(C * P_pred(k+1) * C' + R)
x_est(k+1) = x_pred(k+1) + K(k+1) * (y(k+1) - C * x_pred(k+1))
P_est(k+1) = (eye(size(A)) - K(k+1) * C) * P_pred(k+1)

其中：

* `x_est(k)` 是时刻 `k` 的状态估计
* `P_est(k)` 是时刻 `k` 的状态协方差
* `x_pred(k+1)` 是时刻 `k+1` 的预测状态
* `P_pred(k+1)` 是时刻 `k+1` 的预测状态协方差
* `K(k+1)` 是卡尔曼增益

在 MATLAB 中，可以使用 `predict` 和 `correct` 函数实现滤波过程：

for k = 1:length(y)
    % 预测步骤
    kf = predict(kf);
    % 更新步骤
    kf = correct(kf, y(k));
    % 存储估计状态和协方差
    x_est_history(k, :) = kf.State;
    P_est_history(k, :) = diag(kf.Covariance);
end

# 3. 卡尔曼滤波的工程应用

### 3.1 卡尔曼滤波在导航系统中的应用

卡尔曼滤波在导航系统中扮演着至关重要的角色，它可以有效融合来自不同传感器的数据，提高导航系统的精度和鲁棒性。

#### 3.1.1 惯性导航系统 (INS)

惯性导航系统 (INS) 利用惯性传感器（加速度计和陀螺仪）来测量载体的加速度和角速度，从而推算出其位置、速度和姿态。然而，INS 存在漂移误差，随着时间的推移，其估计值会逐渐偏离真实值。

卡尔曼滤波可以与 INS 结合使用，以补偿漂移误差。卡尔曼滤波器利用 INS 的测量值作为状态预测，并结合来自 GPS 或其他外部传感器的观测值进行更新。通过这种方式，卡尔曼滤波器可以有效地抑制 INS 的漂移误差，提高导航系统的精度。

#### 3.1.2 GPS/INS 集成导航

GPS/INS 集成导航系统将 GPS 和 INS 的优势相结合，实现高精度和连续的导航。GPS 提供绝对位置信息，而 INS 提供高频更新和抗干扰能力。

卡尔曼滤波器在 GPS/INS 集成导航系统中发挥着关键作用。它融合来自 GPS 和 INS 的数据，估计载体的状态（位置、速度、姿态），并补偿 GPS 和 INS 的误差。卡尔曼滤波器可以有效地处理 GPS 信号丢失或干扰的情况，确保导航系统的连续性和可靠性。

### 3.2 卡尔曼滤波在机器人控制中的应用

卡尔曼滤波在机器人控制中有着广泛的应用，它可以帮助机器人准确估计自身状态，并优化控制策略。

#### 3.2.1 状态估计和控制

机器人需要准确估计自身状态（位置、速度、姿态等），才能有效地执行任务。卡尔曼滤波器可以融合来自各种传感器（如激光雷达、IMU、相机）的数据，估计机器人的状态。

基于卡尔曼滤波器估计的状态，机器人可以进行更精确的控制。例如，在移动机器人控制中，卡尔曼滤波器可以估计机器人的位置和速度，并根据估计值调整机器人的运动轨迹。

#### 3.2.2 路径规划和避障

卡尔曼滤波器还可以用于机器人的路径规划和避障。通过估计机器人的状态，卡尔曼滤波器可以预测机器人的未来运动轨迹。基于预测轨迹，机器人可以规划出避开障碍物的路径，并优化其运动策略。

卡尔曼滤波器在机器人控制中的应用极大地提高了机器人的自主性和智能化水平，使其能够执行更复杂的任务。

# 4. 卡尔曼滤波的扩展和优化**

卡尔曼滤波是一种强大的状态估计算法，但它假设系统是线性的，噪声是高斯分布的。在实际应用中，这些假设并不总是成立。为了解决这些限制，卡尔曼滤波的扩展和优化方法应运而生。

## 4.1 扩展卡尔曼滤波 (EKF)

### 4.1.1 非线性系统状态估计

扩展卡尔曼滤波 (EKF) 是卡尔曼滤波的扩展，用于处理非线性系统。它使用一阶泰勒展开来线性化非线性状态方程和观测方程。

**算法步骤：**

1. **预测：**
- 预测状态：`x_k = f(x_{k-1}, u_k)`
- 预测协方差：`P_k = F_k P_{k-1} F_k^T + Q_k`
2. **更新：**
- 计算卡尔曼增益：`K_k = P_k H_k^T (H_k P_k H_k^T + R_k)^{-1}`
- 更新状态：`x_k = x_k + K_k (z_k - h(x_k))`
- 更新协方差：`P_k = (I - K_k H_k) P_k`

其中：

- `x_k`：状态向量
- `u_k`：控制输入
- `f`：非线性状态方程
- `P_k`：协方差矩阵
- `F_k`：状态方程雅可比矩阵
- `Q_k`：过程噪声协方差矩阵
- `z_k`：观测值
- `h`：非线性观测方程
- `H_k`：观测方程雅可比矩阵
- `R_k`：观测噪声协方差矩阵

### 4.1.2 EKF 的 MATLAB 实现

% 定义状态方程和观测方程
f = @(x, u) [x(1) + u; x(2) + x(1)^2];
h = @(x) [x(1); x(2)];

% 初始化状态和协方差
x0 = [0; 0];
P0 = eye(2);

% 过程噪声和观测噪声
Q = diag([0.1, 0.1]);
R = diag([0.01, 0.01]);

% 仿真时间和采样时间
T = 10;
dt = 0.1;

% 存储状态和观测值
x_true = zeros(2, T/dt);
x_est = zeros(2, T/dt);
z = zeros(2, T/dt);

% 仿真
for k = 1:T/dt
    % 真实状态更新
    x_true(:, k) = f(x_true(:, k-1), 0.1);
    % 观测值生成
    z(:, k) = h(x_true(:, k)) + sqrt(R) * randn(2, 1);
    % EKF 预测
    x_k_pred = f(x_est(:, k-1), 0.1);
    P_k_pred = F_k * P_est(:, k-1) * F_k' + Q;
    % EKF 更新
    K_k = P_k_pred * H_k' * inv(H_k * P_k_pred * H_k' + R);
    x_est(:, k) = x_k_pred + K_k * (z(:, k) - h(x_k_pred));
    P_est(:, k) = (eye(2) - K_k * H_k) * P_k_pred;
end

## 4.2 粒子滤波 (PF)

### 4.2.1 非高斯噪声下的状态估计

粒子滤波 (PF) 是一种蒙特卡罗方法，用于处理非高斯噪声下的状态估计。它使用一组称为粒子的随机样本来近似状态分布。

**算法步骤：**

1. **初始化：**
- 生成 `N` 个粒子，并赋予每个粒子一个权重
2. **预测：**
- 根据状态方程，为每个粒子预测状态
3. **更新：**
- 根据观测方程，计算每个粒子的似然函数
- 归一化粒子的权重
4. **重采样：**
- 根据粒子的权重，重新采样粒子，以消除权重退化

### 4.2.2 PF 的 MATLAB 实现

% 定义状态方程和观测方程
f = @(x, u) [x(1) + u; x(2) + x(1)^2];
h = @(x) [x(1); x(2)];

% 初始化粒子
N = 1000;
particles = randn(2, N);
weights = ones(1, N) / N;

% 过程噪声和观测噪声
Q = diag([0.1, 0.1]);
R = diag([0.01, 0.01]);

% 仿真时间和采样时间
T = 10;
dt = 0.1;

% 存储状态和观测值
x_true = zeros(2, T/dt);
x_est = zeros(2, T/dt);
z = zeros(2, T/dt);

% 仿真
for k = 1:T/dt
    % 真实状态更新
    x_true(:, k) = f(x_true(:, k-1), 0.1);
    % 观测值生成
    z(:, k) = h(x_true(:, k)) + sqrt(R) * randn(2, 1);
    % 粒子预测
    particles = f(particles, 0.1) + sqrt(Q) * randn(2, N);
    % 粒子更新
    for i = 1:N
        weights(i) = weights(i) * mvnpdf(z(:, k), h(particles(:, i)), R);
    end
    weights = weights / sum(weights);
    % 粒子重采样
    particles = particles(:, randsample(1:N, N, true, weights));
    weights = ones(1, N) / N;
    % 状态估计
    x_est(:, k) = mean(particles, 2);
end

# 5. 卡尔曼滤波的 MATLAB 工具箱和资源

### 5.1 MATLAB 控制系统工具箱

MATLAB 控制系统工具箱提供了用于设计、分析和仿真控制系统的函数和工具。它包含用于卡尔曼滤波的特定函数，例如：

kalmanfilter: 创建和初始化卡尔曼滤波器
predict: 预测滤波器状态
update: 更新滤波器状态

### 5.2 卡尔曼滤波工具箱

卡尔曼滤波工具箱是一个专门用于卡尔曼滤波的 MATLAB 工具箱。它提供了一系列高级功能，包括：

- 非线性系统状态估计
- 多传感器数据融合
- 鲁棒滤波算法
- 仿真和可视化工具

### 5.3 在线资源和教程

除了 MATLAB 工具箱外，还有许多在线资源和教程可用于学习和使用卡尔曼滤波。一些有用的资源包括：

- [MathWorks 卡尔曼滤波文档](https://www.mathworks.com/help/control/ug/kalman-filter.html)
- [Coursera 卡尔曼滤波课程](https://www.coursera.org/specializations/kalman-filter)
- [Udacity 卡尔曼滤波纳米学位](https://www.udacity.com/school-of-ai/nanodegree/nd031)