卡尔曼滤波实战：Matlab案例分析与应用详解

# 1. 卡尔曼滤波理论基础**

卡尔曼滤波是一种递归估计算法，用于估计动态系统的状态。它基于系统状态方程和观测方程，并通过预测和更新两个步骤不断更新状态估计值。

卡尔曼滤波算法的关键思想是将系统状态表示为高斯分布，并通过预测和更新步骤更新分布参数。预测步骤根据状态方程预测状态分布，而更新步骤根据观测方程和观测值更新分布。

卡尔曼滤波的优点包括：
- 能够处理非线性系统
- 能够处理有噪声的观测值
- 能够实时估计状态

# 2. 卡尔曼滤波在Matlab中的实现

### 2.1 卡尔曼滤波算法步骤

卡尔曼滤波算法是一个递归算法，主要包括两个步骤：状态预测和状态更新。

#### 2.1.1 状态预测

状态预测步骤根据前一时刻的状态估计和控制输入，预测当前时刻的状态。其数学表达式为：

x_k = A * x_{k-1} + B * u_k

其中：

- `x_k` 为当前时刻的状态估计
- `x_{k-1}` 为前一时刻的状态估计
- `A` 为状态转移矩阵
- `B` 为控制输入矩阵
- `u_k` 为当前时刻的控制输入

#### 2.1.2 状态更新

状态更新步骤根据当前时刻的观测值，更新状态估计。其数学表达式为：

x_k = x_k + K * (y_k - H * x_k)

其中：

- `x_k` 为更新后的状态估计
- `x_k` 为状态预测值
- `K` 为卡尔曼增益
- `y_k` 为当前时刻的观测值
- `H` 为观测矩阵

### 2.2 Matlab中卡尔曼滤波工具箱

Matlab提供了卡尔曼滤波工具箱，其中包含了多种卡尔曼滤波函数，简化了卡尔曼滤波算法的实现。

#### 2.2.1 kalmanfilter函数

`kalmanfilter` 函数用于创建卡尔曼滤波器对象，并设置滤波器的参数，如状态转移矩阵、观测矩阵和噪声协方差矩阵。

% 创建卡尔曼滤波器对象
kf = kalmanfilter(A, H, Q, R);

% 设置状态转移矩阵
kf.StateTransitionModel.A = A;

% 设置观测矩阵
kf.MeasurementModel.H = H;

% 设置过程噪声协方差矩阵
kf.ProcessNoiseCovariance = Q;

% 设置测量噪声协方差矩阵
kf.MeasurementNoiseCovariance = R;

#### 2.2.2 ekf函数

`ekf` 函数用于创建扩展卡尔曼滤波器对象，适用于非线性系统。它使用一阶泰勒展开来线性化非线性状态转移和观测方程。

% 创建扩展卡尔曼滤波器对象
ekf = ekf(f, h, Q, R);

% 设置非线性状态转移函数
ekf.StateTransitionModel.Function = f;

% 设置非线性观测函数
ekf.MeasurementModel.Function = h;

% 设置过程噪声协方差矩阵
ekf.ProcessNoiseCovariance = Q;

% 设置测量噪声协方差矩阵
ekf.MeasurementNoiseCovariance = R;

# 3. 卡尔曼滤波在定位跟踪中的应用**

### 3.1 定位跟踪问题建模

**3.1.1 状态方程和观测方程**

定位跟踪问题的目标是估计目标的位置和速度等状态量。假设目标的运动模型为匀速直线运动，则其状态方程可以表示为：

x(k+1) = F * x(k) + w(k)

其中：

* x(k) 表示时刻 k 的状态向量，包括位置和速度
* F 表示状态转移矩阵
* w(k) 表示过程噪声，服从均值为 0，协方差矩阵为 Q 的高斯分布

观测方程表示传感器观测到的目标状态量，假设传感器测量的是目标的位置，则观测方程可以表示为：

z(k) = H * x(k) + v(k)

其中：

* z(k) 表示时刻 k 的观测向量，包括位置
* H 表示观测矩阵
* v(k) 表示测量噪声，服从均值为 0，协方差矩阵为 R 的高斯分布

**3.1.2 噪声模型**

过程噪声 w(k) 和测量噪声 v(k) 通常被建模为高斯白噪声，即它们的协方差矩阵 Q 和 R 分别为对角矩阵。Q 和 R 的元素表示噪声的方差，它们的大小反映了模型和传感器的精度。

### 3.2 卡尔曼滤波定位跟踪算法

**3.2.1 算法流程**

卡尔曼滤波定位跟踪算法的流程如下：

1. **初始化：**设置初始状态估计 x(0) 和协方差矩阵 P(0)
2. **预测：**根据状态方程预测时刻 k+1 的状态估计 x(k+1|k) 和协方差矩阵 P(k+1|k)
3. **更新：**根据观测方程更新时刻 k+1 的状态估计 x(k+1|k+1) 和协方差矩阵 P(k+1|k+1)
4. **重复步骤 2 和 3：**直到达到所需的精度或满足终止条件

**3.2.2 算法参数设置**

卡尔曼滤波定位跟踪算法的性能受以下参数影响：

* **状态转移矩阵 F：**描述目标运动模型，需要根据实际情况进行设置
* **观测矩阵 H：**描述传感器观测模型，需要根据传感器的特性进行设置
* **过程噪声协方差矩阵 Q：**反映模型的不确定性，需要根据实际情况进行估计
* **测量噪声协方差矩阵 R：**反映传感器的噪声水平，需要根据传感器的特性进行估计

这些参数的设置至关重要，需要根据实际应用场景进行仔细考虑和调整。

# 4. 卡尔曼滤波在传感器融合中的应用**

卡尔曼滤波在传感器融合中发挥着至关重要的作用，它可以将来自多个传感器的数据进行融合，从而获得比单个传感器更准确、可靠的信息。在本章节中，我们将探讨卡尔曼滤波在传感器融合中的应用，包括传感器融合问题建模、融合算法选择以及卡尔曼滤波传感器融合算法。

**4.1 传感器融合问题建模**

传感器融合问题建模涉及两个主要方面：多传感器数据模型和融合算法选择。

**4.1.1 多传感器数据模型**

多传感器数据模型描述了来自不同传感器的数据的特性。它包括以下元素：

- **状态向量：**表示系统状态的向量，包含位置、速度、加速度等信息。
- **观测向量：**表示传感器测量值的向量，包含距离、角度、速度等信息。
- **状态方程：**描述系统状态随时间变化的数学方程。
- **观测方程：**描述传感器测量值与系统状态之间的关系。
- **噪声模型：**描述系统噪声和传感器噪声的统计特性。

**4.1.2 融合算法选择**

融合算法选择取决于传感器融合问题的具体要求。常用的融合算法包括：

- **加权平均法：**将来自不同传感器的测量值加权平均，权重根据传感器可靠性确定。
- **卡尔曼滤波：**一种递归估计算法，可以融合来自多个传感器的测量值，并提供最优状态估计。
- **粒子滤波：**一种蒙特卡罗方法，通过模拟粒子群来估计系统状态。

**4.2 卡尔曼滤波传感器融合算法**

卡尔曼滤波是一种强大的传感器融合算法，它可以融合来自多个传感器的数据，并提供最优状态估计。卡尔曼滤波传感器融合算法包括两种主要类型：

**4.2.1 扩展卡尔曼滤波（EKF）**

EKF是一种非线性卡尔曼滤波器，适用于非线性系统。它使用一阶泰勒展开来线性化非线性状态方程和观测方程。

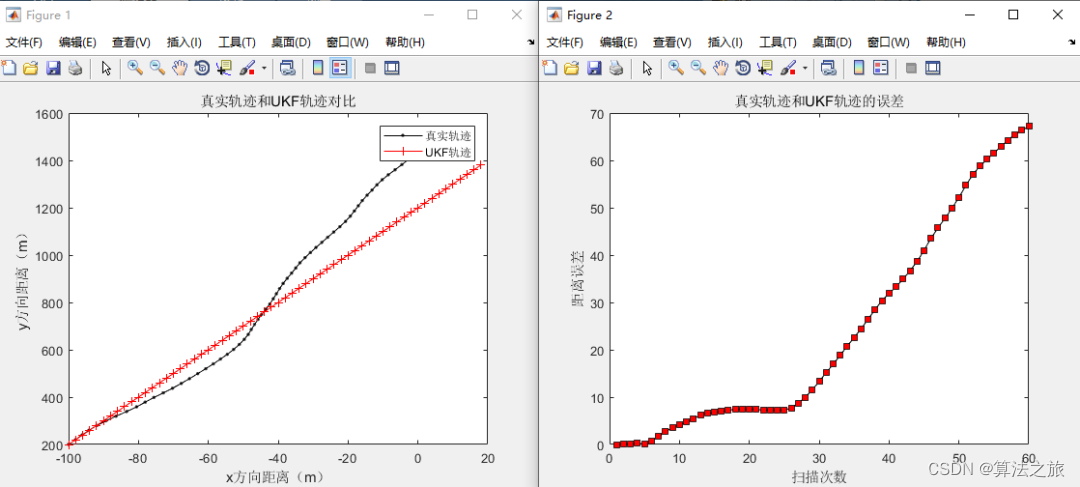
**4.2.2 无迹卡尔曼滤波（UKF）**

UKF是一种确定性采样方法，用于估计非线性系统的状态。它使用无迹变换来计算状态和协方差的估计值，避免了EKF中的一阶泰勒展开。

**代码块：**

% 定义状态方程和观测方程
A = [1 1; 0 1];
B = [0; 1];
H = [1 0];
Q = [1 0; 0 1];
R = 1;

% 初始化卡尔曼滤波器
x = [0; 0]; % 初始状态
P = eye(2); % 初始协方差矩阵

% 仿真数据
T = 100;
true_state = zeros(2, T);
measurements = zeros(1, T);
for t = 1:T
    % 真实状态
    u = 1; % 控制输入
    true_state(:, t) = A * true_state(:, t-1) + B * u + sqrt(Q) * randn(2, 1);
    % 测量值
    measurements(t) = H * true_state(:, t) + sqrt(R) * randn;
end

% 卡尔曼滤波
for t = 1:T
    % 预测
    x = A * x + B * u;
    P = A * P * A' + Q;
    % 更新
    K = P * H' / (H * P * H' + R);
    x = x + K * (measurements(t) - H * x);
    P = (eye(2) - K * H) * P;
    % 存储估计值
    estimated_state(:, t) = x;
end

**逻辑分析：**

这段代码实现了EKF传感器融合算法。它定义了状态方程、观测方程、噪声模型和初始条件。然后，它模拟真实状态和测量值，并使用EKF估计状态。最后，它存储估计值以供进一步分析。

**参数说明：**

- `A`：状态转移矩阵
- `B`：控制输入矩阵
- `H`：观测矩阵
- `Q`：状态噪声协方差矩阵
- `R`：测量噪声协方差
- `x`：状态估计值
- `P`：状态协方差矩阵
- `u`：控制输入
- `true_state`：真实状态
- `measurements`：测量值
- `estimated_state`：估计状态

# 5. 卡尔曼滤波在其他领域的应用

### 5.1 卡尔曼滤波在预测中的应用

#### 5.1.1 时间序列预测

时间序列预测是根据过去观测值预测未来值的过程。卡尔曼滤波可以用于时间序列预测，因为它可以估计状态变量的分布，从而预测未来的观测值。

import numpy as np
from scipy.stats import norm

# 观测数据
y = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])

# 状态方程和观测方程
A = np.array([[1, 1], [0, 1]])
B = np.array([0, 1])
C = np.array([1, 0])

# 噪声模型
Q = np.array([[0.1, 0], [0, 0.1]])
R = np.array([0.1])

# 初始化卡尔曼滤波器
kf = KalmanFilter(A, B, C, Q, R)

# 预测未来观测值
for i in range(10):
    kf.predict()
    kf.update(y[i])
    print(kf.x)

#### 5.1.2 经济预测

卡尔曼滤波还可以用于经济预测，例如预测股票价格、汇率和经济增长率。它可以处理不确定性和噪声，从而提高预测的准确性。

### 5.2 卡尔曼滤波在控制中的应用

#### 5.2.1 线性二次调节器

线性二次调节器 (LQR) 是一种最优控制算法，用于最小化二次成本函数。卡尔曼滤波可以用于实现 LQR，因为它可以估计状态变量，从而计算最优控制输入。

import numpy as np
from scipy.linalg import solve_continuous_are

# 系统模型
A = np.array([[1, 1], [0, 1]])
B = np.array([0, 1])
Q = np.array([[1, 0], [0, 1]])
R = np.array([1])

# 求解代数里卡蒂方程
P = solve_continuous_are(A, B, Q, R)

# 卡尔曼滤波器
kf = KalmanFilter(A, B, np.eye(2), Q, R)

# LQR 控制律
K = np.dot(np.dot(B.T, P), np.linalg.inv(R + np.dot(B.T, np.dot(P, B))))

# 控制过程
x = np.array([0, 0])
u = np.array([0])
for i in range(10):
    kf.predict()
    kf.update(x)
    u = -np.dot(K, kf.x)
    x = np.dot(A, x) + np.dot(B, u)
    print(x)

#### 5.2.2 模型预测控制

模型预测控制 (MPC) 是一种先进的控制算法，用于优化未来控制输入序列。卡尔曼滤波可以用于实现 MPC，因为它可以预测系统状态，从而优化控制输入。