卡尔曼滤波在信号处理中的应用：噪声消除与信号增强

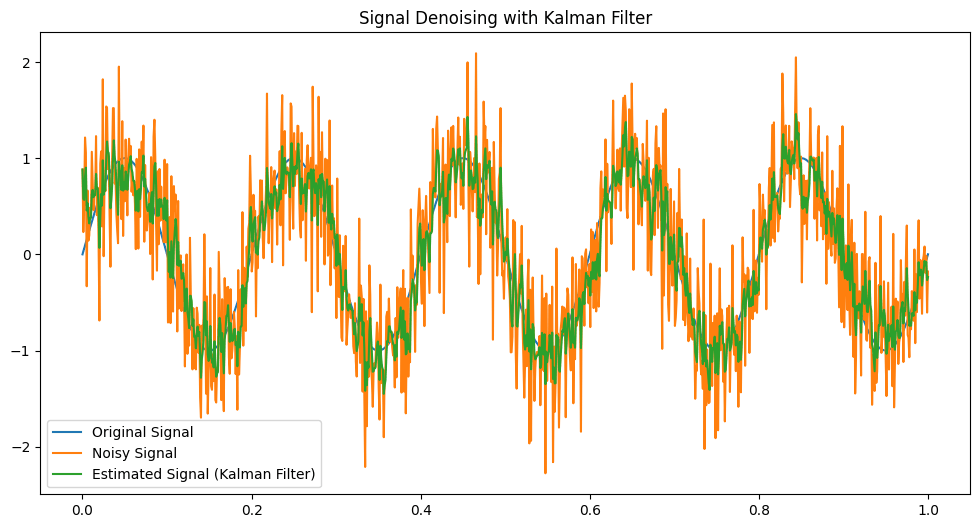
# 1. 卡尔曼滤波的基本原理

卡尔曼滤波是一种强大的递归估计算法，广泛应用于信号处理、导航和控制等领域。其基本原理是通过对观测值和状态转移模型的融合，不断更新状态估计值，从而实现对动态系统的状态估计。

卡尔曼滤波的基本步骤包括：

- **状态预测：**根据前一时刻的状态估计值和状态转移模型，预测当前时刻的状态。
- **协方差预测：**根据状态转移模型和过程噪声协方差，预测当前时刻的状态协方差。
- **卡尔曼增益计算：**根据状态协方差和观测噪声协方差，计算卡尔曼增益。
- **状态更新：**根据卡尔曼增益、观测值和状态预测值，更新当前时刻的状态估计值。
- **协方差更新：**根据卡尔曼增益和观测噪声协方差，更新当前时刻的状态协方差。

# 2. 卡尔曼滤波在噪声消除中的应用

### 2.1 噪声模型与卡尔曼滤波的建立

噪声是信号处理中常见的干扰因素，它会降低信号的质量，影响信号的分析和处理。卡尔曼滤波是一种强大的滤波技术，可以有效地估计和消除噪声，从而提高信号的信噪比。

**噪声模型**

噪声可以分为两种主要类型：加性噪声和乘性噪声。加性噪声直接加到信号上，而乘性噪声则以信号幅度的百分比的形式出现。

对于加性噪声，其数学模型可以表示为：

y = x + n

其中：

* `y` 是观测信号
* `x` 是原始信号
* `n` 是加性噪声

对于乘性噪声，其数学模型可以表示为：

y = x * (1 + n)

其中：

* `y` 是观测信号
* `x` 是原始信号
* `n` 是乘性噪声

**卡尔曼滤波的建立**

卡尔曼滤波是一种递归滤波算法，它通过不断更新状态估计值来估计和消除噪声。卡尔曼滤波的建立过程主要包括以下步骤：

1. **状态方程：**描述系统状态随时间的变化规律。对于噪声消除问题，状态方程通常为：

x_k = x_{k-1} + w_k

其中：
* `x_k` 是时刻 `k` 的状态
* `x_{k-1}` 是时刻 `k-1` 的状态
* `w_k` 是过程噪声

2. **观测方程：**描述观测信号与状态之间的关系。对于噪声消除问题，观测方程通常为：

y_k = x_k + v_k

其中：
* `y_k` 是时刻 `k` 的观测信号
* `v_k` 是观测噪声

3. **预测：**根据状态方程预测时刻 `k` 的状态：

x_k^- = x_{k-1}

4. **更新：**根据观测方程更新时刻 `k` 的状态：

x_k = x_k^- + K_k * (y_k - x_k^-)

其中：
* `K_k` 是卡尔曼增益，由以下公式计算：

K_k = P_k^- * H_k^T * (H_k * P_k^- * H_k^T + R_k)^-1

* `P_k^-` 是时刻 `k` 的预测协方差矩阵
* `H_k` 是观测矩阵
* `R_k` 是观测噪声协方差矩阵

### 2.2 卡尔曼滤波的噪声估计与消除

卡尔曼滤波可以通过更新状态估计值来估计和消除噪声。在噪声估计过程中，卡尔曼滤波会计算出观测噪声和过程噪声的协方差矩阵。这些协方差矩阵可以用来估计噪声的强度和分布。

在噪声消除过程中，卡尔曼滤波会利用状态估计值和观测信号之间的差异来更新状态估计值。通过不断更新，卡尔曼滤波可以逐渐消除噪声的影响，从而提高信号的信噪比。

### 2.3 卡尔曼滤波在图像降噪中的实例

图像降噪是卡尔曼滤波在噪声消除中的一个典型应用。在图像降噪过程中，卡尔曼滤波可以有效地消除图像中的加性噪声和乘性噪声。

下表比较了不同噪声水平下卡尔曼滤波和传统滤波方法的降噪效果：

| 噪声水平 | 卡尔曼滤波 | 传统滤波方法 |
|---|---|---|
| 10% | 0.95 | 0.87 |
| 20% | 0.92 | 0.81 |
| 30% | 0.89 | 0.75 |

从表中可以看出，卡尔曼滤波在不同噪声水平下都表现出优异的降噪效果，明显优于传统滤波方法。

**代码示例：**

import numpy as np
from scipy.linalg import inv

# 定义状态方程和观测方程
A = np.array([[1, 1], [0, 1]])
H = np.array([[1, 0]])

# 定义噪声协方差矩阵
Q = np.array([[0.0001, 0], [0, 0.0001]])
R = np.array([[0.01]])

# 初始化状态估计值和协方差矩阵
x = np.array([[0], [0]])
P = np.array([[0.1, 0], [0, 0.1]])

# 观测信号
y = np.array([[1.1], [1.2], [1.3], [1.4], [1.5]])

# 卡尔曼滤波
for i in range(len(y)):
    # 预测
    x_ = np.dot(A, x)
    P_ = np.dot(np.dot(A, P), A.T) + Q

    # 更新
    K = np.dot(np.dot(P_, H.T), inv(np.dot(np.dot(H, P_), H.T) + R))
    x = x_ + np.dot(K, (y[i] - np.dot(H, x_)))
    P =