卡尔曼滤波在传感器融合中的作用：多传感器数据融合与信息增强

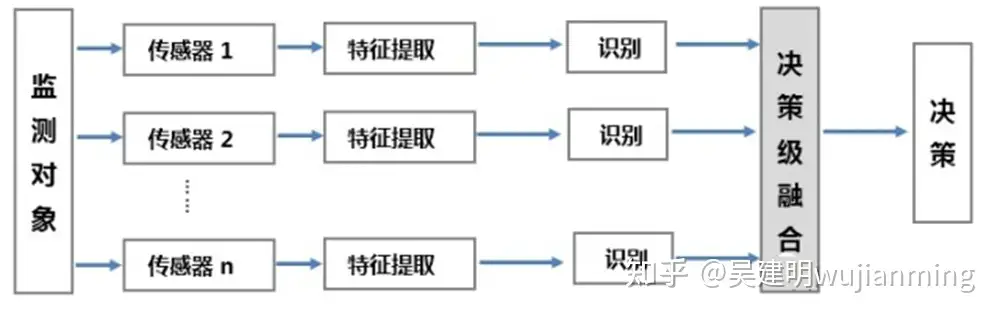
# 1. 卡尔曼滤波的基本原理

卡尔曼滤波是一种递归算法，用于估计动态系统的状态。它基于线性高斯模型，假设系统状态和测量值都是正态分布的。卡尔曼滤波通过两个步骤更新状态估计：预测和更新。

在预测步骤中，滤波器使用系统模型来预测当前状态。预测状态是前一状态的线性变换，加上一个过程噪声项。过程噪声项表示系统状态的不可预测性。

在更新步骤中，滤波器使用测量值来更新预测状态。更新状态是预测状态和测量值的加权平均。权重由卡尔曼增益决定，卡尔曼增益是测量值协方差和预测状态协方差的函数。

# 2. 卡尔曼滤波在传感器融合中的应用

### 2.1 多传感器数据融合的挑战

在实际应用中，单一传感器往往无法满足复杂系统的感知需求。为了提高系统的感知精度和鲁棒性，需要将多个传感器的数据进行融合。然而，多传感器数据融合面临着以下挑战：

- **数据异构性：**不同传感器采集的数据类型、格式和单位可能不同，需要进行数据标准化和转换。
- **数据冗余：**多个传感器可能采集到相同或高度相关的测量数据，导致数据冗余。
- **数据冲突：**不同传感器采集的数据可能存在冲突或不一致，需要进行数据冲突检测和解决。
- **数据延迟：**不同传感器的数据采集和传输时间可能不同，导致数据延迟。
- **数据不确定性：**传感器测量数据通常存在不确定性，需要考虑测量噪声和系统噪声。

### 2.2 卡尔曼滤波的优势和局限性

卡尔曼滤波是一种递归状态估计算法，它能够融合来自多个传感器的测量数据，并估计系统的真实状态。卡尔曼滤波具有以下优势：

- **递归性：**卡尔曼滤波可以基于先前的估计和当前测量数据进行实时状态估计，无需存储所有历史数据。
- **最优性：**在高斯噪声假设下，卡尔曼滤波器能够提供最优的状态估计。
- **鲁棒性：**卡尔曼滤波器能够处理测量噪声和系统噪声，提高状态估计的鲁棒性。

然而，卡尔曼滤波也存在以下局限性：

- **高斯噪声假设：**卡尔曼滤波假设系统噪声和测量噪声服从高斯分布，当实际噪声分布与高斯分布不一致时，卡尔曼滤波的性能会受到影响。
- **线性系统假设：**卡尔曼滤波适用于线性系统，对于非线性系统，需要使用扩展卡尔曼滤波（EKF）或无迹卡尔曼滤波（UKF）等非线性滤波算法。
- **计算复杂度：**卡尔曼滤波的计算复杂度与系统状态维度和传感器数量成正比，对于高维系统或大量传感器，卡尔曼滤波的计算负担可能较大。

### 2.3 卡尔曼滤波在传感器融合中的实现

卡尔曼滤波在传感器融合中的实现步骤如下：

1. **定义系统状态：**确定要估计的系统状态变量，例如位置、速度和加速度。
2. **建立状态方程：**描述系统状态随时间变化的方程，通常为线性方程或非线性方程。
3. **建立观测方程：**描述传感器测量数据与系统状态之间的关系，通常为线性方程或非线性方程。
4. **初始化滤波器：**设置滤波器的初始状态估计和协方差矩阵。
5. **预测：**根据状态方程和先验状态估计，预测当前状态。
6. **更新：**根据观测方程和当前测量数据，更新状态估计。
7. **重复步骤 5 和 6：**不断重复预测和更新步骤，直到达到所需的精度或满足终止条件。

import numpy as np
from scipy.linalg import inv

# 定义系统状态
x = np.array([0, 0])  # 位置和速度

# 定义状态方程
A = np.array([[1, 1], [0, 1]])  # 线性状态方程

# 定义观测方程
H = np.array([[1, 0]])  # 线性观测方程

# 定义系统噪声协方差矩阵
Q = np.array([[0.1, 0], [0, 0.1]])  # 高斯噪声假设

# 定义测量噪声协方差矩阵
R = np.array([0.01])  # 高斯噪声假设

# 初始化滤波器
x_hat = np.array([0, 0])  # 初始状态估计
P = np.array([[1, 0], [0, 1]])  # 初始协方差矩阵

# 测量数据
z = np.array([1])

# 预测
x_hat = A @ x_hat
P = A @ P @ A.T + Q

# 更新
K = P @ H.T @ inv(H @ P @ H.T + R)
x_hat = x_hat + K @ (z - H @ x_hat)
P = (np.eye(2) - K @ H) @ P

**代码逻辑解读：**

- **初始化：**初始化状态估计 `x_hat` 和协方差矩阵 `P`。
- **预测：**根据状态方程 `A` 预测当前状态 `x_hat`，并更新协方差矩阵 `P`。
- **更新：**根据观测方程 `H` 和测量数据 `z` 更新状态估计 `x_hat`，并更新协方差矩阵 `P`。
- **重复：**不断重复预测和更新步骤，直到达到所需的精度或满足终止条件。

# 3.1 惯性导航系统（INS）和全球导航卫星系统（GNSS）融合

#### 惯性导航系统（INS）

惯性导航系统（INS）是一种自主导航系统，它利用惯性传感器（加速度计和陀螺仪）来测量物体的运动。INS 不依赖于外部信号，因此在 GPS 信号不可用或不可靠的情况下非常有用。然而，INS 随着时间的推移会漂移，因此需要定期校正。

#### 全球导航卫星系统（GNSS）

全球导航卫星系统（GNSS）是一种基于卫星的导航系统，它提供位置、速度和时间信息。GNSS 接收器接收来自卫星的信号，并使用这些信号来计算其位置。GNSS 精度高，但容易受到干扰和遮挡。

#### INS 和 GNSS 融合

INS 和 GNSS 融合可以利用这两种系统的优势，同时克服其局限性。INS 提供了高频、短期的运动信息，而 GNSS 提供了低频、长期的位置信息。通过融合这两种数据源，可以获得比单独使用任何一种系统更准确、更可靠的导航解决方案。

**INS 和 GNSS 融合的实现**

INS 和 GNSS 融合可以通过卡尔曼滤波来实现。卡尔曼滤波是一种状态估计算法，它可以将来自不同传感器的数据融合在一起，以获得更准确的状态估计。

在 INS 和 GNSS 融合中，卡尔曼滤波器使用 INS 数据作为状态预测，使用 GNSS 数据作为测量值。卡尔曼滤波器然后更新状态估计，以反映来自两个传感