卡尔曼滤波在预测建模中的应用：时间序列预测与未来趋势分析

# 1. 卡尔曼滤波简介

卡尔曼滤波是一种强大的算法，用于估计动态系统的状态，即使在存在噪声和不确定性的情况下也是如此。它广泛应用于各种领域，包括导航、控制、信号处理和金融。

卡尔曼滤波器由鲁道夫·卡尔曼在 20 世纪 60 年代开发，它是一个递归算法，这意味着它可以根据过去的状态和测量值来更新其估计值。该算法包含两个主要步骤：预测和更新。在预测步骤中，滤波器使用系统模型来预测当前状态。在更新步骤中，滤波器使用测量值来更新预测状态，从而获得更准确的估计值。

# 2. 卡尔曼滤波理论基础

### 2.1 状态空间模型

卡尔曼滤波建立在状态空间模型之上，该模型描述了系统随时间变化的行为。状态空间模型由两个方程组成：状态方程和观测方程。

**状态方程**描述了系统状态如何随时间变化：

x_k = F_k * x_{k-1} + B_k * u_k + w_k

其中：

* `x_k`：时刻 `k` 的系统状态
* `F_k`：状态转移矩阵
* `x_{k-1}`：时刻 `k-1` 的系统状态
* `B_k`：控制输入矩阵
* `u_k`：时刻 `k` 的控制输入
* `w_k`：过程噪声，服从均值为 0，协方差矩阵为 `Q_k` 的高斯分布

**观测方程**描述了如何从系统状态中观察到测量值：

y_k = H_k * x_k + v_k

其中：

* `y_k`：时刻 `k` 的测量值
* `H_k`：观测矩阵
* `v_k`：测量噪声，服从均值为 0，协方差矩阵为 `R_k` 的高斯分布

### 2.2 卡尔曼滤波算法

卡尔曼滤波算法是一个递归算法，用于估计系统状态。该算法分为两个阶段：预测和更新。

**预测阶段**：

* 预测状态：`x_k^- = F_k * x_{k-1}^+ + B_k * u_k`
* 预测协方差：`P_k^- = F_k * P_{k-1}^+ * F_k^T + Q_k`

**更新阶段**：

* 计算卡尔曼增益：`K_k = P_k^- * H_k^T * (H_k * P_k^- * H_k^T + R_k)^-1`
* 更新状态：`x_k^+ = x_k^- + K_k * (y_k - H_k * x_k^-)`
* 更新协方差：`P_k^+ = (I - K_k * H_k) * P_k^-`

其中：

* `x_k^-`：时刻 `k` 的预测状态
* `x_k^+`：时刻 `k` 的更新状态
* `P_k^-`：时刻 `k` 的预测协方差
* `P_k^+`：时刻 `k` 的更新协方差
* `I`：单位矩阵

### 2.3 卡尔曼滤波的收敛性和稳定性

卡尔曼滤波的收敛性和稳定性取决于系统和噪声特性。以下条件有助于确保卡尔曼滤波的收敛性：

* 系统是可控的和可观的。
* 过程噪声和测量噪声是高斯分布的。
* 过程噪声和测量噪声的协方差矩阵是正定的。
* 状态转移矩阵和观测矩阵是稳定的。

如果满足这些条件，卡尔曼滤波将收敛到系统真实状态的无偏估计。

# 3.1 时间序列建模

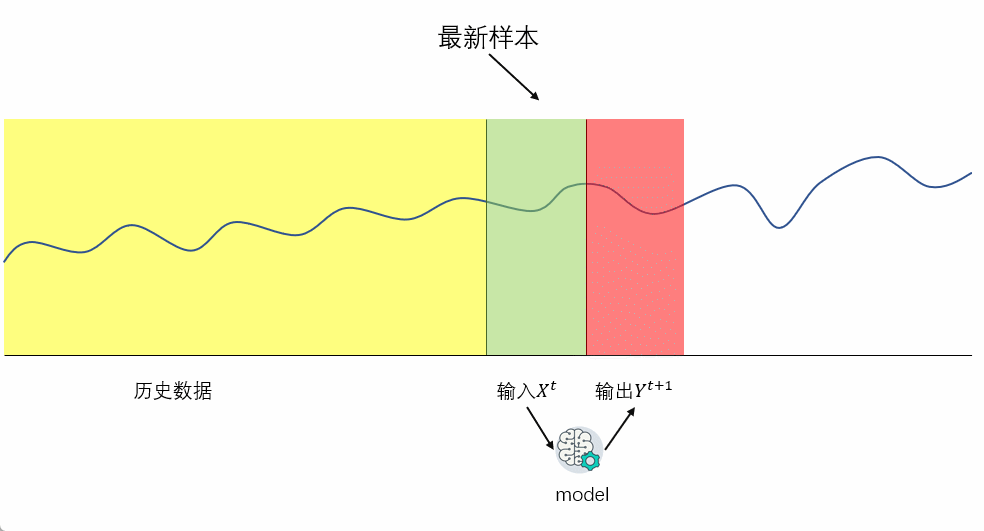
时间序列是一种按时间顺序排列的数据点序列，它描述了某个变量在一段时间内的变化情况。时间序列建模旨在通过数学模型来捕捉时间序列中的模式和趋势，以便进行预测和分析。

在卡尔曼滤波的应用中，时间序列建模是至关重要的，因为它为卡尔曼滤波算法提供了状态空间模型。状态空间模型由两个方程组成：状态方程和观测方程。

**状态方程**描述了系统状态的演化过程，它表示系统在当前时刻的状态如何从前一时刻的状态转移。状态方程通常采用线性形式：

x_t = F * x_{t-1} + B * u_t + w_t

其中：

* `x_t` 是系统在时刻 `t` 的状态向量
* `x_{t-1}` 是系统在时刻 `t-1` 的状态向量
* `F` 是状态转移矩阵
* `B` 是控制输入矩阵
* `u_t` 是控制输入向量
* `w_t` 是过程噪声，它表示系统状态的随机变化

**观测方程**描述了系统状态如何与观测值相关联。观测方程通常也采用线性形式：

y_t = H * x_t + v_t

其中：

* `y_t` 是在时刻 `t` 的观测值
* `x_t` 是系统在时刻 `t` 的状态向量
* `H` 是观测矩阵
* `v_t` 是观测噪声，它表示观测值与系统状态之间的随机误差

### 时间序列建模方法

时间序列建模的方法有很多，常用的方法包括：

* **自回归滑动平均模型 (ARIMA)**：ARIMA 模型是时间序列建模中最常用的方法之一。它使用自回归 (AR) 和滑动平均 (MA) 项来捕捉时间序列中的自相关性。
* **指数平滑法**：指数平滑法是一种简单但有效的时序建模方法。它通过对过去观测值的加权平均来预测未来值。
* **神经网络**：神经网络是一种强大的机器学习模型，可以用于时间序列建模。它们能够捕捉时间序列中的复杂非线性关系。

### 时间序列建模的