卡尔曼滤波在科学研究中的应用：数据分析与建模的强大工具

# 1. 卡尔曼滤波概述

卡尔曼滤波是一种递归估计技术，用于从一组不完全且有噪声的观测值中估计动态系统的状态。它由鲁道夫·卡尔曼于 1960 年提出，自此成为许多工程和科学领域中广泛应用的强大工具。

卡尔曼滤波的基本原理是通过预测和更新两个步骤来逐步估计系统的状态。在预测步骤中，滤波器使用系统状态的先验估计和系统模型来预测当前状态。在更新步骤中，滤波器使用新观测值来更新预测状态，从而获得更准确的估计。

# 2. 卡尔曼滤波理论基础

### 2.1 状态空间模型

状态空间模型是卡尔曼滤波的基础，它描述了系统随时间变化的数学模型。它由两个方程组成：状态方程和观测方程。

#### 2.1.1 状态方程

状态方程描述了系统的内部状态如何随时间变化。它通常表示为：

x_k = A_k * x_{k-1} + B_k * u_k + w_k

其中：

* `x_k` 是系统在时间 `k` 的状态向量
* `A_k` 是状态转移矩阵，描述了状态如何从时间 `k-1` 变化到时间 `k`
* `B_k` 是控制输入矩阵，描述了控制输入 `u_k` 如何影响状态
* `w_k` 是过程噪声，它代表了系统中不可预测的扰动

#### 2.1.2 观测方程

观测方程描述了系统如何被观测到。它通常表示为：

y_k = C_k * x_k + v_k

其中：

* `y_k` 是在时间 `k` 的观测向量
* `C_k` 是观测矩阵，描述了状态如何映射到观测值
* `v_k` 是观测噪声，它代表了观测过程中的不确定性

### 2.2 预测和更新

卡尔曼滤波是一个递归算法，它通过预测和更新步骤不断更新系统的状态估计。

#### 2.2.1 预测步骤

在预测步骤中，卡尔曼滤波根据先前的状态估计和控制输入预测当前状态：

x_k^- = A_k * x_{k-1} + B_k * u_k

其中：

* `x_k^-` 是时间 `k` 的预测状态估计

#### 2.2.2 更新步骤

在更新步骤中，卡尔曼滤波使用当前观测值更新预测状态估计：

x_k = x_k^- + K_k * (y_k - C_k * x_k^-)

其中：

* `x_k` 是时间 `k` 的更新状态估计
* `K_k` 是卡尔曼增益，它确定了观测值对状态估计的影响程度
* `y_k - C_k * x_k^-` 是观测残差，它表示了观测值与预测值之间的差异

# 3.1 数据分析

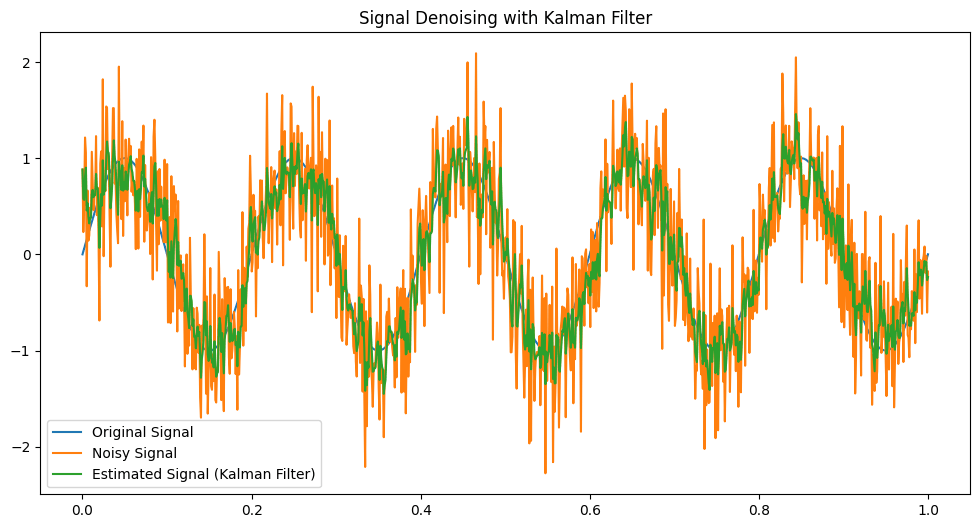
#### 3.1.1 噪声过滤和信号处理

卡尔曼滤波在噪声过滤和信号处理方面有着广泛的应用。它可以从带有噪声的观测值中估计出系统的真实状态，从而提高信号的质量。

**应用场景：**

* **传感器数据处理：**从传感器收集的数据通常会受到噪声和干扰的影响，卡尔曼滤波可以有效地过滤这些噪声，提取出有用的信息。
* **图像处理：**卡尔曼滤波可以用于图像去噪、边缘检测和运动跟踪等任务，提高图像的清晰度和准确性。
* **音频处理：**卡尔曼滤波可以用于音频去噪、语音增强和音乐信号处理，改善音频质量和可理解度。

**代码示例：**

import numpy as np
from scipy.linalg import inv

# 观测数据
y = np.array([1, 2, 3, 4, 5])

#