卡尔曼滤波MATLAB代码在机器人导航中的应用:实现自主移动,解锁无限可能
发布时间: 2024-04-26 23:45:04 阅读量: 102 订阅数: 44 


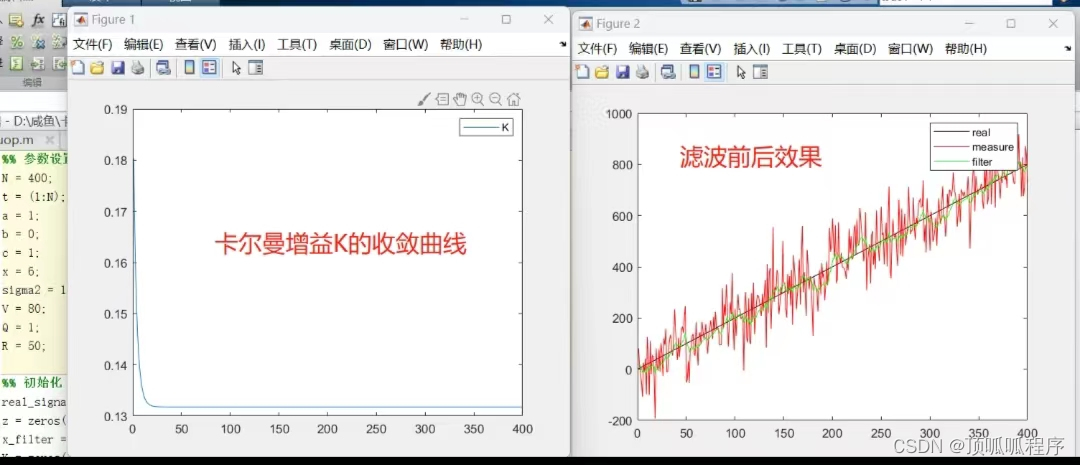
基于MATLAB的卡尔曼滤波机器人定位程序
# 1. 卡尔曼滤波概述**
卡尔曼滤波是一种递归估计算法,用于估计动态系统的状态。它广泛应用于机器人导航、信号处理和控制系统等领域。卡尔曼滤波的主要思想是利用测量值和状态预测值,通过贝叶斯估计来更新状态估计值。
卡尔曼滤波算法由两部分组成:预测和更新。预测步骤基于系统模型和前一时刻的状态估计值,预测当前时刻的状态。更新步骤利用当前时刻的测量值,将预测值与测量值融合,得到新的状态估计值。
卡尔曼滤波算法的优势在于它能够处理噪声和不确定性,并提供最优的状态估计值。它适用于线性系统和非线性系统,并且可以处理多维状态变量。
# 2. 卡尔曼滤波的MATLAB实现
### 2.1 卡尔曼滤波算法原理
卡尔曼滤波是一种递归算法,用于估计动态系统的状态,该系统由以下方程组描述:
```
x_k = A * x_{k-1} + B * u_k + w_k
y_k = C * x_k + v_k
```
其中:
- `x_k` 是系统在时刻 `k` 的状态向量
- `A` 是状态转移矩阵
- `B` 是控制输入矩阵
- `u_k` 是控制输入向量
- `w_k` 是过程噪声向量
- `y_k` 是测量向量
- `C` 是测量矩阵
- `v_k` 是测量噪声向量
卡尔曼滤波算法通过两个步骤来估计状态:预测和更新。
**预测步骤:**
```
x_k^- = A * x_{k-1} + B * u_k
P_k^- = A * P_{k-1} * A^T + Q
```
其中:
- `x_k^-` 是状态的先验估计
- `P_k^-` 是先验协方差矩阵
- `P_{k-1}` 是后验协方差矩阵
- `Q` 是过程噪声协方差矩阵
**更新步骤:**
```
K_k = P_k^- * C^T * (C * P_k^- * C^T + R)^-1
x_k = x_k^- + K_k * (y_k - C * x_k^-)
P_k = (I - K_k * C) * P_k^-
```
其中:
- `K_k` 是卡尔曼增益
- `R` 是测量噪声协方差矩阵
- `I` 是单位矩阵
### 2.2 MATLAB代码实现步骤
#### 2.2.1 状态预测
```matlab
% 状态预测
x_k_minus = A * x_k_1 + B * u_k;
P_k_minus = A * P_k_1 * A' + Q;
```
**代码逻辑分析:**
* `x_k_minus` 是状态的先验估计。
* `P_k_minus` 是先验协方差矩阵。
* `A` 是状态转移矩阵。
* `B` 是控制输入矩阵。
* `u_k` 是控制输入向量。
* `Q` 是过程噪声协方差矩阵。
#### 2.2.2 测量更新
```matlab
% 测量更新
K_k = P_k_minus * C' * inv(C * P_k_minus * C' + R);
x_k = x_k_minus + K_k * (y_k - C * x_k_minus);
P_k = (eye(size(A)) - K_k * C) * P_k_minus;
```
**代码逻辑分析:**
* `K_k` 是卡尔曼增益。
* `x_k` 是状态的后验估计。
* `P_k` 是后验协方差矩阵。
* `C` 是测量矩阵。
* `y_k` 是测量向量。
* `R` 是测量噪声协方差矩阵。
### 2.3 代码优化和性能提升
为了提高卡尔曼滤波算法的性能,可以采用以下优化策略:
- **减少矩阵运算:**使用矩阵运算库(如 NumPy 或 SciPy)可以显着提高矩阵运算的效率。
- **并行化:**如果算法可以并行化,则可以使用多核处理器或 GPU 来提高性能。
- **优化数据结构:**使用高效的数据结构(如稀疏矩阵)可以减少内存使用量并提高计算速度。
- **调整算法参数:**调整卡尔曼滤波算法的参数(如过程噪声和测量噪声协方差)可以提高估计精度。
# 3. 卡尔曼滤波在机器人导航中的应用
### 3.1 机器人导航系统介绍
机器人导航系统是机器人自主移动的基础,其主
0
0





