卡尔曼滤波MATLAB代码在工业控制中的应用：提升系统性能，实现自动化

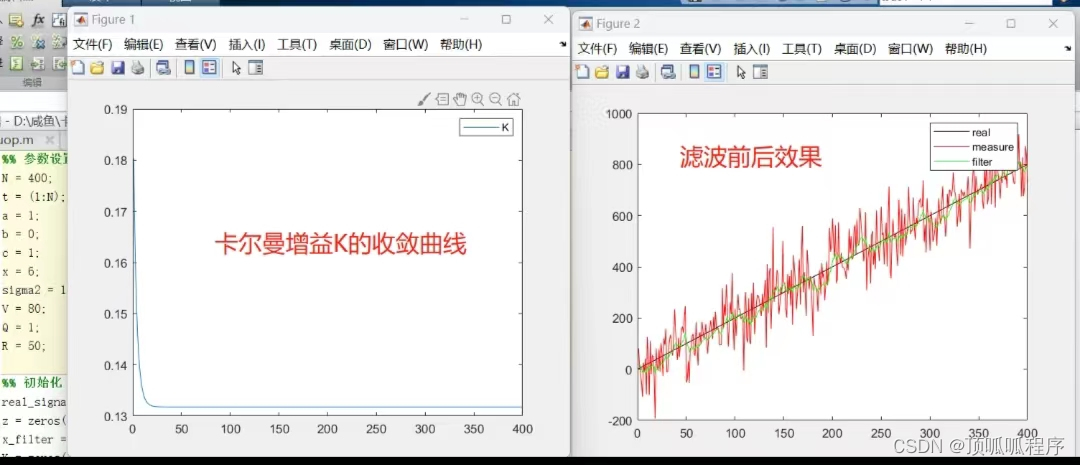
# 1. 卡尔曼滤波理论基础**

卡尔曼滤波是一种递归的估计算法，用于从一系列测量值中估计动态系统的状态。它由鲁道夫·卡尔曼于 1960 年提出，广泛应用于导航、控制和信号处理等领域。

卡尔曼滤波的理论基础建立在状态空间模型之上，该模型将系统描述为状态方程和测量方程。状态方程描述了系统状态随时间的变化，而测量方程描述了测量值与系统状态之间的关系。

# 2. MATLAB卡尔曼滤波编程实践

### 2.1 卡尔曼滤波模型的建立

#### 2.1.1 状态方程和测量方程

卡尔曼滤波模型由两个方程组成：状态方程和测量方程。状态方程描述了系统的动态行为，而测量方程描述了从系统中获取的测量值。

对于线性卡尔曼滤波，状态方程和测量方程可以表示为：

x(k) = A * x(k-1) + B * u(k) + w(k)
y(k) = C * x(k) + v(k)

其中：

* `x(k)` 是系统状态向量
* `u(k)` 是系统控制输入
* `y(k)` 是系统测量输出
* `A`、`B`、`C` 是系统矩阵
* `w(k)` 和 `v(k)` 是过程噪声和测量噪声，它们通常假设为高斯白噪声

#### 2.1.2 噪声协方差矩阵的设定

噪声协方差矩阵描述了过程噪声和测量噪声的统计特性。对于线性卡尔曼滤波，噪声协方差矩阵如下：

Q = E[w(k)w(k)']
R = E[v(k)v(k)']

其中：

* `Q` 是过程噪声协方差矩阵
* `R` 是测量噪声协方差矩阵

噪声协方差矩阵的设定对于卡尔曼滤波的性能至关重要。如果噪声协方差矩阵设置得太小，则滤波器将对噪声过于敏感，导致估计值不稳定。如果噪声协方差矩阵设置得太大，则滤波器将对噪声不敏感，导致估计值滞后。

### 2.2 卡尔曼滤波算法的实现

#### 2.2.1 状态预测

状态预测是卡尔曼滤波算法的第一步。它根据上一时刻的状态估计和控制输入预测当前时刻的状态。状态预测方程如下：

x_pred(k) = A * x_est(k-1) + B * u(k)

其中：

* `x_pred(k)` 是当前时刻的状态预测值
* `x_est(k-1)` 是上一时刻的状态估计值

#### 2.2.2 状态更新

状态更新是卡尔曼滤波算法的第二步。它根据当前时刻的测量值更新状态预测值。状态更新方程如下：

x_est(k) = x_pred(k) + K(k) * (y(k) - C * x_pred(k))

其中：

* `x_est(k)` 是当前时刻的状态估计值
* `K(k)` 是卡尔曼增益
* `y(k)` 是当前时刻的测量值

卡尔曼增益是通过以下公式计算的：

K(k) = P_pred(k) * C' * inv(C * P_pred(k) * C' + R)

其中：

* `P_pred(k)` 是状态预测协方差矩阵

#### 2.2.3 协方差更新

协方差更新是卡尔曼滤波算法的第三步。它根据状态更新值更新状态预测协方差矩阵。协方差更新方程如下：

P_est(k) = (I - K(k) * C) * P_pred(k)

其中：

* `P_est(k)` 是状态估计协方差矩阵
* `I` 是单位矩阵

# 3. 工业控制中的卡尔曼滤波应用

### 3.1 过程控制中的状态估计

#### 3.1.1 系统建模和卡尔曼滤波模型的建立

过程控制中，卡尔曼滤波主要用于状态估计，即根据测量数据估计系统不可直接测量的状态变量。系统建模是卡尔曼滤波应用的关键步骤，需要根据实际系统建立状态方程和测量方程。

**状态方程：**

x(k+1) = Ax(k) + Bu(k) + w(k)

其中：

* x(k) 为时刻 k 的状态向量
* A 为状态转移矩阵
* B 为控制输入矩阵
* u(k) 为时刻 k 的控制输入
* w(k) 为过程噪声，服从均值为 0，协方差矩阵为 Q 的正态分布

**测量方程：**

y(k) = Cx(k) + v(k)

其中：

* y(k) 为时刻 k 的测量值