超参数深度解析：网格搜索vs随机搜索的终极对决

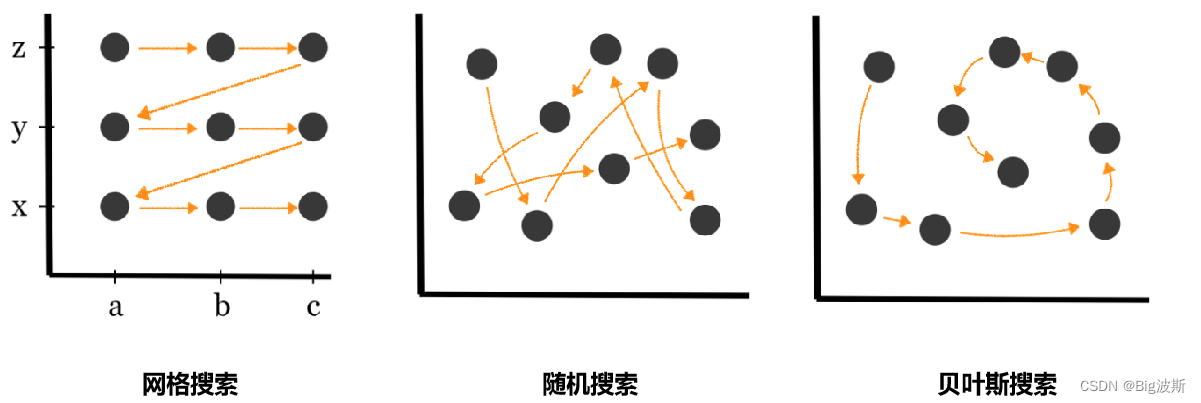
# 1. 超参数优化的理论基础

超参数优化作为机器学习中的一项关键环节，对于模型性能的提升至关重要。超参数是学习算法外部的参数，它们不能通过训练过程直接学习得到，需通过其他手段进行调整和优化。在超参数空间中寻找最优解的过程，涉及到对模型性能的影响评估以及计算资源的有效管理。

为了理解超参数优化的必要性，首先需要明确超参数与模型性能的关系。通常情况下，超参数的选择直接影响模型的泛化能力。例如，学习率、批处理大小、隐藏层神经元数量等超参数的不同设置，会导致模型的训练效率和预测精度有显著差异。

深入研究超参数优化的目标是提升模型在未见数据上的表现，即提高模型的泛化能力。这要求我们在模型的复杂度和过拟合风险之间找到平衡点，通过精心设计的超参数配置来实现。理解这些基础概念，为后续章节中网格搜索和随机搜索等具体方法的介绍奠定了理论基础。

# 2. ```
# 第二章：网格搜索的原理与应用

## 2.1 网格搜索的基本概念

### 2.1.1 超参数与模型性能的关系

超参数是机器学习模型训练前设定的参数，它们不是通过学习过程直接从数据中获得的。模型的性能在很大程度上取决于这些超参数的选择。例如，在支持向量机（SVM）中，正则化参数C和核函数参数gamma对模型的复杂度和泛化能力起着决定性作用。

超参数的选择直接影响到模型的学习过程和最终的性能。不恰当的超参数设置可能导致模型欠拟合或过拟合。欠拟合意味着模型过于简单，无法捕捉数据中的规律；过拟合则意味着模型过于复杂，将训练数据中的噪声也当作了规律。

### 2.1.2 网格搜索的工作原理

网格搜索是一种系统性的超参数优化方法。它通过枚举指定的超参数组合来遍历搜索空间，并使用交叉验证对每种组合进行评估，最终选择出最佳的超参数。

具体来说，网格搜索首先定义一个超参数的范围和步长（例如，步长为0.1），然后生成这个范围内所有可能的超参数组合。对于每个组合，网格搜索使用交叉验证评估其在验证集上的性能，记录下最佳的组合。这个过程可以用如下伪代码表示：

for each hyperparameter combination
    for each fold in cross-validation
        train model with current combination
        evaluate model on validation set
    end for
    compute average performance across folds
end for
select the best hyperparameter combination

## 2.2 网格搜索的实现步骤

### 2.2.1 参数空间的定义

在使用网格搜索之前，需要定义超参数的搜索空间。这通常涉及到两个步骤：确定超参数及其取值范围，以及设置步长。

例如，对于一个决策树模型，可能需要优化的超参数是树的深度（`max_depth`）和最小分割的样本数（`min_samples_split`）。可以定义如下的搜索空间：

param_grid = {
    'max_depth': [None, 2, 4, 6, 8],
    'min_samples_split': [2, 4, 6, 8]
}

### 2.2.2 搜索策略与性能评估

网格搜索通常使用交叉验证来评估超参数组合的性能。最常用的交叉验证方法是k折交叉验证。在k折交叉验证中，数据集被分为k个大小相似的互斥子集。然后，选择一个子集作为验证集，其余的k-1个子集用作训练集。重复这个过程k次，每次选择不同的验证集，最终的性能评估是对k次实验结果的平均。

from sklearn.model_selection import GridSearchCV

# 假设已经准备好模型、数据集等
grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=5, scoring='accuracy')
grid_search.fit(X_train, y_train)

### 2.2.3 网格搜索的优化技巧

尽管网格搜索提供了全面的搜索方法，但它在大规模参数空间中是不切实际的，因为它需要巨大的计算资源和时间。为了提高效率，可以使用如下策略：

1. **随机搜索**：在参数空间中随机选择超参数组合进行尝试。
2. **贝叶斯优化**：根据历史搜索结果，有方向地选择下一个超参数组合。
3. **早停法（Early Stopping）**：当验证集上的性能不再显著提升时停止搜索。

## 2.3 网格搜索的局限性分析

### 2.3.1 维数灾难的问题

随着超参数数量的增加，搜索空间呈指数级增长。这就是所谓的“维数灾难”，它导致了网格搜索需要的计算资源和时间急剧增加。例如，如果有10个超参数，每个超参数有10个可能的值，那么总的组合数将达到10的10次方。

### 2.3.2 计算资源的高消耗

网格搜索的计算成本非常高，特别是在涉及大量的数据和复杂模型时。对于大规模的数据集和高维的特征空间，甚至可能因为计算资源的限制而无法完成搜索。

通过本章节的介绍，我们了解了网格搜索从基本概念到实现步骤，再到优化技巧以及局限性的全面分析。网格搜索是超参数优化中一个重要的工具，尤其适用于参数空间较小且计算资源充足的情况。在下一章节中，我们将探讨网格搜索的替代方案——随机搜索，并比较这两种方法的优缺点。

# 3. 随机搜索的机制与优势

## 3.1 随机搜索的基本理论

### 3.1.1 随机搜索的定义与特点

随机搜索是一种优化算法，它通过随机选择超参数来探索模型配置空间。与网格搜索相比，随机搜索不需要遍历所有可能的参数组合，而是根据预设的概率分布从参数空间中随机抽取点进行评估。这种方法的特点在于简单高效，尤其是当参数空间庞大或连续时。

随机搜索的核心思想是，超参数的某些值可能在模型性能上有显著影响，而其他值则影响较小。因此，随机搜索的重点是发现影响模型性能较大的超参数组合，而不是遍历整个参数空间。

### 3.1.2 随机搜索的数学基础

随机搜索的数学基础可以追溯到统计学和概率论。其背后的数学原理包括随机变量、概率分布以及随机过程。随机搜索通常使用均匀分布或正态分布等来定义参数的采样空间。这种抽样方式允许算法在参数空间中以一定的概率密度进行搜索，从而使得算法可以在有限的尝试次数内更快地找到较好的参数组合。

在理论分析中，随机搜索算法的收敛性受到采样策略的影响。例如，如果采样分布能够很好地覆盖整个参数空间，那么算法更有可能快速收敛到较优解。此外，通过增加采样次数，随机搜索可以提高找到全局最优解的概率。

## 3.2 随机搜索的执行过程

### 3.2.1 参数空间的随机采样

在随机搜索中，参数空间的随机采样是通过定义参数的概率分布来完成的。每个参数都可以有一个独立的分布，或者一组参数可以共享一个联合分布。例如，可以为学习率设定一个对数均匀分布，而对于分类器的正则化项则可能使用高斯分布。

在实际操作中，参数的随机采样可以通过各种编程语言中的随机数生成器来实现。例如，在Python中，可以使用`random`或`numpy`库来生成所需的随机数。

import numpy as np

# 假设有两个超参数，学习率和正则化项
learning_rates = np.logspace(-5, 0, 50) # 对数均匀分布的50个点
regularization_strengths = np.random.normal(0.01, 0.01, 50) # 均值为0.01，标准差为0.01的50个正态分布采样

# 随机组合参数
hyperp