【策略梯度算法深入剖析】：强化学习进阶技巧大揭秘

# 1. 策略梯度算法的理论基础

策略梯度算法是一种在强化学习中被广泛使用的算法，其核心思想是直接对策略进行优化。策略梯度算法通过计算策略的梯度，然后使用梯度上升方法来更新策略，从而使得期望回报最大化。

## 1.1 强化学习与策略梯度

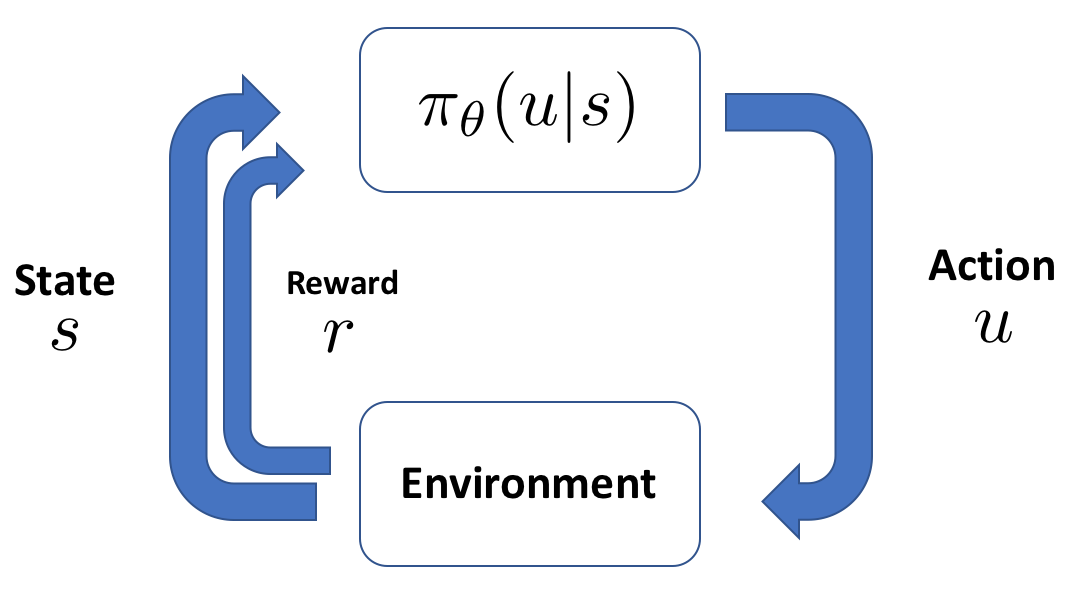
在强化学习中，智能体通过与环境交互，根据观察到的状态采取行动，并从环境中获得奖励。策略梯度算法的核心就是学习一个策略，使得从策略中得到的累积奖励最大化。

为了更好地理解策略梯度算法，我们首先需要理解强化学习的基本元素：状态（State）、动作（Action）、奖励（Reward）和策略（Policy）。策略是一个从状态到动作的映射，描述了在每个状态下应该采取哪种动作。

## 1.2 策略梯度的基本原理

策略梯度算法直接对策略的参数进行优化。考虑到策略参数为θ，我们可以将策略表示为π(θ)，策略梯度的目标就是找到参数θ的最优值，使得长期回报期望最大化。这通过梯度上升方法完成，即每次迭代更新参数θ：

θ = θ + α * ∇θJ(θ)

其中α是学习率，而J(θ)是长期回报的期望值，∇θJ(θ)是策略参数θ的梯度。

## 1.3 策略梯度的关键步骤

策略梯度算法的关键步骤包括：

1. 收集经验：智能体在环境进行探索并收集状态、动作、奖励和下一个状态的数据。
2. 评估策略：根据收集的经验来估计策略梯度。
3. 更新策略：使用估计的梯度更新策略参数，以期改进智能体的表现。
4. 循环迭代：重复以上步骤，直到策略收敛到最优策略。

理解这些理论基础对于深入研究策略梯度算法在实际问题中的应用至关重要。在后续章节中，我们将深入探讨策略梯度算法的具体实现细节和优化技巧。

# 2. 策略梯度算法的实现细节

## 2.1 策略梯度算法的核心概念
### 2.1.1 策略和价值函数

策略梯度算法是一种强化学习方法，通过直接参数化策略并优化目标函数来学习最优策略。这里的策略是指智能体（agent）在特定状态下选择特定动作的概率分布。价值函数，则用于评估特定策略的好坏，包括状态价值函数（state value function）和动作价值函数（action value function）。状态价值函数\(V(s)\)表示从状态s开始，遵循策略\(\pi\)所能获得的期望回报（expected return）。动作价值函数\(Q(s, a)\)表示从状态s采取动作a，之后遵循策略\(\pi\)所能获得的期望回报。策略梯度算法关注于直接优化策略，而不直接优化价值函数。

### 2.1.2 梯度上升和策略更新

策略梯度算法使用梯度上升方法来更新策略参数，以增加策略所获得的总回报。假设策略参数为\(\theta\)，目标函数为\(J(\theta)\)。通过计算目标函数关于策略参数的梯度\(\nabla J(\theta)\)，然后沿梯度的反方向更新参数来增大回报值：

\[
\theta \leftarrow \theta + \alpha \nabla J(\theta)
\]

其中\(\alpha\)是学习率。策略梯度的计算一般涉及到多次采样，即智能体在当前策略下与环境交互，收集轨迹（trajectories），然后基于这些轨迹来估计梯度。REINFORCE算法是策略梯度的一个典型例子，它通过重要性采样来估计梯度。

## 2.2 策略梯度算法的变种
### 2.2.1 REINFORCE算法

REINFORCE算法是一种基于策略梯度的无模型（model-free）算法，它在每次迭代中根据采样轨迹的回报来更新策略。REINFORCE的关键步骤是通过回报的梯度来计算每个动作的选择概率的梯度。更新规则如下：

\[
\nabla J(\theta) \approx \frac{1}{N} \sum_{i=1}^{N} \sum_{t=0}^{T} \nabla_{\theta} \log \pi_{\theta}(a_t^i | s_t^i) R_t^i
\]

其中\(N\)是样本数量，\(T\)是轨迹长度，\(R_t^i\)是从时刻\(t\)开始的回报。

### 2.2.2 Trust Region Policy Optimization (TRPO)

TRPO算法提出了策略更新时需要保持策略变化的“信任区域”的概念。它通过限制策略更新步长来保证更新后的策略不会与原策略有太大偏差，从而保证算法的稳定性和收敛性。TRPO中的目标函数被转化成了一个带约束的优化问题：

\[
\max_\theta \mathbb{E}_{s \sim \rho_{\theta_{old}}, a \sim \pi_{\theta_{old}}(a|s)}\left[\frac{\pi_{\theta}(a|s)}{\pi_{\theta_{old}}(a|s)} A_{\pi_{\theta_{old}}}(s, a)\right]
\]

其中\(A_{\pi_{\theta_{old}}}(s, a)\)是优势函数（advantage function），代表相对于策略\(\pi_{\theta_{old}}\)在(s,a)状态动作对的期望回报。

### 2.2.3 Proximal Policy Optimization (PPO)

PPO是近年来非常流行的策略梯度算法之一，其设计思想是在策略更新时引入一个“截断”或“惩罚”项，用来防止策略更新过于激进。PPO的损失函数被设计为以下形式：

\[
L^{CLIP}(\theta) = \mathbb{E}_t \left[ \min(r_t(\theta) A_t, \text{clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon) A_t) \right]
\]

其中\(r_t(\theta)\)是重要性比率，\(A_t\)是优势函数值，\(\epsilon\)是一个超参数，用来定义截断的范围。

## 2.3 策略梯度算法的性能评估
### 2.3.1 奖励函数设计

在强化学习中，奖励函数的设计对智能体的学习过程至关重要。策略梯度算法依赖于奖励信号来指导学习过程，因此奖励函数的设计需要特别注意。设计奖励函数时，需要考虑如何使奖励与任务目标一致，以及如何避免奖励设计中的常见问题，如稀疏奖励（sparse reward）和延迟奖励（delayed reward）。例如，如果环境不提供足够的立即反馈，则智能体可能很难学习有效的策略。

### 2.3.2 策略稳定性和收敛性分析

策略梯度算法的稳定性与收敛性是衡量算法性能的两个重要指标。稳定性意味着智能体的学习过程不会出现巨大的性能波动，而收敛性则指的是算法能够最终达到一个满意的策略。影响策略梯度算法稳定性和收敛性的因素很多，包括策略表示的形式、学习率选择、梯度估计的方差和偏差等。在实践中，可以利用TRPO和PPO这类算法的变种来提升稳定性，并通过适当的调试学习率和采取一些技巧（如正则化）来减少过拟合，从而增强收敛性。

以上内容详细介绍了策略梯度算法的核心概念、变种实现以及性能评估的重要性。在后续章节中，我们将深入探讨策略梯度算法的优化技巧、实际应用案例以及未来的发展趋势和面临的挑战。

# 3. 策略梯度算法的优化技巧

## 3.1 参数空间和状态空间的优化

### 3.1.1 函数逼近方法

在深度强化学习中，策略梯度算法经常需要处理高维的状态空间和复杂的函数逼近。函数逼近方法是用参数化的函数来近似真实的价值函数或策略函数。常见的逼近方法包括神经网络、决策树和线性模型。

使用神经网络作为函数逼近器，可以学习非线性特征，这对于处理高维数据非常有效。深度神经网络可以捕捉到复杂模式，并通过反向传播算法更新网络权重以最小化损失函数。使用深度学习框架如TensorFlow或PyTorch，可以有效地训练这些网络。

参数空间的优化不仅需要选择合适的函数逼近方法，还需要考虑模型的复杂度。复杂度高的模型可能会导致过拟合，而复杂度低的模型则可能欠拟合。适当的正则化和模型选择对于保证算法在未知环境中的泛化能力至关重要。

### 3.1.2 策略平滑和熵正则化

策略平滑和熵正则化是提高策略梯度算法稳定性的两种常用技术。策略平滑是指在策略更新时加入一定的噪声，使得训练过程更加平滑。这种技术经常用在梯度上升步骤中，可以避免在优化过程中陷入局部最优解。

熵正则化则是一种让策略趋向于随机策略的方法，可以通过向损失函数添加负熵项来实现。增加熵项的目的在于鼓励算法探索更多的状态-动作对，避免过早收敛到非最优策略。熵正则化可以防止策略过早收敛，进而提高算法的探索能力。

在应用这些技术时，需要设置合适的超参数，如噪声的分布、熵正则化系数等。例如，熵正则化系数需要根据具体的任务和环境进行调整，过高会导致策略过于随机，过低则可能无法提供足够的探索。

### 3.1.3 代码块和逻辑分析

以下是一个简单的策略平滑的伪代码示例：

# 伪代码：策略平滑示例
for episode in episodes:
    # 从环境获得初始状态s_0
    s = env.reset()
    done = False
    while not d