PyTorch CNN激活函数全解析：选择与作用揭秘

# 1. 深度学习中的激活函数概述

激活函数在深度学习中扮演着至关重要的角色，它们负责引入非线性特性到神经网络中。非线性特性是区分线性模型与深度学习模型的关键因素，允许网络学习复杂的模式和关系。本章节将从激活函数的定义和分类开始，概述其在深度学习中的基本作用，并介绍为什么激活函数对模型性能至关重要。

## 1.1 激活函数的基本定义

激活函数可以看作是输入信号到输出信号的映射。在神经网络的每一层中，神经元的输入首先被线性加权和偏置，接着通过激活函数进行非线性转换。没有激活函数，无论网络有多少层，最终都只相当于一个单层网络，无法捕捉数据中的非线性关系。

## 1.2 激活函数的分类

激活函数可以大致分为两类：线性激活函数和非线性激活函数。线性激活函数，如线性整流函数（Identity），由于它们不增加额外的非线性，因此较少用于隐藏层。相反，非线性激活函数，如Sigmoid、Tanh和ReLU等，是深度学习中最常用的，因为它们可以提供所需的非线性属性，以便模型能对复杂数据进行建模。

## 1.3 激活函数的重要性

激活函数的重要性不仅在于其引入的非线性，还在于它们对梯度传播和网络训练速度的影响。例如，一些激活函数能够解决梯度消失问题，从而加速网络的训练过程。另外，它们还在不同层之间引入了非线性变换，使网络能够对数据的复杂结构进行建模和学习。在后续章节中，我们将深入探讨各类激活函数在卷积神经网络（CNN）中的具体应用与影响。

激活函数对于深度学习模型的性能至关重要。接下来，我们将进一步探讨在CNN中常用的激活函数及其特点。

# 2. CNN中的常用激活函数

## 2.1 基础激活函数的原理与特点

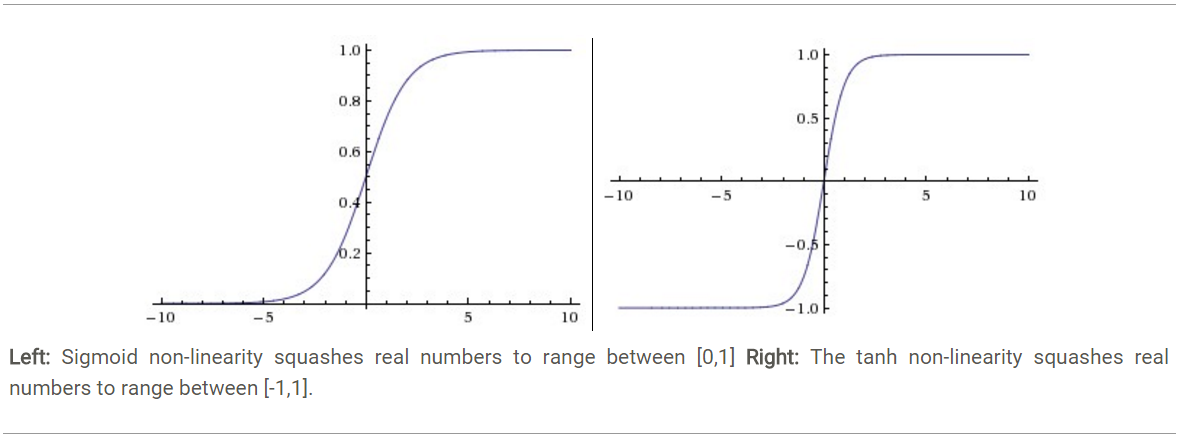
### 2.1.1 Sigmoid函数的数学原理与应用限制

Sigmoid函数（也称为逻辑函数）是一种广泛应用于早期神经网络中的激活函数。其数学表达式为：

\[ \sigma(x) = \frac{1}{1 + e^{-x}} \]

它将输入压缩到0和1之间，输出值可以理解为概率。Sigmoid函数在生物神经元的激励机制上有一定的生物合理性，因为它的输出可以被看作是神经元的激活概率。

然而，Sigmoid函数在现代深度学习中使用得越来越少，主要原因包括：

- **梯度消失问题**：在Sigmoid函数中，当输入值非常大或非常小的时候，其导数趋近于零，导致反向传播时的梯度非常小，使得权重难以更新。
- **计算成本高**：指数运算较昂贵，特别是在神经网络的前向和后向传播过程中，这将导致总体计算开销增加。
- **输出不是零中心化的**：这意味着下一层的输入将倾向于有正的值，这可能导致网络收敛缓慢。

### 2.1.2 Tanh函数的改进与效果分析

双曲正切函数（Tanh）与Sigmoid函数类似，但它输出的范围是-1到1。数学表达式如下：

\[ \tanh(x) = \frac{e^{x} - e^{-x}}{e^{x} + e^{-x}} \]

Tanh函数在一定程度上解决了Sigmoid函数的非零中心化问题，因为它的输出均值接近零，这对于梯度下降法是有利的。然而，Tanh函数仍然面临梯度消失问题，特别是在远离原点的区域。

尽管有这些限制，Tanh函数在某些情况下仍然比ReLU（稍后讨论）表现得更好，特别是在语音生成等序列处理任务中，Tanh能够更好地捕捉数据的非线性。

## 2.2 ReLU及其变体的深入探讨

### 2.2.1 ReLU的优势与常见的变体

ReLU（Rectified Linear Unit）是最常用的激活函数之一。它的函数表达式为：

\[ \text{ReLU}(x) = \max(0, x) \]

ReLU的优势在于其计算简单，并且在很大程度上解决了梯度消失的问题。它在正区间内拥有恒定的梯度（1），使得深层网络中的梯度流动更加顺畅。

然而，ReLU也有其固有的问题：

- **死亡ReLU问题**：在训练过程中，某些神经元可能完全不被激活，这意味着它们永远不会对损失函数产生影响，从而导致这些神经元“死亡”。
- **负值区域导数为零**：ReLU在负区间内导数为零，这导致了权重无法更新。

为了克服这些问题，研究人员提出了一些ReLU的变体，比如Leaky ReLU和Parametric ReLU（PReLU）。Leaky ReLU通过为负区间赋予一个很小的斜率（例如0.01），以保证导数不为零；而PReLU将这个斜率作为一个学习参数，使得网络能够自动学习到最佳的斜率值。

### 2.2.2 ReLU变体的性能对比与选择

ReLU及其变体的性能对比，通常需要基于具体任务和数据集进行。在大多数情况下，ReLU或其变体都显示出了优越性，特别是在深度网络中。然而，由于ReLU变体的存在，选择哪一个并没有统一的答案。

实验表明，PReLU通常比Leaky ReLU和标准ReLU表现得更好，因为它赋予了网络更多的灵活性来适应数据。然而，在实际应用中，Leaky ReLU因其简单性而被广泛采用。

在选择激活函数时，还应该考虑网络的深度、问题的复杂性、计算资源等因素。例如，对于相对浅层的网络，Tanh可能是一个不错的选择；而对于深层网络，ReLU及其变体通常更加适合。

## 2.3 高级激活函数简介

### 2.3.1 Swish和Mish等新激活函数的提出背景

近年来，随着研究的深入，研究人员提出了新的激活函数，如Swish和Mish。Swish由Google提出，其表达式为：

\[ \text{Swish}(x) = x \cdot \sigma(x) \]

Swish函数旨在提供一种能够平滑地替换ReLU的激活函数，以期获得更好的性能。实验表明，Swish在某些深度学习任务中能够达到与ReLU相媲美甚至更好的性能。

Mish是另一个新出现的激活函数，其表达式为：

\[ \text{Mish}(x) = x \cdot \tanh(\text{Swish}(x)) \]

Mish函数具有平滑的非单调性质，它被证明在多种任务中都显示出优越性，比如图像识别和自然语言处理。

### 2.3.2 新激活函数的实验结果与实际应用价值

新激活函数的提出往往伴随着一系列实验来验证其有效性。这些实验通常在标准的基准数据集（如ImageNet）上进行，并通过比较不同激活函数下的准确率、损失函数的收敛速度等指标来评估效果。

尽管Swish和Mish等新激活函数显示出良好的实验结果，但它们并没有完全取代ReLU及其变体。原因在于新激活函数可能会引入更多的计算负担，并且对于特定任务来说，这种优势可能并不明显。此外，现有的大多数深度学习库和框架已经高度优化了ReLU的实现，使得在不显著提高性能的情况下更换激活函数可能并不是最优选择。

在实际应用中，新激活函数的使用应该基于具体的项目需求和性能测试。例如，如果一个特定的激活函数在特定的网络架构上显著提高了性能，那么它可能是值得考虑的。然而，由于ReLU及其变体的广泛应用和相对简单性，它们仍然是大多数场景下默认的选择。

在本章节的介绍中，我们详细探讨了CNN中常用的几种激活函数及其变体，并对比了它们的原理、优缺点以及在实践中的应用情况。在下一章节中，我们将深入了解激活函数如何在CNN中发挥其作用，并分析其对网络性能的具体影响。

# 3. 激活函数在CNN中的作用

在第三章中，我们将深入了解激活函数在卷积神经网络（CNN）中的具体作用，探讨它们如何影响网络性能，并提供实际应用案例分析。

## 3.1 激活函数对CNN性能的影响

### 3.1.1 激活函数在前向传播中的角色

激活函数在CNN的前向传播过程中扮演着至关重要的角色。它们引入了非线性，使得CNN能够捕捉和学习到输入数据的复杂特征。如果没有激活函数，无论网络有多少层，最终的输出都只是输入数据的线性组合，这样的模型将无法解决实际问题中的非线性问题。Sigmoid和Tanh等早期激活函数在前向传播中能够提供平滑的非线性变换，而ReLU及其变体则通过限制负值的梯度来提高网络的训练速度。

### 3.1.2 激活函数如何影响梯度和网络训练

激活函数的选择直接影响梯度的传播方式和网络的训练效率。对于Sigmoid和Tanh这样的饱和激活函数，当输入值远离0时，梯度几乎为0，这会导致梯度消失问题，使得深层网络难以训练。而ReLU函数则通过简单的阈值机制，解决了梯度消失的问题，加快了训练速度。然而，ReLU在负值区域的梯度为零，可能会导致“死亡ReLU”问题，即部分神经元在训练过程中永久不活跃。为了解决这个问题，研究者们提出了ReLU的变体，如Leaky ReLU和Parametric ReLU，以保持负值区域的小梯度，从而使得激活函数更加鲁棒。

## 3.2 激活函数在模型优化中的作用

### 3.2.1 激活函数的选择对模型泛化能力的影响

模型的泛化能力是指模型对未知数据的预测能力。激活函数的选择对模型的泛化能力有着直接的影响。例如，使用ReLU激活函数的网络倾向于获得稀疏激活，这有助于减少模型的复杂度，并可能提高模型的泛化能力。然而，过度稀疏也可能导致过拟合，特别是当网络过大或训练数据不足时。因此，选择合适的激活函数需要平衡模型的复杂性和训练数据的数量。

### 3.2.2 激活函数在模型压缩和加速中的应用

随着深度学习模型变得越来越复杂，模型压缩和加速成为了实际应用中不可忽视的问题。激活函数的特性被用于模型压缩技术中，例如，在二值化或量化网络中，通过选择合适的激活函数，可以减少模型参数的数量，从而减少计算资源的使用。此外，使用如Swish这样的激活函数，它可以提供比ReLU更好的性能，同时保持了相对较低的计算复杂度。

## 3.3 激活函数在特定任务中的应用案例

### 3.3.1 图像分类任务中的激活函数应用