PID调节器抗干扰性提升秘籍：应对干扰，保障系统稳定

# 1. PID调节器基础理论**

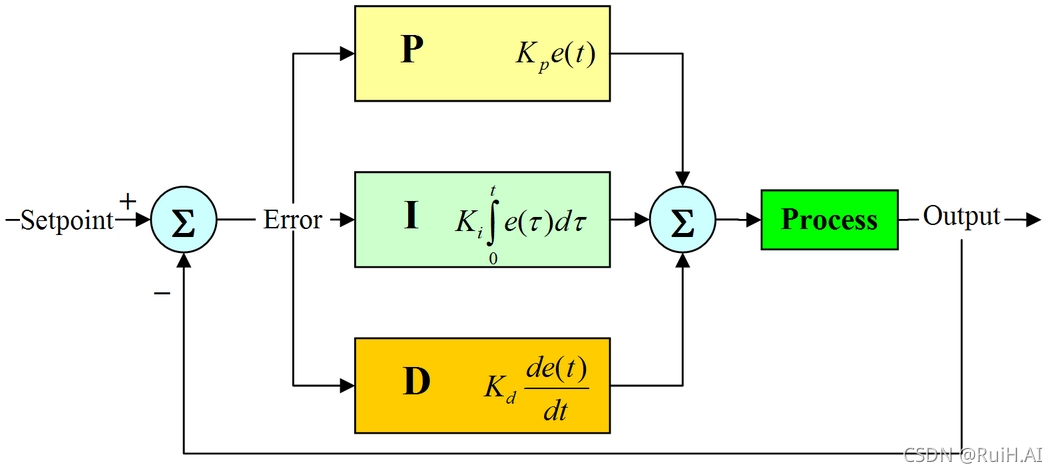
PID（比例-积分-微分）调节器是一种广泛应用于工业过程控制中的反馈控制器。它通过测量系统输出与设定值之间的偏差，并根据偏差的比例、积分和微分值调整控制输出，从而实现对系统输出的稳定控制。

PID调节器的基本结构如图所示：

graph LR
subgraph PID调节器
    A[设定值] --> |比例| --> B[偏差]
    B --> |积分| --> C[积分项]
    B --> |微分| --> D[微分项]
    C --> E[控制输出]
    D --> E
end

其中，偏差为设定值与系统输出之差。比例项根据偏差的大小调整控制输出，积分项消除偏差的累积效应，微分项预测偏差的变化趋势，从而提高系统的响应速度和稳定性。

# 2. 干扰分析与抗干扰策略

### 2.1 干扰分类与影响

#### 2.1.1 过程干扰

过程干扰是指作用于被控对象过程本身的干扰，包括：

- **负载干扰：**外部负载变化引起的干扰，如机械负载、流量变化等。
- **参数干扰：**被控对象参数变化引起的干扰，如温度变化、摩擦系数变化等。
- **环境干扰：**外部环境变化引起的干扰，如温度、湿度、风速等。

#### 2.1.2 测量干扰

测量干扰是指作用于测量环节的干扰，包括：

- **传感器噪声：**传感器本身产生的随机噪声。
- **量程限制：**传感器量程限制引起的非线性干扰。
- **环境影响：**外部环境因素对测量信号的影响，如电磁干扰、振动等。

### 2.2 抗干扰策略概述

抗干扰策略是指通过各种手段减轻干扰对PID调节器控制效果的影响，主要分为以下几类：

#### 2.2.1 滤波技术

滤波技术通过对测量信号进行处理，滤除干扰信号，从而提高测量信号的信噪比。常用的滤波技术包括：

- **平滑滤波器：**通过对测量信号进行平均或加权平均，去除高频噪声。
- **卡尔曼滤波器：**一种状态空间滤波器，可以同时估计系统状态和测量噪声。

#### 2.2.2 预测补偿

预测补偿通过预测未来干扰信号，并提前采取控制措施，从而抵消干扰的影响。常用的预测补偿技术包括：

- **模型预测控制（MPC）：**基于系统模型，预测未来控制输出，并优化控制策略，以最小化干扰影响。
- **神经网络预测：**利用神经网络学习干扰信号的规律，并进行预测。

#### 2.2.3 鲁棒控制

鲁棒控制通过设计控制器，使系统对干扰具有鲁棒性，即系统在一定范围内干扰变化时，仍能保持稳定和性能。常用的鲁棒控制技术包括：

- **滑模控制：**通过设计滑模面，使系统状态在滑模面上滑动，从而对干扰具有鲁棒性。
- **H∞控制：**一种基于H∞范数的鲁棒控制方法，可以保证系统在最坏情况下具有鲁棒稳定性。

# 3. PID调节器抗干扰实践**

**3.1 滤波抗干扰**

滤波技术是一种常用的抗干扰策略，通过滤除干扰信号中的高频分量，从而降低其对系统的影响。常用的滤波器包括：

**3.1.1 平滑滤波器**

平滑滤波器是一种简单的滤波器，通过对输入信号进行平均，从而消除高频干扰。其原理如下：

def smooth_filter(data, window_size):
    """平滑滤波器

    Args:
        data: 输入信号
        window_size: 平滑窗口大小

    Returns:
        滤波后的信号
    """
    filtered_data = []
    for i in range(len(data)):
        start = max(0, i - window_size + 1)
        end = i + 1
        filtered_data.append(np.mean(data[start:end]))
    return filtered_data

**逻辑分析：**

`smooth_filter` 函数通过一个滑动窗口对输入信号进行平均，窗口大小由 `window_size` 参数指定。对于每个窗口，函数计算窗口内数据的平均值，并将其作为滤波后的输出。

**3.1.2 卡尔曼滤波器**

卡尔曼滤波器是一种递归滤波器，它结合了状态空间模型和测量数据，从而估计系统状态和滤除干扰。其原理如下：

import numpy as np
from scipy.linalg import inv

def kalman_filter(A, B, C, Q, R, x0, P0, y):
    """卡尔曼滤波器

    Args:
        A: 状态转移矩阵
        B: 输入矩阵
        C: 输出矩阵
        Q: 状态噪声协方差矩阵
        R: 测量噪声协方