PID调节器精准把控温度：温度控制中的应用实践

# 1. PID调节器理论基础**

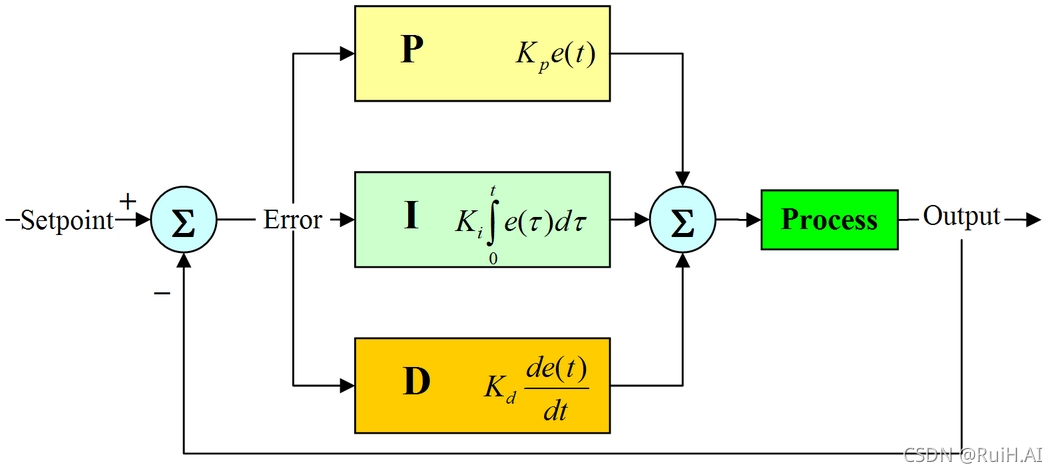
PID调节器（Proportional-Integral-Derivative Controller）是一种反馈控制系统，广泛应用于温度控制等领域。其基本原理是：根据被控对象的偏差（误差）来调整控制输出，从而实现对被控对象的精准控制。

PID调节器由三个基本组成部分组成：比例（P）项、积分（I）项和微分（D）项。P项根据偏差的当前值进行调整，I项根据偏差的累积值进行调整，D项根据偏差变化率进行调整。通过调整这三个参数的比例，可以实现对被控对象的快速响应、平稳控制和抗干扰能力的优化。

# 2. PID调节器实践应用

### 2.1 PID参数的选取和优化

PID调节器的性能很大程度上取决于其参数的选取和优化。有几种方法可以确定合适的PID参数，包括：

#### 2.1.1 Ziegler-Nichols方法

Ziegler-Nichols方法是一种经典且广泛使用的PID参数选取方法。该方法基于阶跃响应的分析，步骤如下：

1. 将PID控制器切换到P控制模式，并将P增益逐渐增加，直到系统出现持续振荡。
2. 记录振荡的周期（T）和振幅（A）。
3. 根据T和A，使用下表确定PID参数：

| 控制器类型 | Kp | Ti | Td |
|---|---|---|---|
| P | 0.5 * Kc | - | - |
| PI | 0.45 * Kc | 0.85 * T | - |
| PID | 0.6 * Kc | 0.5 * T | 0.125 * T |

其中，Kc = 1.2 / A。

**代码块：**

import numpy as np

def ziegler_nichols(T, A):
  """
  Ziegler-Nichols方法计算PID参数。

  参数：
    T: 振荡周期
    A: 振荡幅度

  返回：
    Kp, Ti, Td: PID参数
  """

  Kc = 1.2 / A
  Kp = 0.5 * Kc
  Ti = 0.85 * T
  Td = 0.125 * T

  return Kp, Ti, Td

**逻辑分析：**

该代码块实现了Ziegler-Nichols方法。它接收振荡周期（T）和振幅（A）作为输入，并根据这些值计算PID参数（Kp、Ti、Td）。

#### 2.1.2 试差法

试差法是一种迭代方法，通过逐步调整PID参数来优化系统性能。步骤如下：

1. 将PID控制器切换到P控制模式，并设置一个初始P增益。
2. 观察系统的响应，并根据误差调整P增益。
3. 添加I控制，并调整Ti以减少误差的积分。
4. 添加D控制，并调整Td以减少误差的导数。

**代码块：**

import time

def trial_and_error(pid, error_threshold):
  """
  试差法优化PID参数。

  参数：
    pid: PID控制器对象
    error_threshold: 误差阈值

  返回：
    Kp, Ti, Td: 优化后的PID参数
  """

  Kp = 0.1
  Ti = 1.0
  Td = 0.1

  while True:
    pid.set_parameters(Kp, Ti, Td)
    error = pid.get_error()

    if abs(error) < error_threshold:
      break

    # 调整参数
    if error > 0:
      Kp += 0.01
    else:
      Kp -= 0.01

    if error > 0:
      Ti += 0.1
    else:
      Ti -= 0.1

    if error > 0:
      Td += 0.01
    else:
      Td -= 0.01

  return Kp, Ti, Td

**逻辑分析：**

该代码块实现了试差法。它接收一个PID控制器对象（pid）和一个误差阈值（error_threshold）作为输入。它迭代地调整PID参数（Kp、Ti、Td），直到误差低于阈值。

# 3.1 温度传感器的选择和安装

**温度传感器的选择**

温度传感器的选择至关重要，因为它直接影响温度控制系统的