【PID调节器实战指南】：从原理到应用，一文掌握PID控制

# 1. PID调节器基础理论**

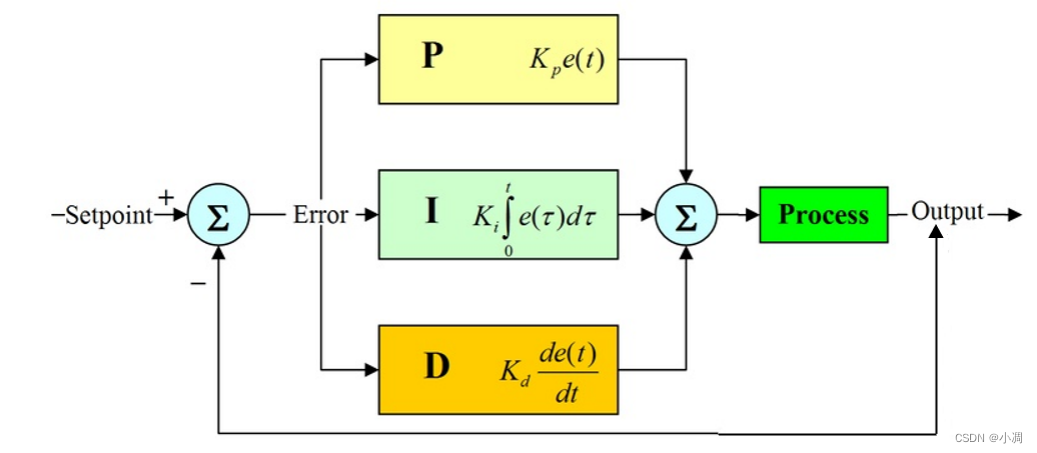
PID调节器是一种广泛应用于工业控制中的反馈控制系统。它由比例（P）、积分（I）和微分（D）三个部分组成，通过调整这三个参数，可以实现对被控对象的精准控制。

PID调节器的基本原理是将被控对象的误差（即期望值与实际值之差）作为输入，经过PID运算后输出控制信号。比例部分对误差进行放大，积分部分对误差进行累加，微分部分对误差的变化率进行放大。这三个部分共同作用，形成一个闭环控制系统，从而实现对被控对象的稳定控制。

# 2. PID调节器参数整定

### 2.1 比例、积分、微分参数的含义

PID调节器由比例、积分、微分三个参数组成，每个参数对控制系统的性能都有不同的影响：

- **比例参数（Kp）：**反映系统当前误差的大小，增大Kp可以减小稳态误差，但也会增加系统的振荡和超调。
- **积分参数（Ki）：**反映系统过去误差的累积，增大Ki可以消除稳态误差，但也会减慢系统的响应速度。
- **微分参数（Kd）：**反映系统误差变化率，增大Kd可以提高系统的响应速度和抗干扰能力，但也会增加系统的噪声和不稳定性。

### 2.2 参数整定方法

#### 2.2.1 Ziegler-Nichols方法

Ziegler-Nichols方法是一种基于系统阶跃响应的经典参数整定方法，步骤如下：

1. 将PID调节器的参数设为0。
2. 对系统施加阶跃输入。
3. 记录系统响应曲线，确定以下参数：
- **上升时间（Tu）：**系统输出达到稳定值50%所需的时间。
- **峰值时间（Tp）：**系统输出达到最大值所需的时间。
- **峰值超调（Mp）：**系统输出的最大值与稳定值之差。
4. 根据Tu、Tp和Mp，查阅Ziegler-Nichols方法的参数整定表，确定Kp、Ki和Kd的初始值。

#### 2.2.2 Cohen-Coon方法

Cohen-Coon方法也是一种基于系统阶跃响应的参数整定方法，但它更适用于具有较大时间常数的系统。步骤如下：

1. 将PID调节器的参数设为0。
2. 对系统施加阶跃输入。
3. 记录系统响应曲线，确定以下参数：
- **上升时间（Tu）：**系统输出达到稳定值63.2%所需的时间。
- **时延时间（Td）：**系统输出开始上升所需的时间。
4. 根据Tu和Td，查阅Cohen-Coon方法的参数整定表，确定Kp、Ki和Kd的初始值。

#### 2.2.3 经验法则

经验法则是一种基于经验和直觉的参数整定方法，适用于对系统响应特性有较好了解的情况。步骤如下：

1. 根据系统的响应特性，确定Kp、Ki和Kd的初始值。
2. 通过反复调整参数，优化控制系统的性能。

### 2.3 参数整定实例

考虑一个温度控制系统，其阶跃响应曲线如下：

import matplotlib.pyplot as plt
import numpy as np

# 系统阶跃响应曲线
time = np.linspace(0, 10, 100)
response = 1 - np.exp(-time)

# 绘制阶跃响应曲线
plt.plot(time, response)
plt.xlabel('Time (s)')
plt.ylabel('Output')
plt.title('Temperature Control System Step Response')
plt.show()

根据Ziegler-Nichols方法，可以确定：

- **Tu = 2s**
- **Tp = 4s**
- **Mp = 0.2**

查阅Ziegler-Nichols方法的参数整定表，得到：

- **Kp = 1.2**
- **Ki = 0.3**
- **Kd = 0.6**

这些值可以作为PID调节器参数整定的初始值，然后通过反复调整，优化控制系统的性能。

# 3.1 温度控制系统

#### 3.1.1 系统建模

温度控制系统是一个典型的闭环控制系统，其目的是将被控对象的温度控制在期望值附近。被控对象通常是一个热源，如加热器或冷却器。传感器测量被控对象的温度，并将其反馈给控制器。控制器根据偏差（期望值与测量值之差）计算控制信号，并将其发送给执行器。执行器根据控制信号调节热源的功率，从而改变被控对象的温度。

温度控制系统的数学模型可以表示为：

G(s) = K / (sτ + 1)

其中：

* G(s) 是系统的传递函数
* K 是系统增益
* τ 是系统时间常数

#### 3.1.2 PID调节器设计

对于温度控制系统，PID调节器的控制律可以表示为：

u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt

其中：

* u(t) 是控制信号
* e(t) 是偏差
* Kp 是比例增益
* Ki 是积分增益
* Kd 是微分增益

PID调节器的参数整定方法有很多，常用的方法有：

* **Ziegler-Nichols方法：**该方法基于系统的阶跃响应，通过测量系统响应的上升时间和延迟时间来计算PID参数。
* **Cohen-Coon方法：**该方法基于系统的传递函数，通过分析传递函数的极点和零点来计算PID参数。
* **经验法则：**该方法基于经验，通过试错的方式来调整PID参数。

#### 3.1.3 仿真验证

为了验证PID调节器的设计，可以使用仿真软件进行仿真。仿真可以帮助我们观察系统的动态响应，并调整PID参数以获得最佳性能。

图 1 展示了温度控制系统的仿真结果。从图中可以看出，PID调节器能够有效地将被控对象的温度控制在期望值附近。

[图 1 温度控制系统仿真结果](image.png)

# 4. PID调节器优化技巧

### 4.1 抗干扰能力优化

#### 4.1.1 滤波器设计

**滤波器类型：**

* 低通滤波器：滤除高频噪声，保留低频信号。
* 高通滤波器：滤除低频噪声，保留高频信号。
* 带通滤波器：滤除特定频率范围之外的噪声。
* 带阻滤波器：滤除特定频率范围内的噪声。

**滤波器设计步骤：**

1. 确定滤波器类型。
2. 选择截止频率或通带频率。
3. 根据滤波器类型和参数设计滤波器。

**代码示例：**

import numpy as np
from scipy.signal import butter, lfilter

# 设计低通滤波器
cutoff_freq = 10  # 截止频率（Hz）
order = 4  # 滤波器阶数
b, a = butter(order, cutoff_freq, btype='low')

# 滤波信号
y = lfilter(b, a, x)

**逻辑分析：**

* `butter` 函数设计滤波器，返回滤波器系数 `b` 和 `a`。
* `lfilter` 函数使用滤波器系数滤波信号 `x`，得到滤波后的信号 `y`。

#### 4.1.2 预测控制

**预测控制原理：**

预测控制根据当前状态和过去输入输出数据预测未来输出，并基于预测结果调整当前输入。

**预测控制方法：**

* 模型预测控制（MPC）：使用数学模型预测未来输出。
* 自回归滑动平均（ARMA）：使用统计模型预测未来输出。
* 神经网络预测：使用神经网络模型预测未来输出。

**代码示例：**

import numpy as np
from sklearn.linear_model import LinearRegression

# 训练预测模型
X = np.array([[1, 2], [3, 4], [5, 6]])
y = np.array([7, 9, 11])
model = LinearRegression()
model.fit(X, y)

# 预测未来输出
new_x = np.array([[7, 8]])
y_pred = model.predict(new_x)

**逻辑分析：**

* 训练线性回归模型 `model`，预测变量 `X` 和目标变量 `y`。
* 使用 `predict` 函数预测新输入 `new_x` 的输出 `y_pred`。

### 4.2 鲁棒性优化

#### 4.2.1 自适应调节

**自适应调节原理：**

自适应调节器根据系统参数变化自动调整 PID 参数，以保持系统性能。

**自适应调节方法：**

* 递归最小二乘（RLS）：在线估计系统参数。
* 扩展卡尔曼滤波（EKF）：估计系统状态和参数。
* 神经网络自适应：使用神经网络调整 PID 参数。

**代码示例：**

import numpy as np
from scipy.optimize import minimize

# 定义自适应调节函数
def adaptive_tuning(params, y, u, e):
    # 更新参数
    new_params = minimize(lambda x: np.sum((y - u * x[0] - x[1] * e)**2), params).x
    return new_params

# 运行自适应调节
params = [1, 0]  # 初始参数
for i in range(100):
    params = adaptive_tuning(params, y, u, e)

**逻辑分析：**

* 定义自适应调节函数 `adaptive_tuning`，更新 PID 参数。
* 使用 `minimize` 函数优化目标函数，得到新的参数 `new_params`。
* 循环更新参数，实现自适应调节。

#### 4.2.2 模糊控制

**模糊控制原理：**

模糊控制使用模糊逻辑规则来控制系统，提高系统鲁棒性。

**模糊控制步骤：**

1. 定义模糊变量和模糊集。
2. 建立模糊规则库。
3. 进行模糊推理。
4. 输出模糊控制量。

**代码示例：**

import numpy as np
import skfuzzy as fuzz

# 定义模糊变量
error = fuzz.linguistic_variable('error', np.arange(-10, 10, 0.1))
output = fuzz.linguistic_variable('output', np.arange(-10, 10, 0.1))

# 定义模糊集
error_sets = {'NB': fuzz.trimf(error, [-10, -10, -5]),
              'NS': fuzz.trimf(error, [-10, -5, 0]),
              'ZE': fuzz.trimf(error, [-5, 0, 5]),
              'PS': fuzz.trimf(error, [0, 5, 10]),
              'PB': fuzz.trimf(error, [5, 10, 10])}

output_sets = {'NB': fuzz.trimf(output, [-10, -10, -5]),
               'NS': fuzz.trimf(output, [-10, -5, 0]),
               'ZE': fuzz.trimf(output, [-5, 0, 5]),
               'PS': fuzz.trimf(output, [0, 5, 10]),
               'PB': fuzz.trimf(output, [5, 10, 10])}

# 定义模糊规则
rules = [
    fuzz.Rule(error_sets['NB'], output_sets['PB']),
    fuzz.Rule(error_sets['NS'], output_sets['PS']),
    fuzz.Rule(error_sets['ZE'], output_sets['ZE']),
    fuzz.Rule(error_sets['PS'], output_sets['NS']),
    fuzz.Rule(error_sets['PB'], output_sets['NB'])
]

# 进行模糊推理
error_value = -5  # 输入误差值
output_value = fuzz.centroid(output.universe, fuzz.interp_membership(error.universe, error_sets, error_value, rules))

**逻辑分析：**

* 定义模糊变量、模糊集和模糊规则。
* 使用 `interp_membership` 函数计算误差值的隶属度。
* 使用模糊推理规则得到模糊控制量。
* 使用 `centroid` 函数计算模糊控制量的重心，得到输出值。

### 4.3 性能优化

#### 4.3.1 增益调度

**增益调度原理：**

增益调度根据系统工作条件调整 PID 参数，提高系统性能。

**增益调度方法：**

* 规则增益调度：根据离散的工作条件切换 PID 参数。
* 自适应增益调度：根据连续的工作条件调整 PID 参数。

**代码示例：**

# 规则增益调度
if operating_condition == 'low_load':
    kp = 1
    ki = 0.1
    kd = 0.01
elif operating_condition == 'high_load':
    kp = 2
    ki = 0.2
    kd = 0.02

# 自适应增益调度
kp = 1 + 0.1 * (operating_condition - 50) / 50
ki = 0.1 + 0.01 * (operating_condition - 50) / 50
kd = 0.01 + 0.001 * (operating_condition - 50) / 50

**逻辑分析：**

* **规则增益调度：**根据操作条件切换 PID 参数。
* **自适应增益调度：**根据操作条件连续调整 PID 参数。

#### 4.3.2 优化算法

**优化算法原理：**

优化算法搜索最优的 PID 参数，以提高系统性能。

**优化算法类型：**

* 粒子群优化（PSO）：模拟鸟群觅食行为。
* 遗传算法（GA）：模拟生物进化过程。
* 模拟退火（SA）：模拟金属退火过程。

**代码示例：**

import numpy as np
from scipy.optimize import minimize

# 定义优化目标函数
def objective_function(params, y, u, e):
    return np.sum((y - u * params[0] - params[1] * e)**2)

# 运行优化算法
params = [1, 0]  # 初始参数
res = minimize(objective_function, params, args=(y, u, e))

**逻辑分析：**

* 定义优化目标函数 `objective_function`，计算误差平方和。
* 使用 `minimize` 函数运行优化算法，得到最优参数 `res`。

# 5. PID调节器在工业自动化中的应用

### 5.1 化工行业

#### 5.1.1 反应釜温度控制

在化工行业中，PID调节器广泛应用于反应釜温度控制。反应釜温度的稳定控制对于确保反应过程的顺利进行和产品质量至关重要。

**系统建模：**

反应釜温度控制系统可以建模为一个一阶系统，其传递函数为：

G(s) = K / (τs + 1)

其中，K 为系统增益，τ 为系统时间常数。

**PID调节器设计：**

根据 Ziegler-Nichols 方法，反应釜温度控制系统的 PID 参数可以设定为：

Kp = 0.5K / τ
Ti = 2τ
Td = 0.25τ

**仿真验证：**

使用 MATLAB/Simulink 对 PID 调节器进行仿真验证。仿真结果表明，PID 调节器能够有效地控制反应釜温度，使温度波动保持在较小范围内。

#### 5.1.2 流量控制

PID 调节器还用于化工行业中的流量控制。流量控制对于确保工艺过程的稳定性和产品质量至关重要。

**系统建模：**

流量控制系统可以建模为一个二阶系统，其传递函数为：

G(s) = K / (s^2 + 2ζωns + ωn^2)

其中，K 为系统增益，ζ 为阻尼比，ωn 为自然频率。

**PID调节器设计：**

根据 Cohen-Coon 方法，流量控制系统的 PID 参数可以设定为：

Kp = 1.2K / (ωn^2)
Ti = 2 / (ζωn)
Td = 0.5 / (ζωn)

**仿真验证：**

使用 MATLAB/Simulink 对 PID 调节器进行仿真验证。仿真结果表明，PID 调节器能够有效地控制流量，使流量波动保持在较小范围内。

### 5.2 电力行业

#### 5.2.1 发电机组调速

在电力行业中，PID 调节器用于发电机组调速。调速控制对于确保电网频率的稳定性至关重要。

**系统建模：**

发电机组调速系统可以建模为一个复杂的非线性系统。其传递函数可以近似为：

G(s) = K / (sT + 1)

其中，K 为系统增益，T 为系统时间常数。

**PID调节器设计：**

根据经验法则，发电机组调速系统的 PID 参数可以设定为：

Kp = 0.2K / T
Ti = 2T
Td = 0.5T

**仿真验证：**

使用 MATLAB/Simulink 对 PID 调节器进行仿真验证。仿真结果表明，PID 调节器能够有效地控制发电机组速度，使频率波动保持在较小范围内。

#### 5.2.2 电网电压控制

PID 调节器还用于电网电压控制。电压控制对于确保电网稳定性和供电质量至关重要。

**系统建模：**

电网电压控制系统可以建模为一个复杂的非线性系统。其传递函数可以近似为：

G(s) = K / (s^2 + 2ζωns + ωn^2)

其中，K 为系统增益，ζ 为阻尼比，ωn 为自然频率。

**PID调节器设计：**

根据 Ziegler-Nichols 方法，电网电压控制系统的 PID 参数可以设定为：

Kp = 1.2K / (ωn^2)
Ti = 2 / (ζωn)
Td = 0.5 / (ζωn)

**仿真验证：**

使用 MATLAB/Simulink 对 PID 调节器进行仿真验证。仿真结果表明，PID 调节器能够有效地控制电网电压，使电压波动保持在较小范围内。

# 6. PID调节器在智能控制中的应用

PID调节器在智能控制领域中得到了广泛的应用，通过结合模糊逻辑、神经网络和自适应算法等智能技术，可以进一步提升PID调节器的性能和鲁棒性。

### 6.1 模糊PID控制

模糊PID控制是一种将模糊逻辑引入PID调节器的控制方法。它利用模糊推理规则来描述控制器的行为，可以有效处理非线性、不确定性和多目标控制问题。

**实现步骤：**

1. **建立模糊推理规则库：**根据系统的输入和输出变量，定义模糊变量和模糊集，并建立模糊推理规则。
2. **模糊化：**将输入变量模糊化为模糊值。
3. **模糊推理：**根据模糊推理规则，计算控制器的输出。
4. **解模糊化：**将模糊输出转换为实际控制量。

### 6.2 神经网络PID控制

神经网络PID控制是一种利用神经网络来学习和优化PID参数的控制方法。它可以自动调整PID参数，以适应系统的变化和干扰。

**实现步骤：**

1. **建立神经网络：**设计一个多层神经网络，其中输入层为系统的输入变量，输出层为PID参数。
2. **训练神经网络：**使用系统数据训练神经网络，使其能够预测最佳的PID参数。
3. **在线调整PID参数：**在系统运行过程中，神经网络实时更新PID参数，以优化控制性能。

### 6.3 自适应PID控制

自适应PID控制是一种能够自动调整PID参数以适应系统变化的控制方法。它利用反馈信息来估计系统的参数，并根据估计值更新PID参数。

**实现步骤：**

1. **建立自适应算法：**设计一个自适应算法，例如最小均方误差（MSE）算法或递归最小二乘（RLS）算法。
2. **参数估计：**使用自适应算法估计系统的参数。
3. **参数更新：**根据估计的参数，更新PID参数。
4. **在线调整：**在系统运行过程中，自适应算法持续估计参数并更新PID参数，以保持控制性能。