【PyTorch中的门控循环单元（GRU）】：LSTM的高效替代方案

# 1. PyTorch与循环神经网络基础

## 1.1 PyTorch简介
在本章中，我们首先会对PyTorch框架进行概览，PyTorch已经成为机器学习尤其是深度学习研究中的首选工具之一。它因其动态计算图和用户友好的API而受到广泛欢迎，特别是在研究和实验性项目中。我们将简要介绍PyTorch的核心概念，如张量操作、自动微分系统以及数据加载和处理方法。

## 1.2 循环神经网络（RNN）的引入
接下来，我们会探讨循环神经网络（RNN），这是处理序列数据的神经网络类型之一。RNN能够处理任意长度的序列，并且能够捕获序列内的时间动态关系。我们将介绍RNN的基础概念，包括其在时间步上的递归应用，并且了解如何用PyTorch实现简单的RNN层。

## 1.3 PyTorch中的RNN实现
最后，本章将展示如何在PyTorch中实际构建RNN网络。我们将学习如何定义RNN模型、如何执行前向和后向传播，并且如何使用RNN进行基本的序列预测任务。通过动手实践，读者将掌握使用PyTorch处理序列数据的基本技能，并为进一步学习更高级的网络结构打下基础。

# 2. 理解门控循环单元（GRU）

### 2.1 GRU的理论基础
在这一小节中，我们将探讨GRU的理论基础，包括循环神经网络（RNN）的局限性和GRU的结构与特点。

#### 2.1.1 循环神经网络（RNN）的局限性
RNN（Recurrent Neural Networks）在处理序列数据方面表现出色，但由于其内部结构的限制，存在一些难以克服的挑战。在训练深度RNN时，梯度可能会消失或爆炸，这限制了网络的深度和学习能力。此外，RNN在处理长距离依赖问题时，也会遇到困难，因为随着时间的推移，信息可能会丢失或变得模糊不清。

RNN的这些问题催生了更高级的序列模型，如长短期记忆网络（LSTM）和门控循环单元（GRU）。这些模型通过引入门控机制来解决信息流动和长期依赖的问题。

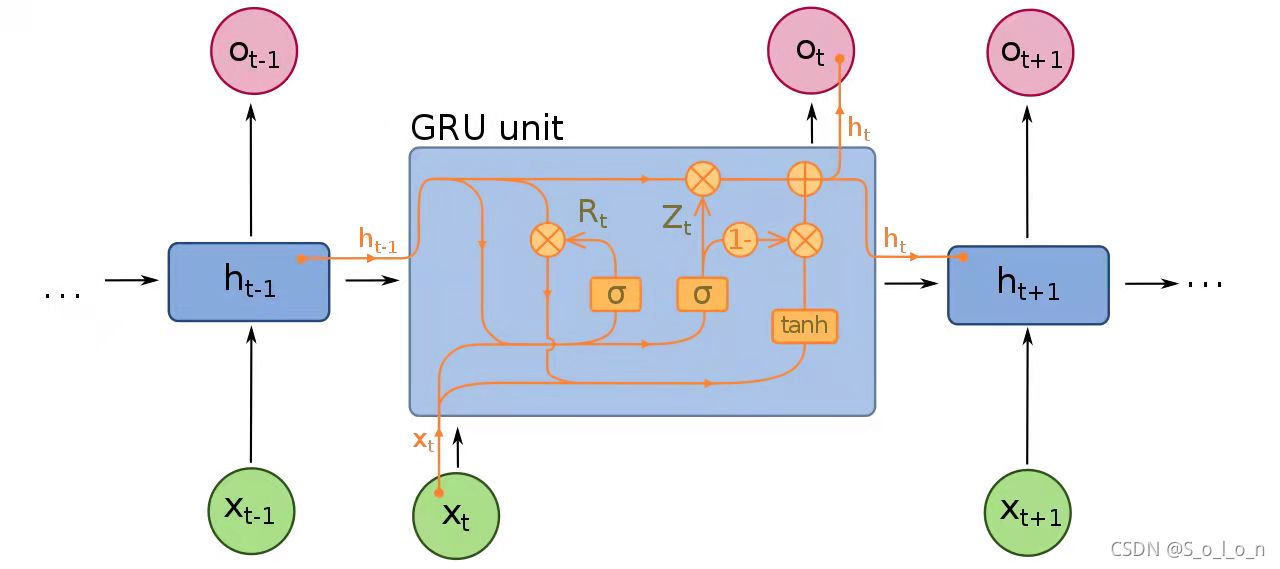
#### 2.1.2 GRU的结构与特点
GRU是一种相对较新的序列模型，旨在解决RNN的一些缺陷。GRU的核心创新在于其门控机制，通过合并更新门（update gate）和重置门（reset gate）来控制信息的流动。GRU比LSTM有更少的参数，这使得它在某些情况下能更快地训练。

GRU有以下两个主要组件：
- **重置门**（Reset Gate）：决定了多少过去的信息需要被忘记。
- **更新门**（Update Gate）：决定新输入的信息和先前的记忆单元有多大的比例被结合起来。

这些门控结构帮助GRU有效地解决了梯度消失和长距离依赖问题。接下来，让我们深入探讨GRU的工作原理。

### 2.2 GRU的工作原理

#### 2.2.1 重置门和更新门的作用
更新门和重置门是GRU中两个最重要的概念，它们通过门控机制来调整信息的流动。

- **更新门**的计算公式可以表示为：
$$ z_t = \sigma(W_z \cdot [h_{t-1}, x_t]) $$
其中，\( z_t \)是更新门在时间步 \( t \) 的输出，\( \sigma \) 是sigmoid函数，\( W_z \) 是更新门的权重矩阵，\( [h_{t-1}, x_t] \) 表示前一个隐藏状态和当前输入的连接。

- **重置门**的计算公式为：
$$ r_t = \sigma(W_r \cdot [h_{t-1}, x_t]) $$
其中，\( r_t \) 是重置门在时间步 \( t \) 的输出，\( W_r \) 是重置门的权重矩阵。

这两个门控制着信息的保留和遗忘，以及新信息和旧记忆的结合。

#### 2.2.2 候选隐藏状态与最终隐藏状态的计算
GRU的隐藏状态更新由候选隐藏状态和最终隐藏状态决定。候选隐藏状态 \( \tilde{h}_t \) 是未经过滤的新候选状态，最终隐藏状态 \( h_t \) 是根据更新门来决定保留多少历史信息。

- **候选隐藏状态**计算公式为：
$$ \tilde{h}_t = \tanh(W \cdot [r_t * h_{t-1}, x_t]) $$
其中，\( W \) 是权重矩阵，\( r_t * h_{t-1} \) 表示重置门与上一个隐藏状态的元素级乘积，\( x_t \) 是当前输入。

- **最终隐藏状态**计算公式为：
$$ h_t = (1 - z_t) * h_{t-1} + z_t * \tilde{h}_t $$
这里，\( z_t \) 决定了保留多少先前的隐藏状态 \( h_{t-1} \)，而 \( (1 - z_t) \) 和 \( z_t \) 确定了新候选状态 \( \tilde{h}_t \) 的加入比例。

通过这种方式，GRU能够灵活地在序列中传递信息，同时避免了梯度消失和爆炸的问题。

### 2.3 GRU与LSTM的比较

#### 2.3.1 LSTM的简化模型分析
LSTM通过引入输入门（input gate）、遗忘门（forget gate）和输出门（output gate）来控制信息的流动。与GRU相比，LSTM结构更为复杂，参数更多。

LSTM的内部状态和隐藏状态更新通过以下公式进行：
- 遗忘门：\( f_t = \sigma(W_f \cdot [h_{t-1}, x_t]) \)
- 输入门：\( i_t = \sigma(W_i \cdot [h_{t-1}, x_t]) \)
- 候选状态：\( \tilde{C}_t = \tanh(W_C \cdot [h_{t-1}, x_t]) \)
- 内部状态：\( C_t = f_t * C_{t-1} + i_t * \tilde{C}_t \)
- 输出门：\( o_t = \sigma(W_o \cdot [h_{t-1}, x_t]) \)
- 隐藏状态：\( h_t = o_t * \tanh(C_t) \)

LSTM通过复杂的门控制机制更精细地管理状态的更新，但也因此更难以训练。

#### 2.3.2 GRU的优势与应用场景
GRU由于其简化的设计，在许多任务中能够与LSTM媲美，甚至在某些情况下更胜一筹。由于GRU参数更少，训练更快，同时在许多基准测试中展现出与LSTM相似或更好的性能。GRU特别适合于数据量较少或者需要快速训练的场景。

在选择使用GRU还是LSTM时，应考虑具体任务、数据集大小和可用资源。对于需要高效训练和部署的场合，GRU往往是一个不错的选择。

我们已经学习了GRU的理论基础和工作原理，并与LSTM进行了比较。在下一章中，我们将探讨如何在PyTorch中实现GRU，以及如何训练和优化它。

# 3. PyTorch中的GRU实现

在第二章中，我们深入了解了GRU的理论基础和工作原理，并与LSTM进行了比较，揭示了GRU在不同应用场景中的优势。现在，让我们将焦点转向实践中如何在PyTorch中实现GRU，并通过构建模型、优化训练过程以及进行案例分析来具体应用它。

## 3.1 PyTorch GRU层的构建

### 3.1.1 GRU层的参数设置

在PyTorch中，实现GRU层是相当直接的，主要通过`torch.nn.GRU`类进行。GRU层有很多参数，它们