数据结构的深层探索：贪心算法的数学基础与证明

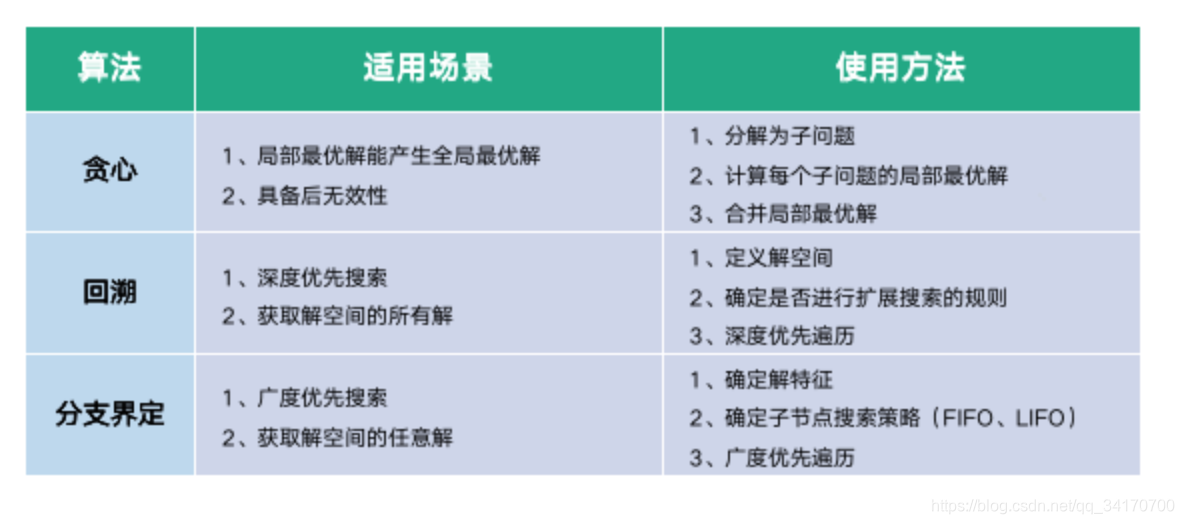
# 1. 贪心算法概述与应用场景

在计算机科学和数学优化领域，贪心算法是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的算法策略。贪心算法并不保证会得到最优解，但是其简单高效的特点使其在特定问题中非常受欢迎。

## 1.1 贪心算法的基本概念

贪心算法的核心思想是构建问题的解决方案时，采取局部最优解以期望构建出全局最优解。每一步选择都基于当前已有的信息做出最优决策，且一旦决策完成，就不会再回溯去改变。

## 1.2 贪心算法的适用场景

贪心算法适用于那些具有“贪心选择性质”的问题，即局部最优解能决定全局最优解。这类问题通常可以分为两大类：区间问题和选择问题。常见的应用场景包括哈夫曼编码、活动选择问题、最小生成树和最短路径等。

通过了解贪心算法的工作原理和适用范围，我们可以更好地理解其在实际问题中的应用。接下来章节将进一步探讨贪心算法背后的数学基础和策略构建。

# 2. 贪心算法的数学基础

贪心算法是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的算法。其核心在于，每一步都选取当前最优解，以期望得到全局最优解。为了深入理解贪心算法的工作原理和数学本质，本章将介绍贪心算法所依赖的基础数学概念，最优化理论，以及贪心选择性质。

## 2.1 基础数学概念

### 2.1.1 集合论基础

在数学领域，集合论是研究集合及其关系的基本理论。贪心算法的许多概念都可以归结为集合的操作与性质。例如，问题的解空间可以看作是解的集合，贪心算法的每一步选择都是在对这个集合进行操作。在求解贪心问题时，我们常常需要确定问题的可行解集合以及最优解的集合特性。下面是集合论中几个基础概念的简介：

- **集合**：集合是由不同元素组成的整体，每个元素称为集合的成员。
- **子集**：如果集合B中的每个元素都在集合A中，那么B是A的子集。
- **幂集**：集合A的幂集是指包含A的所有子集的集合。
- **笛卡尔积**：两个集合A和B的笛卡尔积是所有可能的有序对(a, b)，其中a属于A且b属于B。

### 2.1.2 证明技术

证明技术是贪心算法中不可或缺的一部分，通过数学证明我们能够确保算法的正确性。在贪心算法设计中常用的证明技术包括归纳法和反证法。

#### 归纳法

归纳法证明主要通过以下两个步骤进行：

1. **基础步骤**：证明问题对于某个初始情况是成立的。
2. **归纳步骤**：假设对某个具体的k，问题的结论成立，然后证明在此假设下，对于k+1，结论也成立。

通过归纳法，我们可以逐步证明贪心算法在每个阶段都是正确的，从而保证最终解的正确性。

#### 反证法

反证法是通过假设贪心算法得出的结论不正确，然后导出矛盾来证明算法的正确性。具体步骤如下：

1. 假设通过贪心算法得到的解不是最优解。
2. 推导出基于这个假设的矛盾。
3. 如果能成功地导出矛盾，说明假设不成立，即算法得到的解是正确的。

通过运用这些证明技术，我们可以确保贪心策略的正确性，并在理论上得到坚实的支撑。

## 2.2 最优化理论

### 2.2.1 最优化问题定义

最优化问题是指在给定的约束条件下，寻找最优解的问题。最优解可以是最小化或最大化某些目标函数的解。贪心算法经常用于求解这一类问题。

最优化问题可以一般化表示为：

- 目标函数：\( f(x_1, x_2, ..., x_n) \)
- 约束条件：\( g_j(x_1, x_2, ..., x_n) \leq b_j \) 或 \( g_j(x_1, x_2, ..., x_n) = b_j \)
- 决策变量：\( x_1, x_2, ..., x_n \)

最优化问题的目标是找到决策变量的一组值，使得目标函数值最优，同时满足所有的约束条件。

### 2.2.2 最优化问题的分类

最优化问题的分类有助于我们更好地理解和应用贪心算法。根据目标函数和约束条件的不同，最优化问题可以分为：

- **线性规划问题**：目标函数和约束条件均为线性的最优化问题。
- **整数规划问题**：决策变量必须为整数的最优化问题。
- **组合优化问题**：涉及组合结构，如集合、序列或图的最优化问题。

贪心算法在这些问题中的应用通常比其他算法（如动态规划）在时间复杂度上有优势，但不一定能得到全局最优解。

## 2.3 贪心选择性质

### 2.3.1 选择性质的数学描述

贪心选择性质指的是，在问题的最优解中，存在一组选择，这些选择是局部最优的，且可以构成全局最优解。用数学语言描述如下：

设问题P的最优解包含子问题P'的最优解，若贪心策略在P'中总是选择局部最优解，则称这种策略具有贪心选择性质。

### 2.3.2 贪心选择与最优解的关系

贪心选择性质的存在，是我们使用贪心算法解决最优化问题的信心来源。但是，并不是所有具有贪心选择性质的问题都能保证通过贪心算法得到全局最优解。因此，研究贪心选择性质与最优解的关系至关重要。

理论上，当满足以下两个条件时，贪心算法能够保证得到全局最优解：

1. **最优子结构**：一个问题的最优解包含了其子问题的最优解。
2. **贪心选择性质**：局部最优选择能产生全局最优解。

此外，贪心选择性质的证明通常需要展示算法的每一步选择都能够直接或间接地推动问题向着全局最优解的方向前进。

以上是第二章内容的概览，接下来我们