数据结构优化：贪心算法在资源分配中的角色

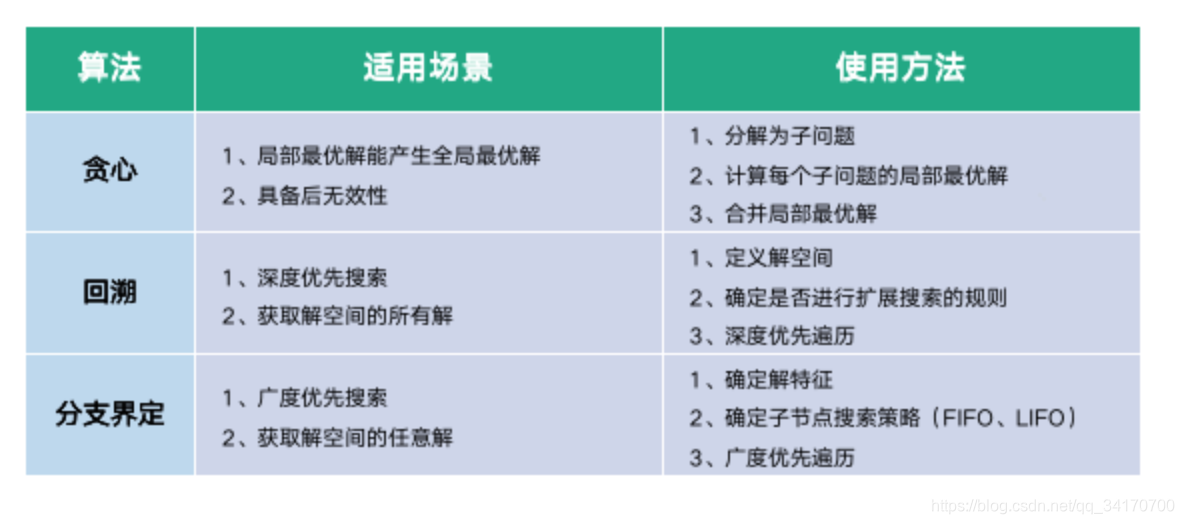
# 1. 贪心算法的基本原理

在算法的世界中，贪心算法是一类简单却强大的策略，它在求解优化问题时，总是选择当前看来最优的选择，希望这样能导致全局最优解。这种算法的核心是局部最优解的连贯性，即局部最优解能够构成全局最优解。

## 算法概述

贪心算法的基本思想非常直观，它不考虑整个问题的最优解，只关注在当前步骤中取得最优的结果，以此反复进行选择，直到问题得到解决。虽然贪心算法的正确性并不总是得到保证，但它在很多情况下能够提供高效的解决方案，特别是在满足贪心选择性质的问题中，它可以给出最优解。

## 理论与实践

在理论层面，贪心算法的选择必须满足贪心选择性质和最优子结构这两个条件。在实际应用中，贪心算法可用于解决各种优化问题，如调度问题、哈夫曼编码、图的最小生成树等。尽管贪心算法的每个局部选择都是最优的，但这并不意味着它总能找到全局最优解。因此，深入理解贪心算法的基本原理对于判断其适用性至关重要。

# 2. 贪心算法的理论基础与实践

## 2.1 贪心选择性质的探索

### 2.1.1 选择性质的定义和意义

贪心选择性质是指在求解优化问题时，通过局部最优选择能够导致全局最优解的一种属性。在贪心算法中，我们每一步都做出在当前看来最好的选择，也就是说，我们总是做出局部最优解，期望通过局部最优解来构造全局最优解。

对于贪心算法来说，选择性质是其理论基础的核心所在。如果没有贪心选择性质，贪心算法可能无法保证获得最优解。例如，对于旅行推销员问题，贪心策略并不能保证找到最短的环游路径，因为局部最优的选择可能会导致全局的非最优解。

### 2.1.2 算法的正确性分析

在贪心算法中，正确性分析通常通过证明局部最优解能够导出全局最优解来完成。正确性分析的一个关键点是证明算法的每一步选择都不会影响最终解的质量。

通常有以下几种方法来证明贪心算法的正确性：

1. **数学归纳法**：通过归纳的方式，假设在第k步之前贪心选择是正确的，然后证明第k步的贪心选择不会破坏前面步骤的正确性，从而推断出最终解的正确性。

2. **反证法**：假设贪心算法没有得到最优解，然后通过逻辑推理找出矛盾，从而证明假设不成立，贪心算法能够得到最优解。

3. **构造法**：直接构造出一种情况，展示贪心选择如何导致最终的全局最优解。

以上方法可以单独使用，也可以结合使用来增强证明的可靠性。

## 2.2 贪心策略在算法设计中的应用

### 2.2.1 贪心策略的分类和比较

贪心策略可以分为多种类型，常见的有最小生成树问题中的Kruskal算法和Prim算法、单源最短路径问题中的Dijkstra算法等。这些算法虽然解决的问题不同，但都遵循了贪心策略的共同原则。

在比较不同贪心策略时，主要从以下几个维度进行考量：

1. **时间复杂度**：算法执行的速度，即算法操作数和时间消耗。
2. **空间复杂度**：算法在执行过程中所占用的内存空间。
3. **适用范围**：算法所能解决的问题类型和适用的场景。
4. **实现复杂度**：算法的实现难度和编码工作量。

### 2.2.2 贪心策略与其他算法的结合

贪心算法通常与其他算法策略相结合，以获得更好的性能。例如，在解决图的最短路径问题时，Dijkstra算法是贪心策略的经典应用，但是在存在负权边的图中，Dijkstra算法无法找到最短路径，此时可以结合Bellman-Ford算法。

另一种结合方式是将贪心策略与动态规划结合，动态规划在全局考虑问题的同时，也可以采用贪心策略来简化问题的求解过程。

## 2.3 贪心算法的实例分析

### 2.3.1 经典问题：背包问题的贪心解法

背包问题是一类组合优化问题，其目标是选择一些物品，使得所选物品的总价值最大，同时不超过背包的承重限制。贪心算法在解决分数背包问题时非常有效，其核心是按照单位价值从高到低的顺序选择物品，即`价值/重量`比率最高的物品优先。

以下是一个简单的背包问题的贪心解法的Python代码实现：

def fractional_knapsack(value, weight, capacity):
    # 创建一个列表，存储物品的单位价值
    value_per_weight = [v / w for v, w in zip(value, weight)]
    # 将物品按照单位价值进行排序
    sorted_items = sorted(zip(value, weight, value_per_weight), key=lambda x: x[2], reverse=True)
    total_value = 0
    w = capacity
    # 遍历排序后的物品列表
    for v, w, vp_w in sorted_items:
        if w <= capacity:
            # 如果物品可以完整地装入背包，就将其全部装入
            capacity -= w
            total_value += v
        else:
            # 如果物品不能完整装入，就装入一部分
            total_value += v * (capacity / w)
            break
    return total_value

# 示例
values = [60, 100, 120]
weights = [10, 20, 30]
capacity = 50
max_value = fractional_knapsack(values, weights, capacity)
print(f"Maximum value we can obtain = {max_value}")

### 2.3.2 实际应用案例：调度算法中的贪心策略

在实际应用中，贪心算法常被用于调度问题，例如银行柜员分配问题、CPU调度问题等。在CPU调度中，贪心算法可以根据不同的标准（如最短作业优先、最高响应比优先）来决定下一个被处理的作业。

一个常见的调度算法应用是**最早截止时间优先（Earliest Deadline First，EDF）**策略。在这种策略中，任务按照截止时间从早到晚的顺序排列，每次选择截止时间最早的未处理任务进行处理。

以下是EDF策略的Python代码实现示例：

from heapq import heappop, heappush

class Task:
    def __init__(self, name, deadline):
        self.name = name
        self.deadline = deadline
    def __lt__(self, other):
        return self.deadline < other.deadline

def schedule_tasks(tasks):
    task_que