贪心算法与数据结构结合：探索问题求解的多样性

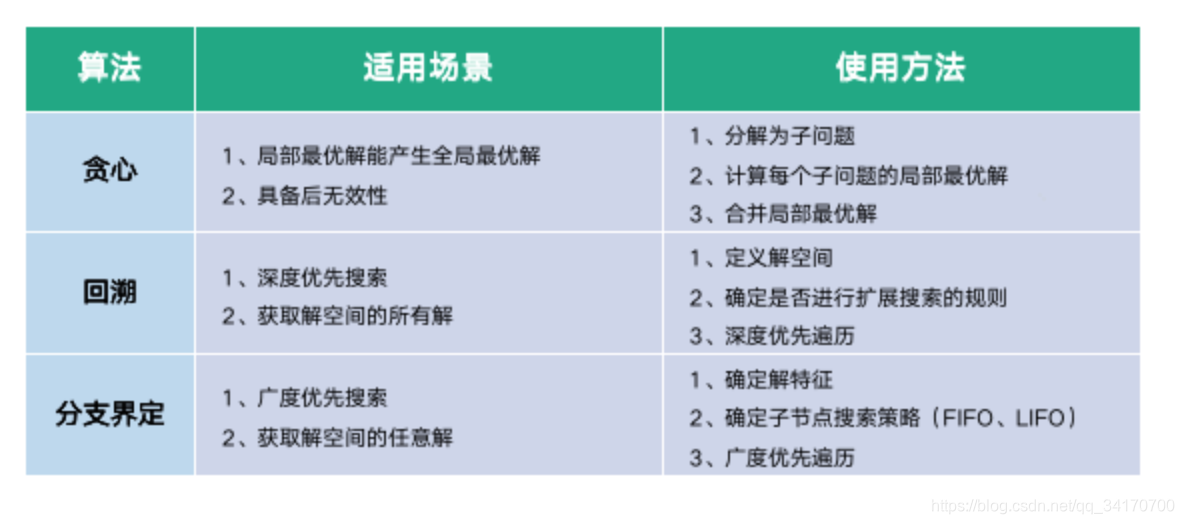
# 1. 贪心算法与数据结构简介

在本章中，我们将概述贪心算法和数据结构的基础知识，为深入理解这些概念打下坚实的基础。首先，我们会简单介绍贪心算法的特点以及它的应用场景。贪心算法是一种在每一步选择中都采取在当前状态下最好或最优的选择，从而希望导致结果是全局最好或最优的算法。

## 1.1 贪心算法简介

贪心算法在许多优化问题中扮演着关键角色，例如图论中的最小生成树，或者排序和搜索算法中的优化。它通常用于求解问题的最优解，尤其当问题表现出贪心选择性质，即局部最优解能决定全局最优解时。尽管贪心算法简单且高效，但并不是所有问题都能通过贪心算法得到最优解。

## 1.2 数据结构的作用

数据结构是组织和存储数据的一种方式，以便于可以高效地访问和修改。贪心算法在解决问题时，需要依赖合适的数据结构来高效管理数据，例如在任务调度中使用优先队列来管理任务的优先级，或是在图搜索中使用堆优化路径查找过程。本章会简要介绍数据结构在贪心算法中的应用，为后续章节中更深入的讨论做好铺垫。

# 2. 贪心算法的理论基础

### 2.1 贪心算法的概念与原理

#### 2.1.1 贪心算法的定义

贪心算法是一种在每一步选择中都采取在当前状态下最好或最优（即最有利）的选择，从而希望导致结果是全局最好或最优的算法。贪心算法并不保证会得到最优解，但是在某些问题中贪心算法的解就是最优解。

在实际应用中，贪心算法常常被用于解决优化问题，尤其是当问题具有“贪心选择性质”时。贪心选择性质指的是局部最优选择能决定全局最优。需要注意的是，贪心算法通常需要结合问题的具体情况来设计贪心策略，并通过证明来确保算法的正确性。

#### 2.1.2 贪心选择性质

贪心选择性质是指一个问题的整体最优解可以通过一系列局部最优的选择来构成。也就是说，当进行每一步的决策时，都选取当前情况下的最优解，而这些局部最优解能够组合成全局最优解。

例如，在一个背包问题中，如果每次总是选择重量最轻但价值最高的物品放入背包，直到背包无法再装下更多的物品，这种策略就利用了贪心选择性质，因为每一步都做出了当前最优的选择。

#### 2.1.3 最优子结构概念

最优子结构是指一个问题的最优解包含其子问题的最优解。在贪心算法中，如果问题具有最优子结构，那么通过每一步贪心选择构造的解将导致最终解是全局最优的。

举例来说，最小生成树问题就具有最优子结构。如果我们能够找到一个图的最小生成树，那么从这个最小生成树中移除任意一条边都不会得到另一个最小生成树。这意味着，通过贪心策略（每次选择最小权重的边）找到的最小生成树一定是全局最优解。

### 2.2 贪心算法的策略分析

#### 2.2.1 贪心策略的分类

贪心策略有多种分类方法，常见的有以下几种：
- **构造法**：通过逐步构造最终解的方式来进行选择，如构造哈夫曼树进行数据压缩。
- **优化法**：通过局部优化达到全局最优，如Dijkstra算法寻找最短路径。
- **规划法**：通过建立模型预测最优路径，如贪心算法解决多机调度问题。

在每一种策略中，都需要根据问题的具体情况来确定贪心的选择方式，以保证贪心策略能够有效地工作。

#### 2.2.2 策略选择的标准

选择合适的贪心策略通常依赖于问题的结构特点。以下是一些判断策略是否适用的标准：
- **贪心选择是否导致最优解**：要确保所采用的贪心策略能够保证最终得到最优解。
- **子问题的独立性**：子问题的解不会相互影响，贪心选择后不会影响其他子问题的解。
- **子问题的最优子结构**：子问题的解可以直接构成原问题的解。

#### 2.2.3 实例分析：活动选择问题

活动选择问题是贪心算法的经典应用案例，问题描述如下：有n个活动，每个活动有一个开始时间和结束时间。我们的目标是选择最大数量的互不相交的活动。

活动选择问题的贪心策略是按照活动的结束时间进行排序，然后从前往后选择活动，每次选择结束时间最早的未进行的活动。这样可以保证在完成一个活动后，能够留下尽可能多的时间给其它活动，从而最大化选择的活动数量。

# Python 代码示例：活动选择问题

def activity_selection(activities):
    # 对活动按结束时间进行排序
    activities.sort(key=lambda x: x[1])
    # 选择的第一个活动
    last_finish_time = activities[0][1]
    selected_activities = [activities[0]]
    # 对每个活动进行遍历
    for i in range(1, len(activities)):
        # 如果当前活动的开始时间大于等于上一个被选择活动的结束时间
        if activities[i][0] >= last_finish_time:
            selected_activities.append(activities[i])
            last_finish_time = activities[i][1]
    return selected_activities

# 示例数据
activities = [(1, 4), (3, 5), (0, 6), (5, 7), (3, 9), (5, 9), (6, 10), (8, 11), (8, 12), (2, 14), (12, 16)]

# 执行活动选择算法
result = activity_selection(activities)
print("Selected activities:", result)

通过该代码，我们可以选择最大数量的互不相交的活动。这只是一个简单的例子，贪心算法的实际应用场景和优化可能更加复杂，但核心思想是相同的。

# 3. 数据结构在贪心算法中的应用

## 3.1 栈和队列的贪心应用

### 3.1.1 栈在贪心算法中的作用

栈是一种后进先出（Last In First Out, LIFO）的数据结构，它在贪心算法中的主要作用体现在其能够追踪一系列操作，并在需要时能够快速逆转操作的顺序。在贪心算法中，栈可以用于维护当前状态，以便我们可以回溯到之前的最优决策点。例如，在解决表达式求值、括号匹配等问题时，栈是一个非常有用的工具。

### 3.1.2 队列的适用场景分析

与栈不同，队列是一种先进先出（First In First Out, FIFO）的数据结构。队列在贪心算法中的应用通常与处理多个候选元素有关，如在任务调度、事件处理等领域。队列使得算法能够按照到达的顺序处理元素，保证了公平性和顺序性，这对于某些贪心策略是非常重要的。

### 3.1.3 栈和队列的案例研究

一个经典的应用栈的贪心算法的例子是括号匹配问题。在这个问题中，算法需要验证一个由圆括号`()`、花括号`{}`和方括号`[]`组成的字符串是否匹配正确。栈可以用来跟踪每个开括号，并在遇到相应类型的闭括号时将其弹出。

def is_parentheses_balanced(expression):
    stack = []
    parentheses_map = {')': '(', '}': '{', ']':