深度剖析AUC：复杂模型中的计算与应用技巧

# 1. AUC的基本概念和重要性

在现代数据科学和机器学习领域，AUC（Area Under the Curve）是一个不可或缺的评价指标，它衡量了分类器在所有可能的阈值下的性能。AUC的值介于0到1之间，1表示完美预测，而0.5表示随机猜测。在多类别或不平衡数据集上，AUC能够提供比精确度更为全面和公正的性能评估。

AUC之所以重要，是因为它不仅考虑了模型的分类准确性，也考虑了其预测概率的排序能力。尤其在医疗诊断、金融欺诈检测等领域，AUC成为了评估预测模型性能的关键指标。此外，AUC为比较不同模型提供了一个共同的尺度，不受样本分布的影响，是交叉验证的理想选择。

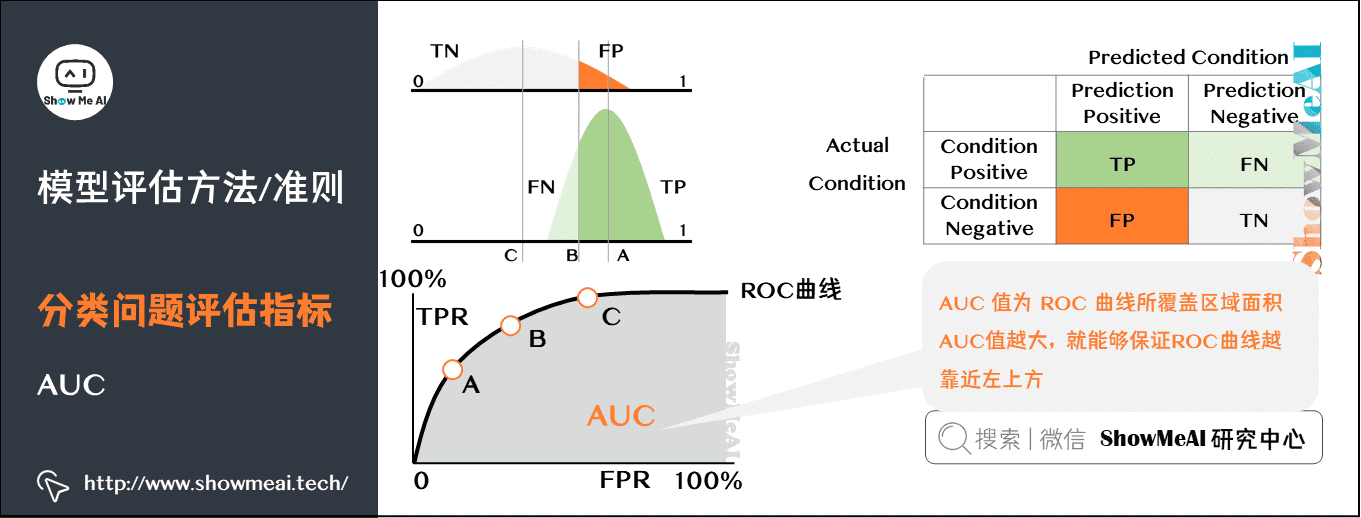
理解AUC的关键在于掌握其背后的ROC（Receiver Operating Characteristic）曲线，它以真正率（True Positive Rate, TPR）和假正率（False Positive Rate, FPR）为坐标轴，展现了在不同阈值下的分类性能。在接下来的章节中，我们将深入探讨AUC的理论基础、计算方法和优化技巧。

# 2. AUC的理论基础

## 2.1 AUC的定义和计算方法

### 2.1.1 AUC的基本定义
AUC（Area Under Curve）是评估分类模型性能的一种指标，特别是在处理不平衡数据集时，AUC显得尤为重要。它代表了在所有可能的正负样本对中，正样本被模型赋予更高分数的概率。简单来说，AUC衡量的是模型区分正负样本的能力。

AUC的取值范围在0到1之间。一个随机猜测的分类器的AUC值为0.5，而一个完美分类器的AUC值为1。因此，AUC值越高，模型的性能越好。

### 2.1.2 AUC的计算方法和步骤
AUC的计算是基于ROC曲线（Receiver Operating Characteristic curve）。ROC曲线是通过绘制不同阈值下的真正率（True Positive Rate, TPR）和假正率（False Positive Rate, FPR）来绘制的。计算AUC的基本步骤如下：

1. 计算每个样本的预测概率，并根据概率对样本进行排序。
2. 遍历每个可能的阈值，对于每个阈值，计算TPR和FPR。
3. 在TPR和FPR坐标系中，连接各点形成ROC曲线。
4. 使用梯形法则或积分计算曲线下的面积，即得到AUC值。

from sklearn.metrics import roc_curve, auc
import matplotlib.pyplot as plt

# 假设y_true为真实的标签，y_scores为模型预测的概率
fpr, tpr, thresholds = roc_curve(y_true, y_scores)
roc_auc = auc(fpr, tpr)

# 绘制ROC曲线
plt.figure()
plt.plot(fpr, tpr, color='darkorange', lw=2, label='ROC curve (area = %0.2f)' % roc_auc)
plt.plot([0, 1], [0, 1], color='navy', lw=2, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver Operating Characteristic')
plt.legend(loc="lower right")
plt.show()

### 2.2 AUC的理论解释

#### 2.2.1 AUC与ROC曲线的关系
AUC实际上就是ROC曲线下的面积，因此，理解了ROC曲线，也就理解了AUC。ROC曲线能够直观地表示出模型在不同阈值下的性能表现，而AUC则是一个综合的指标，将ROC曲线下的面积量化为一个单一的值，从而方便模型性能的比较。

#### 2.2.2 AUC的理论意义和应用价值
AUC是评估模型性能的一个无量纲指标，不受数据不平衡的影响，因此它在诸如信用卡欺诈检测、疾病诊断等不平衡数据集的分类问题中尤其有用。AUC的高值意味着模型更擅长区分正负样本，因此在实际应用中，AUC常常作为一个关键指标来衡量模型是否可以部署到生产环境。

AUC的理论意义在于它提供了一个评估模型性能的全局视角，而不仅仅是某一个特定阈值的表现。这在模型选择和优化过程中尤为重要，因为它帮助决策者从宏观上理解模型的预测能力。在应用价值方面，AUC可以辅助我们选择最佳的分类模型，尤其是在需要在多个模型间进行比较时，AUC成为一个非常有力的评估工具。

# 3. AUC的计算技巧

## 3.1 AUC的直接计算技巧
### 3.1.1 直接计算AUC的方法
在模型评估中，直接计算AUC（Area Under the Curve）通常涉及到统计分析中的非参数检验方法。为了直接计算AUC，我们首先要根据模型的预测概率值对样本进行排序，然后计算真正率（True Positive Rate, TPR）和假正率（False Positive Rate, FPR）随阈值变化的曲线，最后将这个曲线下的面积积分出来。在实际操作中，我们使用不同的阈值来划分正负样本，并记录每个阈值下的真正例（True Positives, TP）、假正例（False Positives, FP）、真负例（True Negatives, TN）和假负例（False Negatives, FN）的数量。通过对这些数量进行计算，我们可以得到一系列的TPR和FP