【Java机器学习算法库：主成分分析（PCA）详解】：数据降维技术的秘密武器

# 1. 主成分分析（PCA）概述

主成分分析（PCA）是一种被广泛采用的降维技术，其核心目的是通过线性变换将高维数据转换到低维空间，同时尽可能保留数据的重要特征。PCA在数据处理、特征提取和模式识别等领域中扮演着关键角色。尽管PCA通常被认为是数据预处理的一部分，但它的实际应用远不止于此，它同样能够帮助我们揭示数据的基本结构，甚至可以用于数据分析和可视化。

在实际应用中，PCA通过寻找数据集中的主成分——这些主成分是数据变异性的主要来源——来实现降维。这个过程涉及到识别数据集中的主要趋势和模式，进而生成一组新的、不相关的特征，这些新特征被称为主成分。值得注意的是，主成分是按照解释数据变异性的顺序排列的，第一主成分解释了最大方差，而后续的每个主成分则解释了剩余变异中最大的那部分。

虽然PCA是一种强大的工具，但它也有其局限性，比如它在处理非线性关系或对异常值敏感等方面存在缺陷。因此，在使用PCA之前，了解其理论基础和潜在的局限性至关重要。接下来的章节将详细探讨PCA的数学原理、实际应用案例，以及如何优化和扩展PCA的使用。

# 2. PCA的数学基础和理论

## 2.1 向量空间和基变换

### 2.1.1 向量与空间的定义

向量是多维空间中的一个基础概念，是一个有大小和方向的量。在数学和物理学中，向量不仅被用来表示物理量，如速度、加速度、力等，也被广泛应用于计算机科学中的图形学、数据处理等领域。

在数学中，一个n维向量可以表示为一个由n个有序数（或称为分量）组成的数组，通常写成一个行向量或列向量的形式。例如，一个三维空间的向量可以表示为:

\[
\vec{v} = \begin{bmatrix} v_1 \\ v_2 \\ v_3 \end{bmatrix}
\]

或

\[
\vec{v} = [v_1, v_2, v_3]
\]

向量空间是线性代数中的核心概念之一，它是由向量构成的集合，并且满足加法和数乘的封闭性。向量空间的定义包括向量加法和标量乘法的基本运算规则，从而可以对向量进行线性组合、线性相关和线性独立等性质的分析。

### 2.1.2 基变换与坐标变换

在向量空间中，基向量是构成空间的一组线性无关的向量，任何空间中的向量都可以由这组基向量线性组合得到。基变换是一种非常重要的数学工具，用于在不同的坐标系统之间进行转换。

假设我们有两组基 \(\{ \vec{e_1}, \vec{e_2}, ..., \vec{e_n} \}\) 和 \(\{ \vec{e'_1}, \vec{e'_2}, ..., \vec{e'_n} \}\)，向量 \(\vec{v}\) 在这两组基下的表示分别是 \(x_1, x_2, ..., x_n\) 和 \(x'_1, x'_2, ..., x'_n\)。基变换的目标就是找到一个变换矩阵 \(P\)，使得：

\[
\begin{bmatrix}
x'_1 \\
x'_2 \\
\vdots \\
x'_n
\end{bmatrix}
=
P \times
\begin{bmatrix}
x_1 \\
x_2 \\
\vdots \\
x_n
\end{bmatrix}
\]

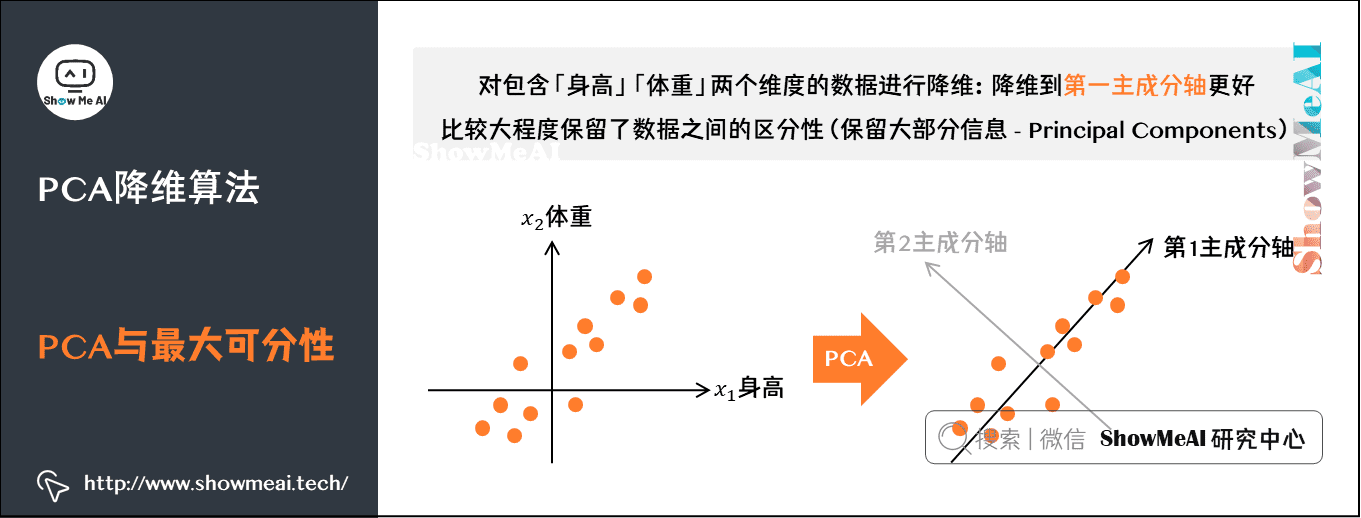
变换矩阵 \(P\) 由新基向量相对于旧基向量的表示构成。在PCA中，基变换用来找到数据的主成分，即寻找新的坐标轴，使得数据在此坐标轴上的方差最大。

## 2.2 协方差矩阵和特征分解

### 2.2.1 协方差矩阵的推导

在统计学中，协方差是衡量两个随机变量相关程度的度量。对于一组随机变量 \(X = \{x_1, x_2, ..., x_n\}\)，协方差矩阵是一个表示各变量间协方差的方阵。

假设有一个数据集，每一行代表一个观测值，每一列代表一个变量。协方差矩阵 \(C\) 可以通过下面的公式计算得到：

\[
C = \frac{1}{n-1} (X - \overline{X})^T (X - \overline{X})
\]

其中，\(X\) 是一个 \(n \times m\) 的矩阵，\(n\) 是观测值的数量，\(m\) 是变量的数量，\(\overline{X}\) 是数据集的平均值矩阵。

### 2.2.2 特征值与特征向量的计算

特征值与特征向量是线性代数中的重要概念，对于任何方阵 \(A\)，如果存在非零向量 \(\vec{v}\) 和标量 \(\lambda\) 满足方程 \(A\vec{v} = \lambda\vec{v}\)，则称 \(\lambda\) 是矩阵 \(A\) 的一个特征值，\(\vec{v}\) 是对应于 \(\lambda\) 的一个特征向量。

在PCA中，我们通常对协方差矩阵进行特征分解，以找到数据的主成分。计算步骤大致如下：

1. 计算数据的协方差矩阵 \(C\)。
2. 计算协方差矩阵的特征值和特征向量。
3. 将特征值按从大到小排序。
4. 对应于最大特征值的特征向量是第一个主成分，依次类推。

特征向量的方向指示了数据变化最大的方向，特征值的大小则表明了数据在该特征向量方向上的方差大小。

## 2.3 主成分的选取和解释

### 2.3.1 主成分的选取标准

主成分分析（PCA）的核心目的是通过线性变换将原始数据转换到一组线性不相关的变量上，这些新变量称为主成分。选取主成分的标准通常基于以下两个方面：

1. **方差解释比例**：每个主成分都是原始数据协方差矩阵的一个特征向量，对应的特征值表示了该主成分所解释的数据方差大小。选取主成分时，我们倾向于选择那些具有较大特征值的主成分，因为它们能够解释更多的数据变异性。通常，我们会选择累积贡献率达到一定阈值（例如85%）的主成分。

2. **特征值的大小**：特征值越大，表示该主成分所解释的数据方差越多，因此，我们会优先考虑那些特征值较大的主成分。

### 2.3.2 主成分的解释和意义

每个主成分都可以看作是从原始数据中提取出的一个新特征，且这些新特征是相互独立的。第一个主成分捕获了数据中最大的方差方向，第二个主成分与第一个主成分正交，并捕获了剩余方差中最大的方向，依此类推。

理解主成分的意义可以帮助我们了解数据的内在结构和模式。例如，在图像识别领域，前几个主成分通常能够捕捉到图像的主要特征，如轮廓、纹理等。在金融数据分析中，主成分可能与某些经济指标或者市场因素相关联，从而帮助我们理解数据背后的经济学原理。

主成分分析不仅仅是一种数据降维的工具，更是一种从高维数据中提取信息、发现数据内部结构的有效方法。通过PCA，我们可以将复杂的数据结构简化为少数几个具有代表性的特征，这在数据分析、模式识别和机器学习中具有重要的应用价值。

# 3. Java机器学习算法库中的PCA实现

在现代数据科学与机器学习中，利用现成的算法库可以大大提高开发效率，对于PCA（主成分分析）这一强大的降维技术也不例外。Java在企业级应用中非常流行，因此存在许多优秀的Java机器学习库。在这一章节中，我们将探讨如何在Java环境中实现PCA，并逐步深入到具体的编码实现和结果解释。

## 3.1 算法库介绍与环境搭建

在开始使用PCA之前，首先要熟悉可用的Java机器学习库，并搭建相应的开发环境。Java生态中的机器学习库众多，下面将介绍一些常用的库和环境搭建步骤。

### 3.1.1 常用的Java机器学习库

在众多Ja