【卷积神经网络的反向传播】：深入理解梯度下降算法

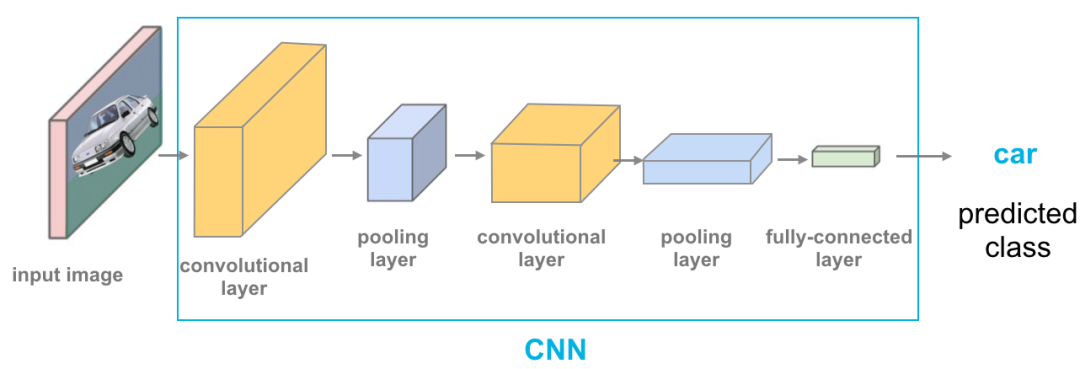
# 1. 卷积神经网络基础知识

## 1.1 卷积神经网络的起源与定义

卷积神经网络（Convolutional Neural Networks，CNNs）是深度学习领域中最为成功的算法之一，尤其在图像识别和处理领域取得了突破性的成就。CNNs的灵感来源于生物学中视觉皮层的处理机制，它能够自动且有效地从图像中提取特征。CNN通过卷积层、池化层等构建，这些层能够逐层学习数据的高级特征，是目前图像识别和分类任务中的核心技术。

## 1.2 CNN的基本结构

CNN的基本结构通常包括卷积层、激活函数、池化层和全连接层。卷积层通过多个可学习的滤波器（或称为卷积核）提取输入数据的空间特征。激活函数如ReLU（Rectified Linear Unit）引入非线性因素，使得网络能够学习复杂的模式。池化层进一步减少数据的空间尺寸，降低计算量和防止过拟合。全连接层则在特征提取完成后，进行分类等决策任务。

from keras.models import Sequential
from keras.layers import Conv2D, MaxPooling2D, Flatten, Dense

# 构建一个简单的CNN模型
model = Sequential()
model.add(Conv2D(32, (3, 3), activation='relu', input_shape=(64, 64, 3)))
model.add(MaxPooling2D(pool_size=(2, 2)))
model.add(Flatten())
model.add(Dense(10, activation='softmax'))

在上述代码中，我们用Keras框架构建了一个简单的CNN模型，其中包含了卷积层、池化层和全连接层。

## 1.3 CNN在实际中的应用

CNN被广泛应用于图像和视频识别、图像分类、医学图像分析、自然语言处理等多个领域。它在自动驾驶汽车中的视觉系统、医学图像的病理分析，甚至在股票市场数据的预测等方面都显示出了巨大的潜力。CNN能够自动学习数据中的层次性特征，极大地减少了对人工特征工程的需求。

在理解CNN的基础知识后，下一章我们将深入探讨反向传播算法的理论框架，这是理解神经网络训练过程中的关键一步。

# 2. 反向传播算法的理论框架

## 2.1 神经网络中的梯度下降

### 2.1.1 梯度下降的基本概念

梯度下降是优化算法的核心，尤其在神经网络训练中扮演着关键角色。它是一种迭代优化算法，通过不断调整模型参数，以最小化损失函数。梯度下降的核心思想是沿着损失函数下降最快的方向（梯度的反方向）进行参数更新。

在数学上，假设有一个损失函数 $L(w)$，我们的目标是找到参数 $w$ 的最优值，使得 $L(w)$ 最小。梯度向量指向函数增长最快的方向，因此可以通过以下更新规则来不断逼近最小值：

$$ w := w - \eta \nabla L(w) $$

其中，$\eta$ 是学习率，控制着我们前进的步长，$\nabla L(w)$ 是损失函数 $L$ 关于参数 $w$ 的梯度。

### 2.1.2 梯度下降的优化算法

尽管基本的梯度下降算法易于实现且直观，但在实际应用中，它可能会遇到若干挑战，如收敛速度慢、陷入局部最小值等问题。因此，研究者们提出了多种优化算法来克服这些问题。

**动量法**通过引入动量概念来加速梯度下降，减少参数更新的振荡。其核心思想是利用历史梯度信息帮助加速梯度下降，特别是在梯度方向频繁变化的优化问题中表现出色。

$$ v_t = \gamma v_{t-1} + \eta \nabla L(w_t) $$
$$ w_{t+1} = w_t - v_t $$

其中，$v_t$ 是在时间 $t$ 的速度，$\gamma$ 是动量系数。

**自适应学习率算法**，例如Adagrad、RMSprop和Adam，能够根据参数的历史梯度信息自动调整每个参数的学习率。这使得模型能够更加快速且稳健地收敛。Adagrad算法会累积过去梯度的平方，RMSprop对Adagrad的累积过程进行了修正，而Adam则结合了RMSprop的平方梯度估计和动量法的思想。

## 2.2 反向传播算法的工作原理

### 2.2.1 错误信号的传递

反向传播算法是梯度下降算法在神经网络中的具体实现，其核心在于计算损失函数关于每个参数的梯度。反向传播的过程可以分为两个阶段：前向传播和反向传播。

在前向传播阶段，输入信号经过每一层的加权求和和激活函数的处理后传递到下一层，直至最后一层，产生预测输出和损失值。反向传播阶段则是从输出层开始，逐层向前计算损失函数相对于网络参数的梯度。

每一层的梯度计算依赖于其上一层的梯度，这样误差信号就像波浪一样从输出层向输入层传播，故得名反向传播算法。

### 2.2.2 权重和偏置的更新规则

反向传播计算出的梯度，能够指导我们如何更新神经网络中的权重和偏置，以减小预测值与真实值之间的差异。权重和偏置的更新遵循梯度下降的原理，即按照梯度的反方向更新参数。

更新公式如下：

$$ w_{\text{new}} = w_{\text{old}} - \eta \frac{\partial L}{\partial w} $$

$$ b_{\text{new}} = b_{\text{old}} - \eta \frac{\partial L}{\partial b} $$

其中，$w$ 和 $b$ 分别表示权重和偏置，$\eta$ 表示学习率，$\frac{\partial L}{\partial w}$ 和 $\frac{\partial L}{\partial b}$ 表示损失函数 $L$ 关于权重和偏置的梯度。

在实际应用中，为了减少梯度消失和梯度爆炸问题，可能需要结合使用正则化技术，如L2正则化和Dropout等。

## 2.3 反向传播中的数学基础

### 2.3.1 链式法则在反向传播中的应用

链式法则是求导的一个基本法则，它允许我们将复合函数的导数分解为内函数和外函数导数的乘积。在反向传播中，链式法则被用来高效地计算梯度，特别是在涉及多层网络的情况下。

假设有一个多层的神经网络，其中每个节点的输出由一个激活函数 $g$ 控制，其输入由前一层的输出加权求和得到，权重为 $w$。如果损失函数 $L$ 可以表示为输出节点的函数，那么损失函数关于权重 $w$ 的梯度可以通过链式法则计算得到：

$$ \frac{\partial L}{\partial w} = \frac{\partial L}{\partial y} \frac{\partial y}{\partial z} \frac{\partial z}{\partial w} $$

其中，$y$ 表示激活函数的输出，$z$ 表示加权求和的结果。通过这种方式，我们可以从前向传播过程中传递的信号中提取每个参数对最终输出的影响。

### 2.3.2 矩阵运算与梯度计算

在实际的神经网络实现中，大量的数据和参数处理都通过矩阵运算来完成。这种矩阵运算的效率很高，尤其是在使用GPU进行并行计算时。梯度的计算也依赖于矩阵运算，这使得整个反向传播过程可以在硬件层面得到优化。

例如，对于一个简单的全连接层，假设输入向量 $x$，权重矩阵 $W$ 和偏置向量 $b$，输出向量 $y$ 可以表示为：

$$ y = Wx + b $$

使用矩阵运算表示反向传播中的梯度计算如下：

$$ \frac{\partial L}{\partial W} = \frac{\partial L}{\partial y} \frac{\partial y}{\partial W} = \frac{\partial L}{\partial y} x^T $$

$$ \frac{\partial L}{\partial b} = \frac{\partial L}{\partial y} \frac{\partial y}{\partial b} = \frac{\partial L}{\partial y} $$

这里，$x^T$ 表示 $x$ 的转置。矩阵运算为我们提供了一种简洁的方法来描述和计算梯度，使得网络的训练过程更加高效。

在接下来的章节中，我们将深入了解反向传播算法在卷积神经网络中的应用细节，以及一些实际的优化策略。

# 3. 反向传播算法在卷积神经网络中的应用

## 3.1 卷积层的反向传播

### 3.1.1 卷积操作的梯度计算

在卷积神经网络（CNN）中，卷积层是特征提取的核心组件。为了深入理解如何在卷积层中应用反向传播算法，我们需要探讨卷积操作的梯度计算。卷积操作的梯度计算与传统的全连接网络中的梯度计算有所不同，这主要是由于卷积操作的局部连接和权重共享特性。

卷积操作的梯度计算主要涉及以下几个步骤：
1. **计算梯度误差**：反向传播开始于损失函数对卷积层输出的梯度。这个梯度误差是通过链式法则反向传播到卷积层的。
2. **处理权重共享**：由于卷积核在输入特征图上滑动并共享相同的权重，我们需要对所有相关位置的梯度进行累加，以计算出每个卷积核的梯度。
3. **边界效应处理**：在处理边缘像素时，由于卷积核不能完全覆盖输入特征图的边缘，因此需要特别处理，通常是通过填充（padding）或裁剪（cropping）等技术。

以下是处理卷积层反向传播时的一个代码示例（假设使用PyTorch框架）：

def conv_backward(d_input, weight, stride, padding, input_size):
    # d_input 是损失函数相对于卷积层输出的梯度
    # weight 是卷积层的权重
    # stride 是卷积操作的步长
    # padding 是卷积操作的填充参数
    # input_size 是输入特征图的尺寸
    kernel_size = weight.size(2)
    d_weight = torch.zeros_like(weight)  # 初始化权重梯度
    d_input_unpadded = d_input[:, :, padding:-padding, padding:-padding]  # 移除边界填充

    for i in range(d_input_unpadded.size(2)):
        for j in range(d_input_unpadded.size(3)):
            d_weight += d_input_unpadded[:, :, i, j:i+kernel_size].unsqueeze(3) * \
                        input[:, :, i*stride:i*stride+kernel_size, j:j+kernel_size].unsqueeze(2)
    d_weight /= d_input.siz