从理论到应用：MATLAB线性回归分析的完全攻略

# 1. MATLAB线性回归基础理论

在开始讨论MATLAB中线性回归的具体实现之前，我们首先要了解线性回归作为一种统计学方法的基础理论。线性回归旨在通过一个线性模型来量化两个或多个变量之间的关系。在最简单的情况下，线性回归被用来预测连续值的因变量 Y，基于一个或多个自变量 X。

## 1.1 线性回归的基本概念

线性回归模型通常可以表示为 Y = a + bX + ε，其中 Y 是因变量，X 是自变量，a 和 b 是模型参数，ε 表示误差项。目标是通过数据点来估计 a 和 b 的值，使得模型的预测尽可能接近实际观测值。

## 1.2 线性回归模型的类型

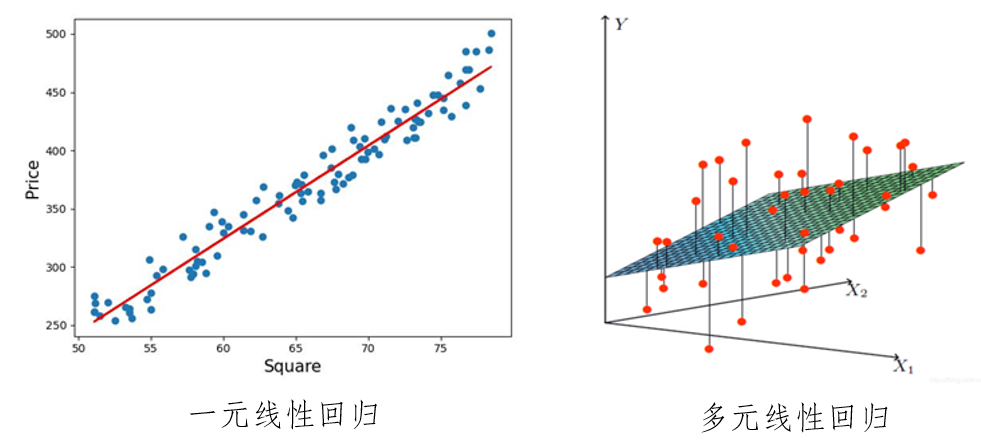
根据自变量的数量，线性回归可以分为简单线性回归（一个自变量）和多元线性回归（多个自变量）。简单线性回归侧重于找出一个解释变量与因变量之间的关系，而多元线性回归则可以处理多个解释变量的影响。

在下一章节中，我们将探讨如何使用MATLAB内置的函数和工具箱来进行线性回归分析，并详细讨论多元线性回归模型的建立和评估。

# 2. MATLAB中的线性回归实现

## 2.1 MATLAB线性回归函数介绍

### 2.1.1 线性回归函数概述

MATLAB提供了多种用于线性回归分析的函数，这些函数可以让用户轻松地实现从数据的初步分析到模型构建、评估和预测的整个流程。在MATLAB中，最常用的线性回归函数包括`fitlm`，它用于执行多元线性回归分析。此外，`regress`和`stepwiselm`函数也提供了高级回归分析功能，它们分别支持一般线性模型的参数估计和逐步回归方法。

### 2.1.2 使用内置函数进行简单线性回归

简单线性回归分析是研究两个变量之间的线性关系，其中一个是自变量（解释变量），另一个是因变量（响应变量）。在MATLAB中，我们可以使用`fitlm`函数快速地进行简单线性回归分析。

以下是使用`fitlm`函数进行简单线性回归分析的代码示例：

% 假设X和Y是已经准备好的自变量和因变量的数据向量
X = [1, 2, 3, 4, 5];  % 示例数据，实际应用中应使用真实数据
Y = [2.1, 3.9, 6.1, 8.0, 10.2];  % 示例数据，实际应用中应使用真实数据

% 使用fitlm函数进行简单线性回归分析
lm = fitlm(X, Y);

% 显示回归模型的详细结果
disp(lm);

执行这段代码后，MATLAB会输出线性回归模型的详细统计信息，包括回归系数、R方值、F统计量、t统计量等。这些统计量可以帮助我们评估模型的拟合优度和每个系数的显著性。

## 2.2 多元线性回归分析

### 2.2.1 多元线性回归模型的建立

多元线性回归模型是研究一个因变量与多个自变量之间线性关系的统计方法。在MATLAB中，多元线性回归模型的建立通常使用`fitlm`函数，它能够处理包含多个预测变量的线性模型。

以下是一个多元线性回归分析的示例：

% 假设A是一个m*n的数据矩阵，其中m是观测数，n是变量数，包括一个因变量和多个自变量
% Y是一个m*1的数据向量，表示m个观测的因变量值

% 生成示例数据
A = randn(100, 4);  % 100个观测，4个变量
Y = A(:,1) + 2*A(:,2) + A(:,3) + randn(100, 1);  % 假设的真实模型加上一些随机噪声

% 添加一个常数项，以便模型可以估计截距
A = [ones(100, 1) A];

% 使用fitlm函数进行多元线性回归分析
lm = fitlm(A, Y);

% 显示回归模型的详细结果
disp(lm);

### 2.2.2 参数估计与假设检验

参数估计是确定模型中每个自变量对应系数的过程。在多元线性回归模型中，我们通常关注每个系数的估计值、标准误差、t统计量、p值等统计量，以判断每个自变量对因变量的影响是否显著。

以下是多元线性回归模型参数估计和假设检验的分析：

% 访问线性模型中的系数估计
coefficients = lm.Coefficients.Estimate;

% 访问标准误差
std_errors = lm.Coefficients.SE;

% 访问t统计量和p值
t_statistics = lm.Coefficients.tStat;
p_values = lm.Coefficients.pValue;

% 输出参数估计和假设检验结果
fprintf('回归系数估计值：\n');
disp(coefficients);
fprintf('标准误差：\n');
disp(std_errors);
fprintf('t统计量：\n');
disp(t_statistics);
fprintf('p值：\n');
disp(p_values);

### 2.2.3 模型的诊断与优化

在建立多元线性回归模型之后，需要对模型进行诊断，确保模型的有效性和可靠性。模型诊断的目的是发现模型的潜在问题，如非线性、异方差性、多重共线性等问题。

MATLAB中可以使用`plotResiduals`函数绘制残差图，帮助识别模型中的问题：

% 绘制残差图诊断模型
figure;
plotResiduals(lm);

如果发现模型存在问题，我们可以尝试通过变量转换、添加交互项或使用正则化方法等手段对模型进行优化。

## 2.3 线性回归中的模型评估

### 2.3.1 拟合优度的检验

拟合优度的检验是评估线性回归模型与实际观测数据拟合程度的重要方法。在MATLAB中，我们可以使用决定系数（R^2）来衡量模型的拟合优度。R^2值越接近1，表示模型拟合得越好。

以下是如何在MATLAB中计算并解释R^2值的示例代码：

% 计算R^2值
r_squared = lm.Rsquared.Ordinary;

% 输出R^2值
fprintf('模型的决定系数（R^2）：%.3f\n', r_squared);

### 2.3.2 预测精度的评估方法

模型的预测精度评估是决定模型是否可以在实际中使用的另一项重要指标。常用的预测精度评估方法包括均方误差（MSE）、均方根误差（RMSE）和平均绝对误差（MAE）。

以下是计算并展示这些预测精度指标的MATLAB代码：

% 使用模型进行预测
predicted_Y = predict(lm, A);

% 计算MSE、RMSE和MAE
mse = mean((Y - predicted_Y).^2);
rmse = sqrt(mse);
mae = mean(abs(Y - predicted_Y));

% 输出评估结果
fprintf('均方误差（MSE）：%.3f\n', mse);
fprintf('均方根误差（RMSE）：%.3f\n', rmse);
fprintf('平均绝对误差（MAE）：%.3f\n', mae);

通过这些指标的计算，我们可以对线性回归模型的预测性能进行量化评估，进而决定模型是否满足实际应用的需求。

# 3. MATLAB线性回归实战演练

## 实际数据的线性回归分析
### 数据的导入与处理
在进行线性回归分析前，关键的一步是数据的准备。数据导入与处理阶段，涉及到数据的清洗、预处理、转换等环节。在这个部分，我们需要确保数据集的质量，保证其符合线性回归分析的要求。MATLAB提供了一系列函数来帮助用户完成这些任务，例如`readtable`用于导入数据，`clean`用于清洗数据，`impute`用于填补缺失值。

要导入数据，可以使用以下命令：

% 假设数据存储在Excel文件中
filename = 'data.xlsx';
data = readtable(filename);

紧接着，我们进行数据预处理，比如检查缺失值：

% 检查数据中的缺失值
misData = ismissing(data);

并根据需要处理它们，比如删除含有缺失值的行：

% 删除缺失值所在行
data(misData, :) = [];

接下来，我们需要对数据进行必要的转换。例如，如果数据中包含分类变量，我们需要将其转换为适合线性回归模型的格式，比如使用虚拟变量（dummy variables）。

% 假设